CS231A Lecture 7:Multi-view geometry (1)
Reading:
[HZ] Chapter 10 “3D reconstruction of cameras and structure”
[HZ] Chapter 18 “N-view computational methods”
[HZ] Chapter 19 “Auto-calibration”
[FP] Chapter 13 “projective structure from motion”
[Szelisky] Chapter 7 “Structure from motion”
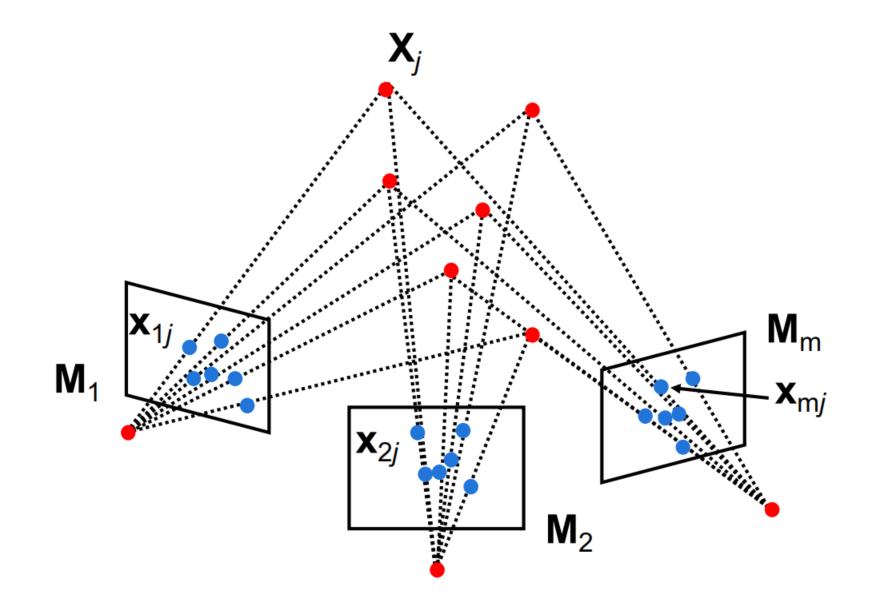
The SFM problem
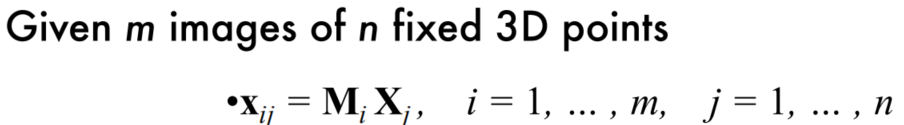

Affine SFM
Affine structure from motion(simpler problem)
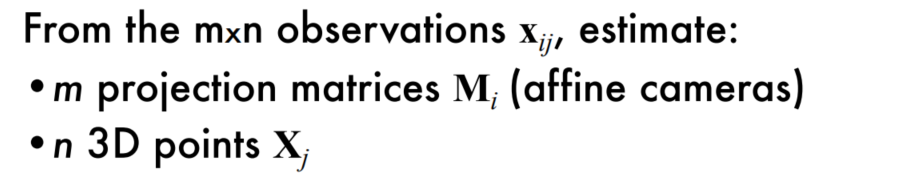
Perspective vs Affine
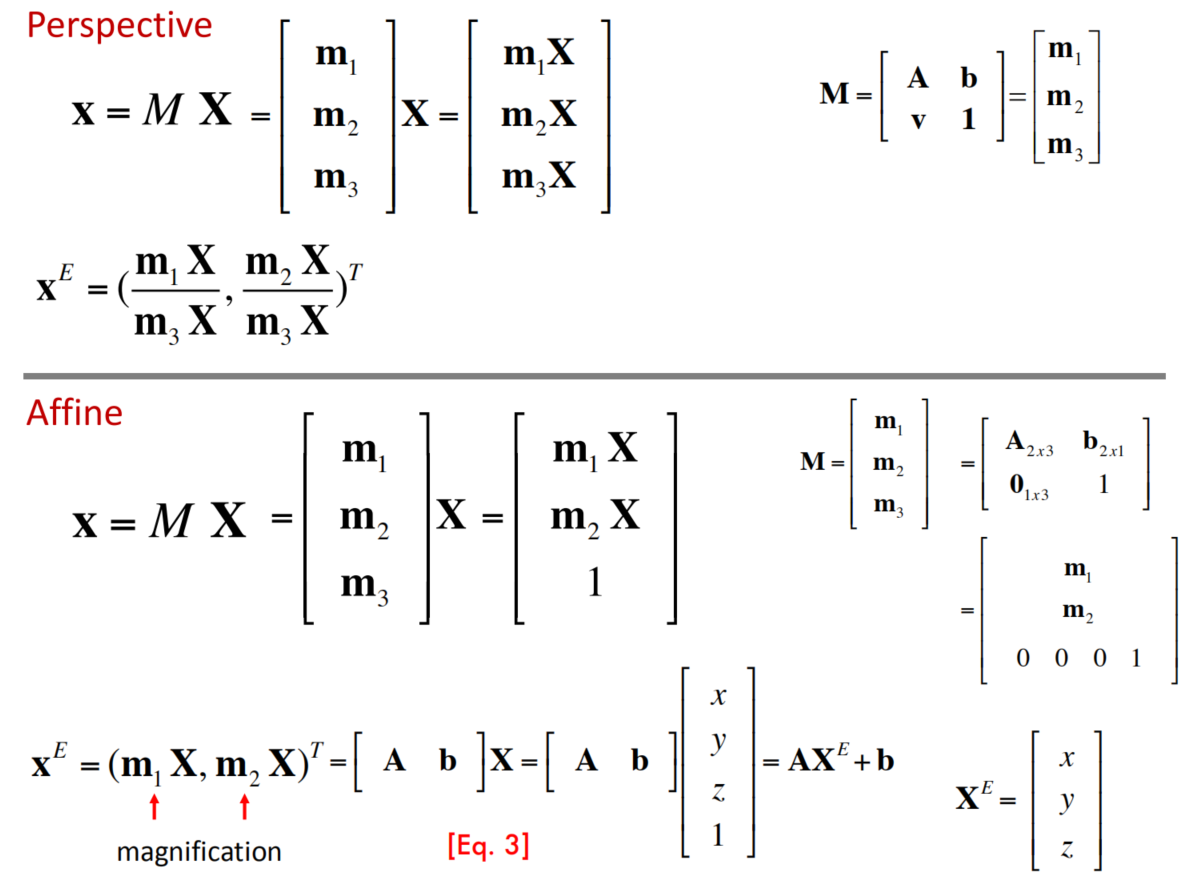
Affine cameras
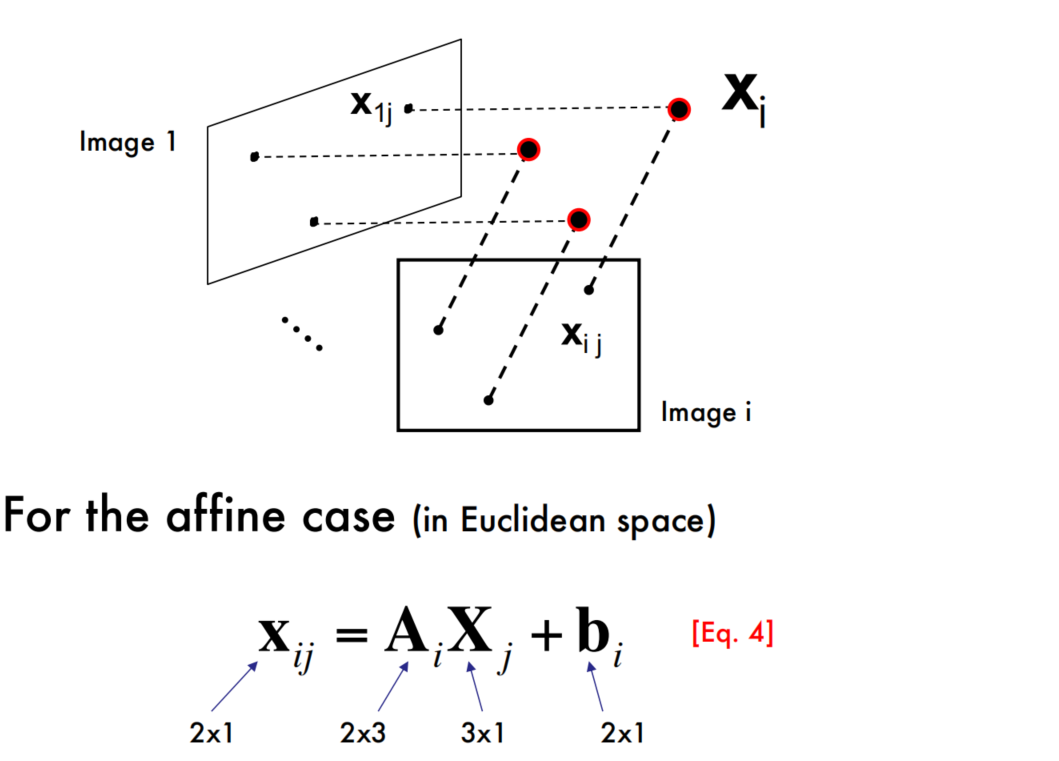
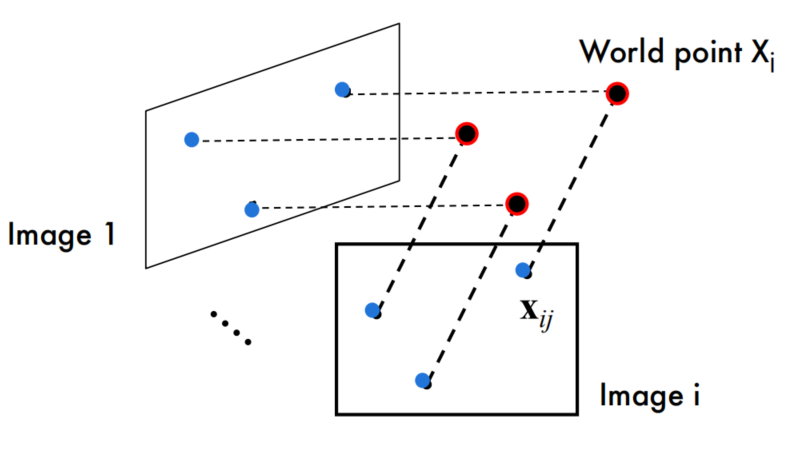
The Affine Structure-from-Motion Problem


思考:
这里乍一看是只知道$x_{ij}$,要求等式右边的三个未知量,看起来解不出来。
不过把这里的对应关系理清楚就可以理解了,$x_{ij}$是$X_j$在第$i$张图上的投影,而$A_i$和$b_i$是构成对应第$i$张图的投影矩阵$M_i$。
并且,这里每一个$x_{ij}$能提供2个等式,即$\begin{cases} &m_1X_j = x_{ij}[0] \\ &m_2X_j=x_{ij}[1] \end{cases}$,总共可以有$2m\times n$个等式;
而$M_i$有8个未知量,而$X_j$有3个未知量,总共要求解的未知量数目为$8m+3n-8$个。
因此,这个等式在一定情况下是可以求解的。
疑问
Q:为什么未知量的数目是$8m+3n-8$呢?这个$-8$是如何来的?
A:我认为这里应该是有一帧图像的投影矩阵是已知的,比如假定第一帧图象是在世界坐标系原点拍摄的,或者假定已知世界坐标系与相机坐标系在某一帧下的关系,就可以得到这帧的投影矩阵;不然的话,可能找不出一个合适的初始值来求解这个方程组,或者可能这个方程组有无穷个解,而我们需要的只是一个有现实意义(比如指定了世界坐标系)的解。
A factorization method –Tomasi & Kanade algorithm
C. Tomasi and T. KanadeShape and motion from image streams under orthography: A factorization
method. IJCV, 9(2):137-154, November 1992.
Data centering
Centering: subtract the centroid of the image points
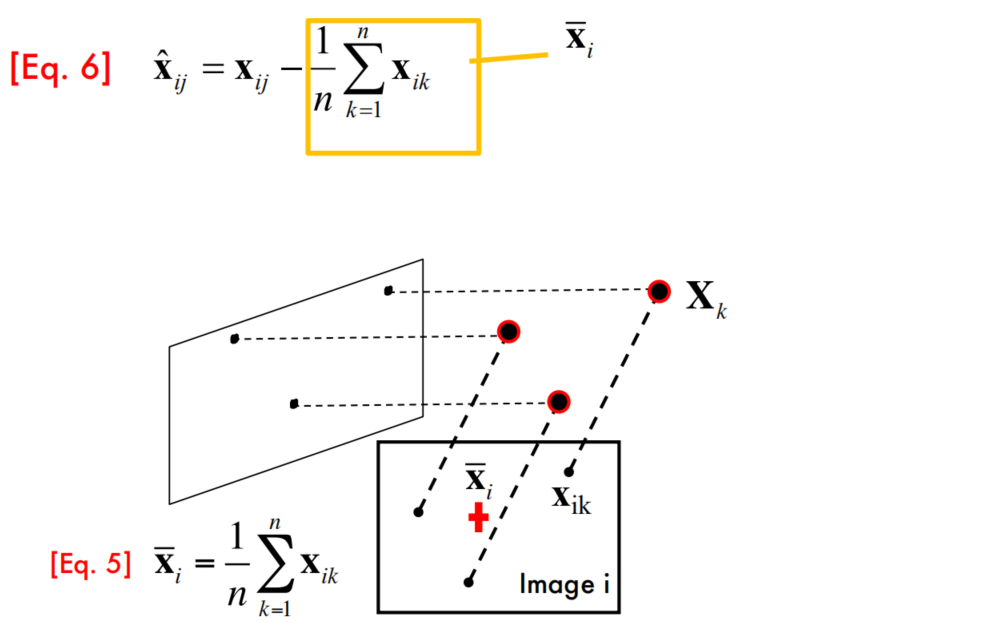
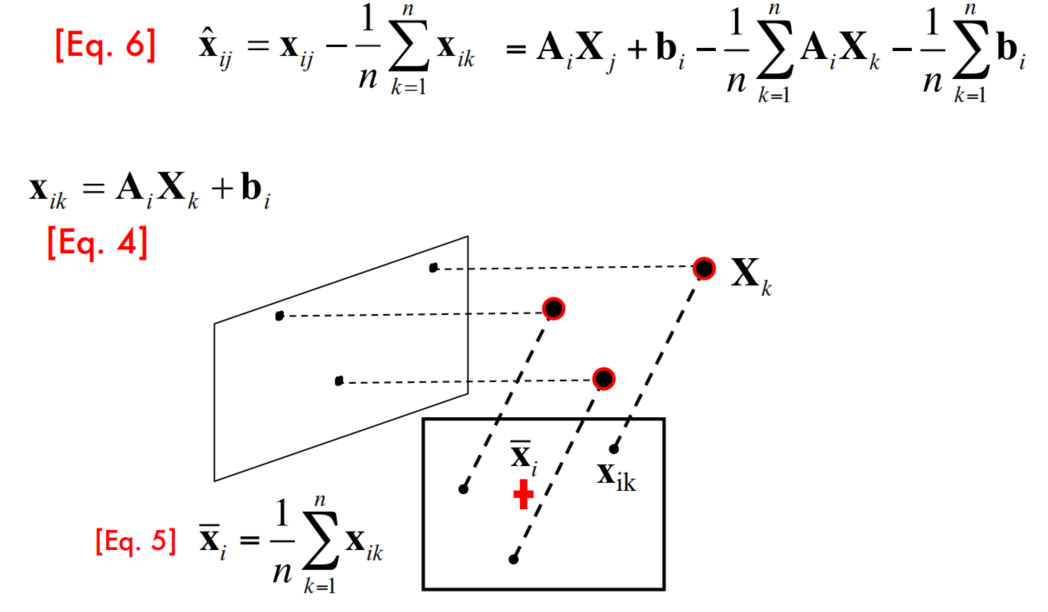
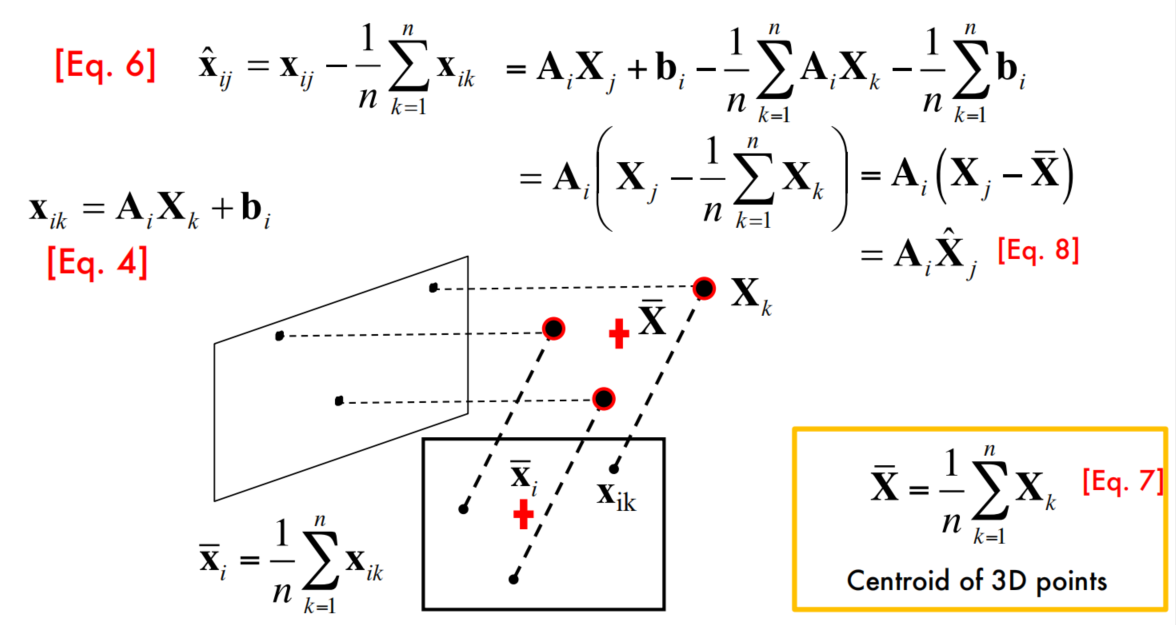
Thus, after centering, each normalized observed point is related to the 3D point by
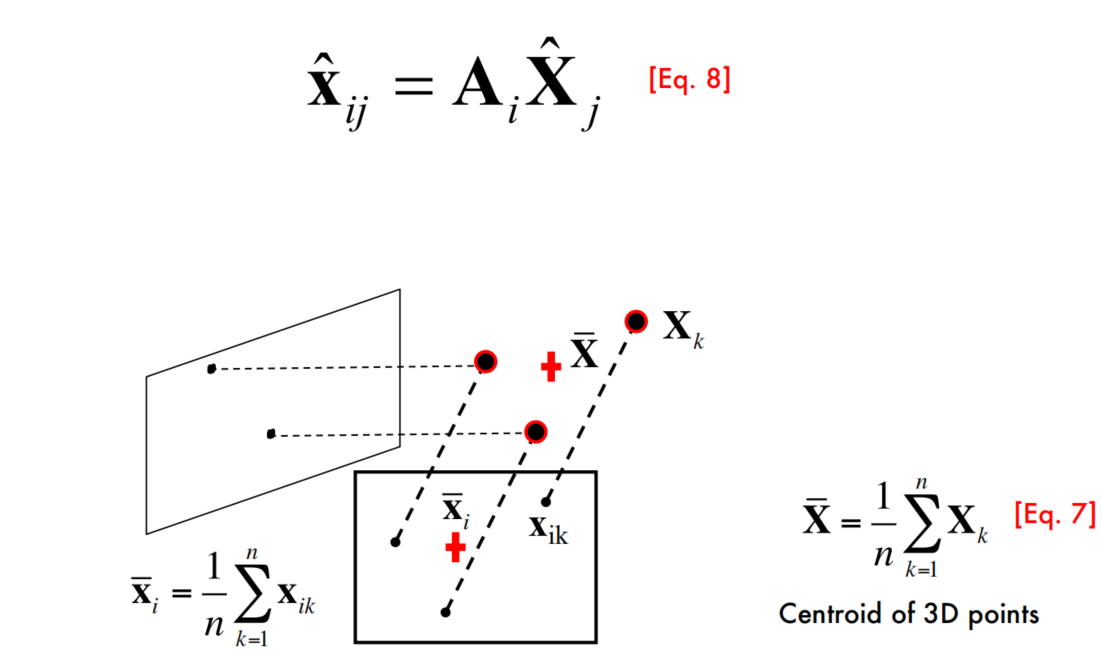
If the centroid of points in 3D = center of the world reference system
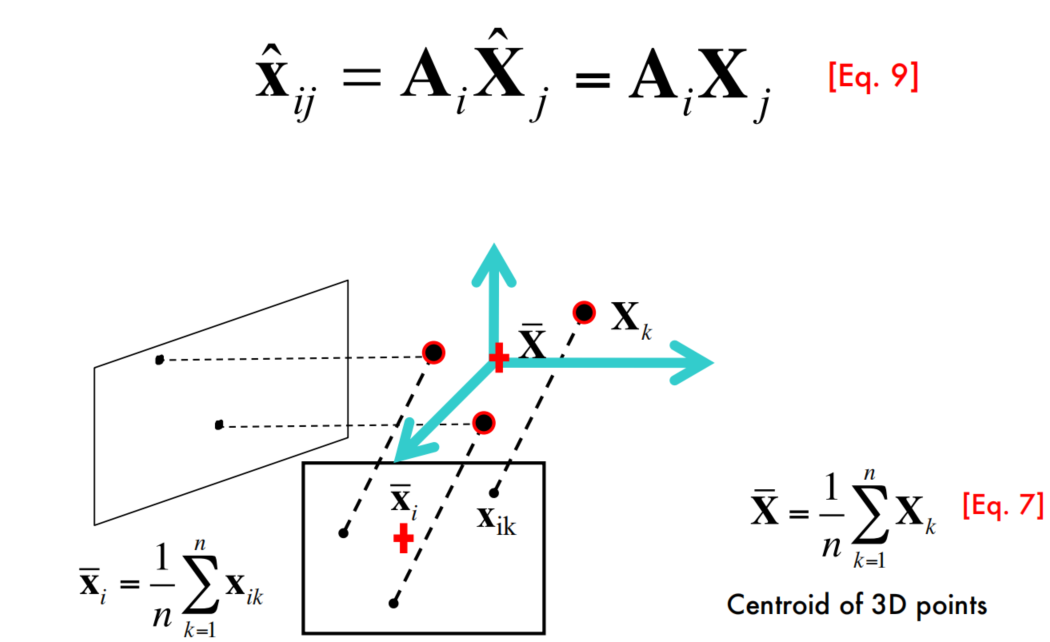
思考:
这里的几何意义应该是,本来这一组$X_j$投影到图像$i$中,还需要平移$b_i$才能够与图中的$x_{ij}$对应上;而normalize之后,平移量$b_i$就被抵消了。
Factorization
复习:线性代数
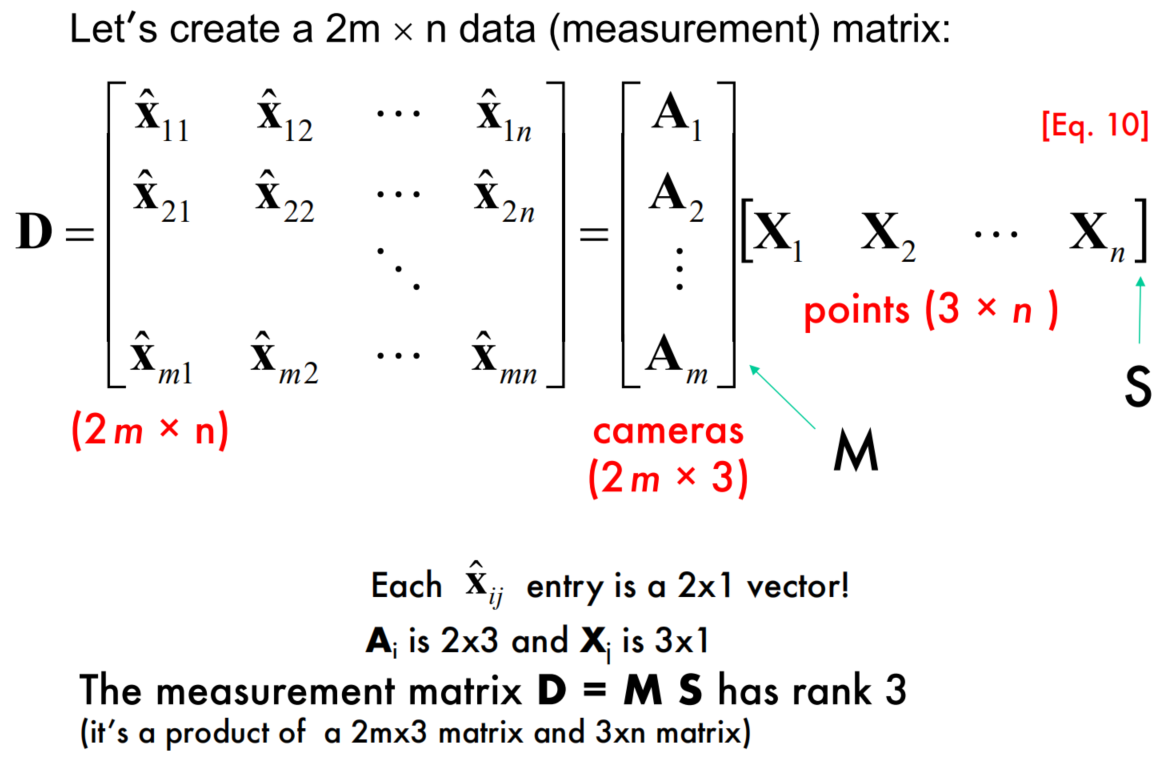
Factorizing the Measurement Matrix
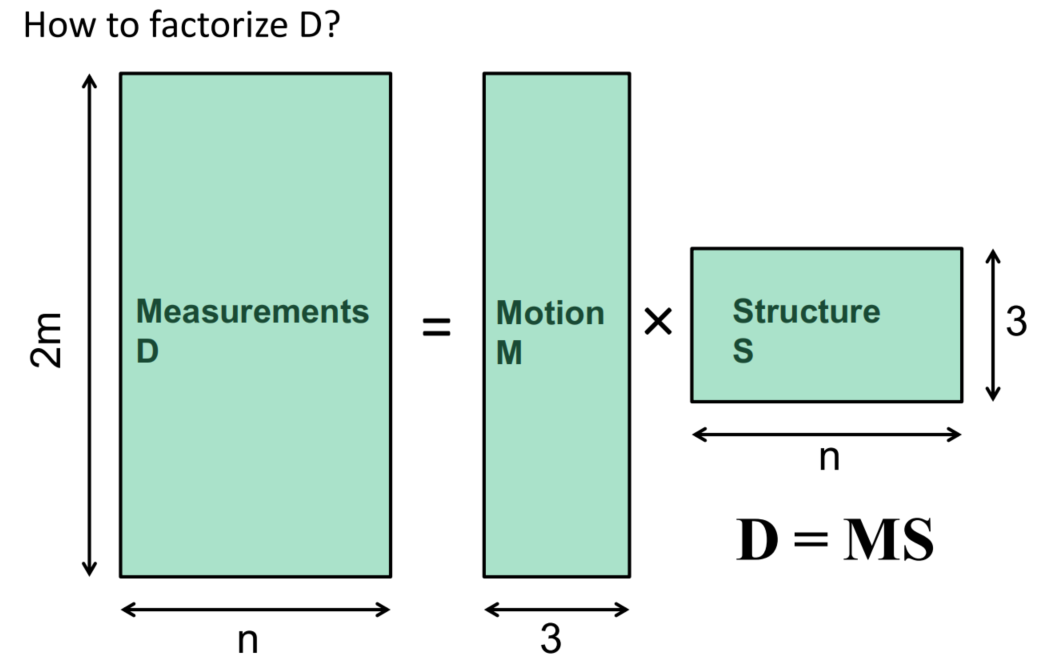
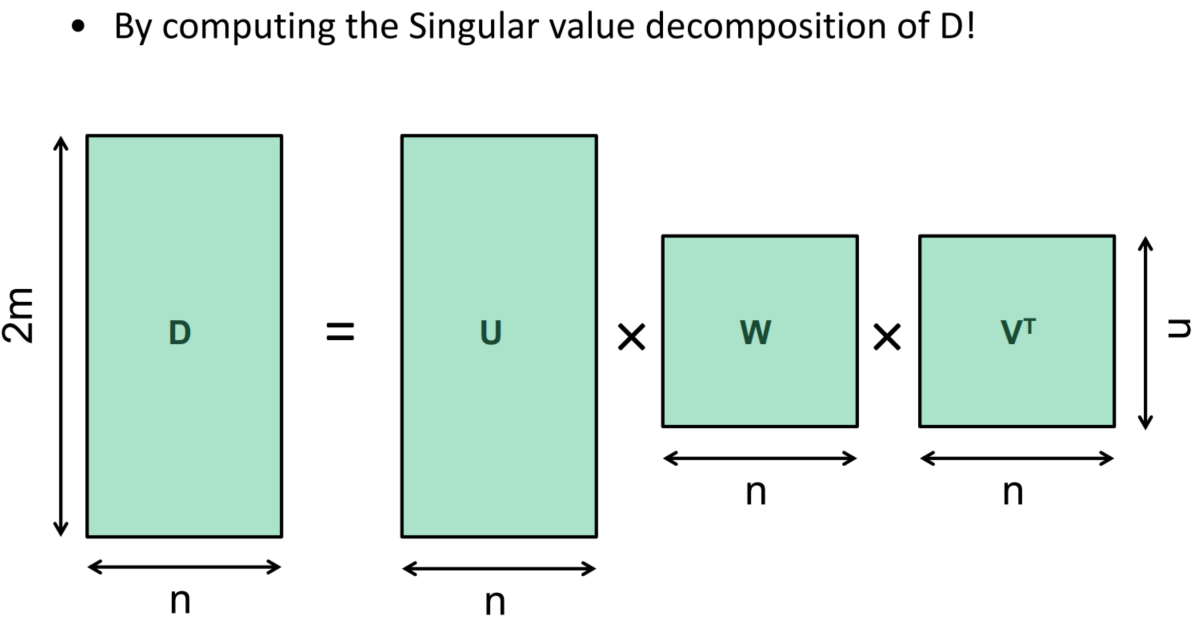
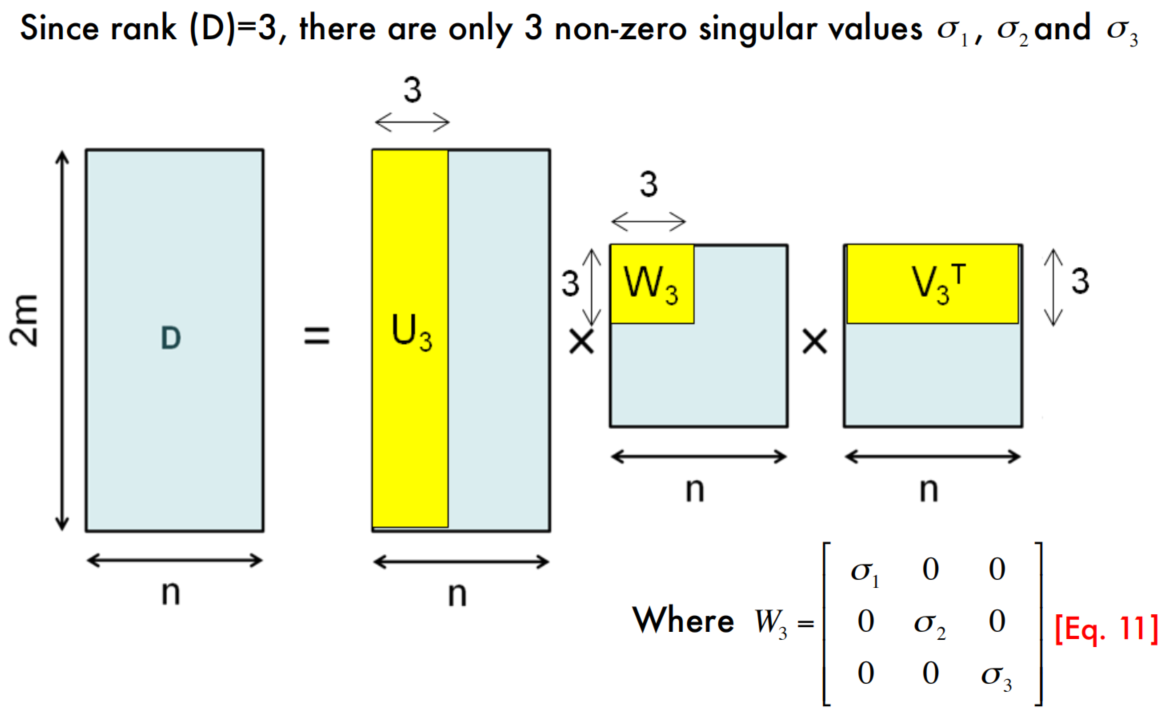
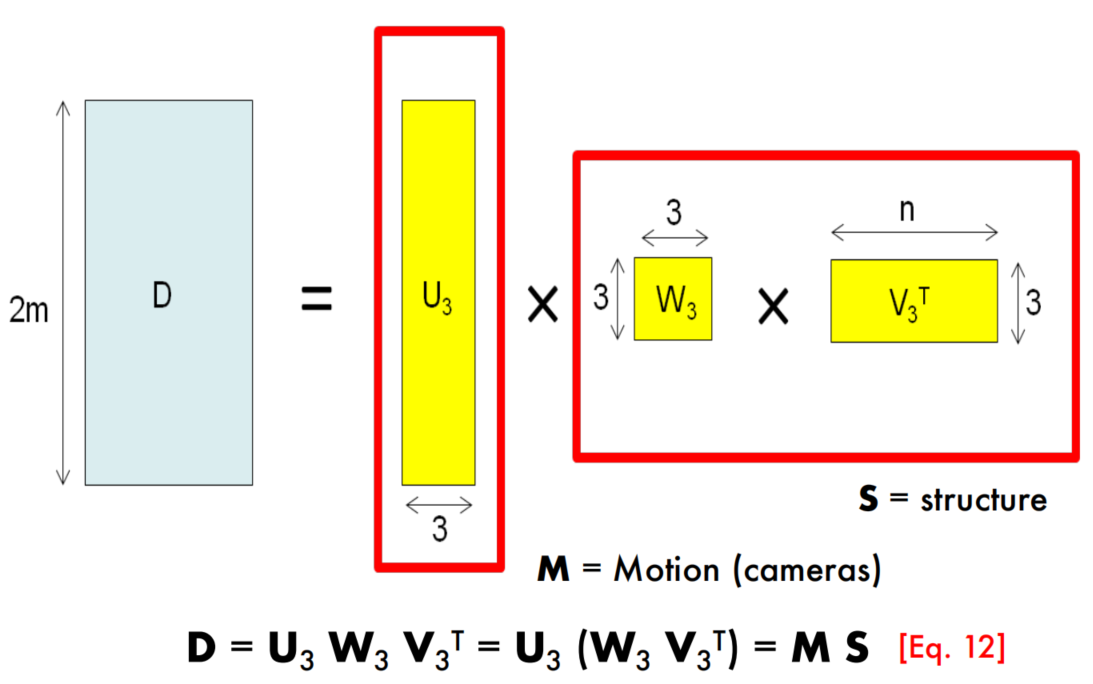

疑问
Q:什么是奇异值分解?
A:见奇异值分解-维基百科和奇异值分解(SVD)原理与在降维中的应用。
Q:这里的$W_3$指的是$W$中前3个奇异值吗?$W$中的奇异值是按照大小排序的吗?
A:从网上查到的结果是可以随意排列,奇异值与奇异向量对应上就行;不过常见的做法是将奇异值由大而小排列,如此$W$便能由$D$唯一确定了(但是$U$和$V$仍然不能确定)。这里$W$的奇异值应该是按大小排序的,$W_3$就是前3个奇异值,也是最大的3个奇异值(上面也说了$D$的秩为3,只应该存在3个非零奇异值,更小的奇异值可能就是噪声了,近似的效果也不好)。
Q:关于SVD分解的唯一性讨论
A:该部分参考网址:对SVD唯一性的理解
回顾SVD分解的定义:
对于任何一个$m \times n$的矩阵$A$,都存在这样一个分解
$$
A=U\Sigma V^T
$$
其中$U$是$m \times m$的酉矩阵,也就是$UU^* = I$;$V$是一个$n \times n$的酉矩阵;$\Sigma$是一个$m \times n$的矩阵,非对角上的元素都是0,对角线上的元素都是非负的实数,不管$A$是实数矩阵,还是酉空间中的矩阵,或者说有虚数元素。
先讨论$\Sigma$的唯一性:
假设有一个置换矩阵$J$(左乘它是做行交换,右乘它是做列交换,而且$JJ^T=I$,$J_m$表示矩阵大小为$m \times m$),那么仍然有下面的式子成立:
$$
A=(UJ_m)(J_m\Sigma J_n)(VJ_n)^T
$$
这说明,SVD分解是不唯一的。但是注意到$\Sigma$是对角矩阵,对角线上的元素(奇异值)是由矩阵$A$唯一确定的,上面的变换仅仅是将它对角线上的元素进行了一个重新的排列,我们可以固定$\Sigma$中元素的排列(比如从大到小排序),这样就可以唯一确定$\Sigma$矩阵。
再讨论$\Sigma$确定时,$U$与$V$的唯一性:
假设有一个对角方阵$K$(对角线上元素具有$e^{i\phi}$的形式,且$\phi$互不相同,$KK^*=I$,$K_m$表示矩阵大小为$m \times m$),那么仍然有下面的式子成立:
$$
A = U K_m K_m^* \Sigma K_n ( V K_n^* )^T
$$
当$K_m$对角线上第$i$个元素和$K_n$对角线上第$i$个元素相同时,有$K_m^*\Sigma K_n = \Sigma$
这说明,在$\Sigma$确定时,SVD分解得到的$U$与$V$也不是唯一的。
Affine Ambiguity
我们在上面把Affine SFM问题描述成$D=MS$,其中$D$是$2m \times n$个二维点$x_{ij}$构成的矩阵,$M$是$m$张图像的$A_i$矩阵构成的矩阵,而$S$则是$n$个三维点$X_j$构成的矩阵。
通过对矩阵$D$做SVD分解,我们可以得到$\begin{cases} &M &\approx U_3 \\ &S &\approx W_3V_3^T \end{cases}$
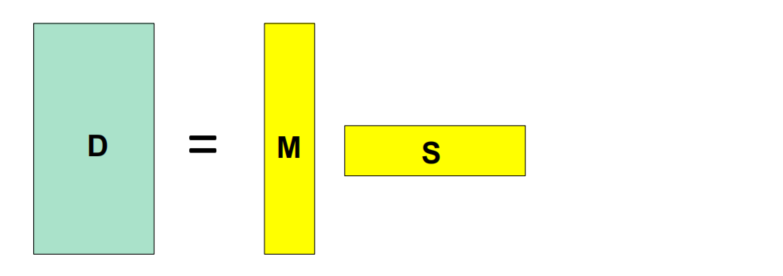
但分解的结果不是唯一的,如下所示。
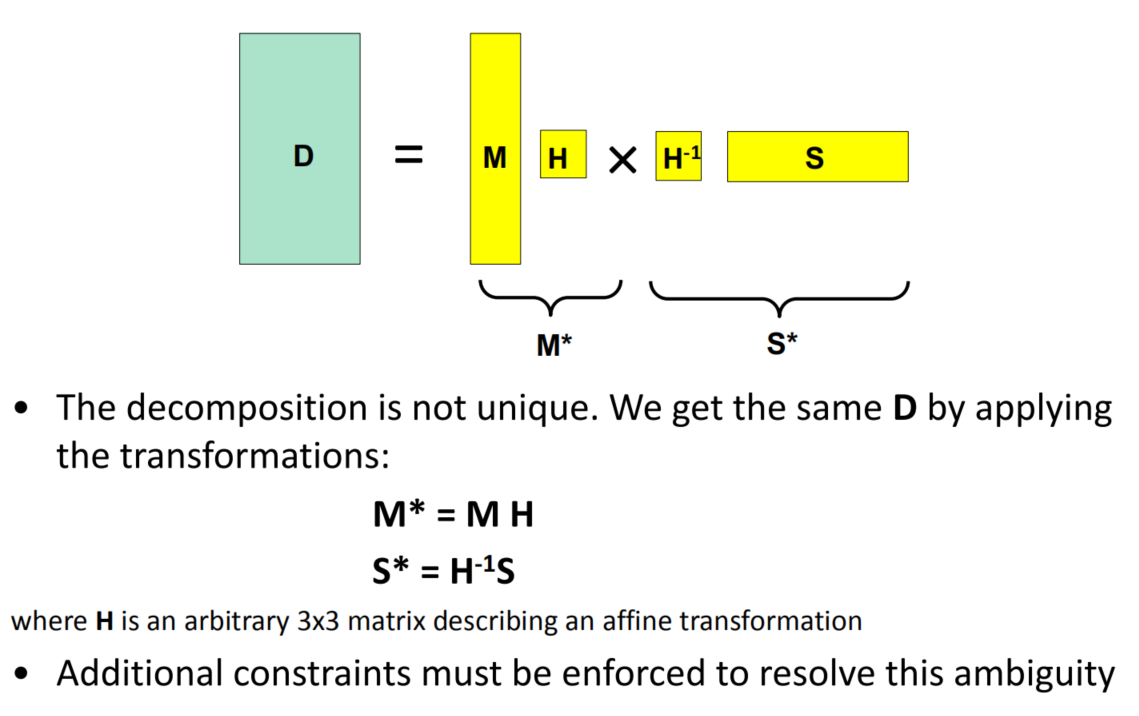
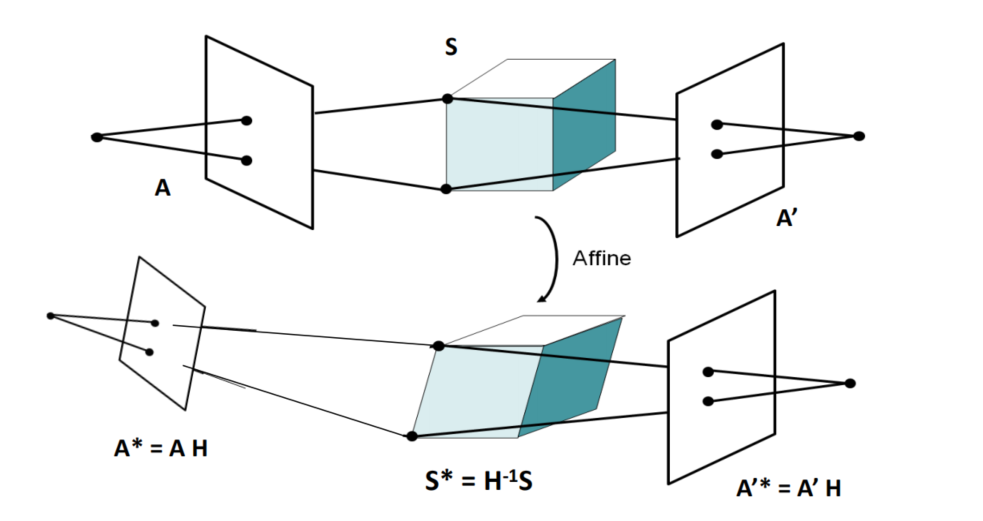
疑问
Q:这部分说的“分解的结果不唯一”指的是SVD分解结果不唯一,还是指对$M$与$S$进行一些变换可以得到同样的结果?
A:我觉得是后一种,指的是可能SVD分解的结果和实际的情况差了一个仿射变换。
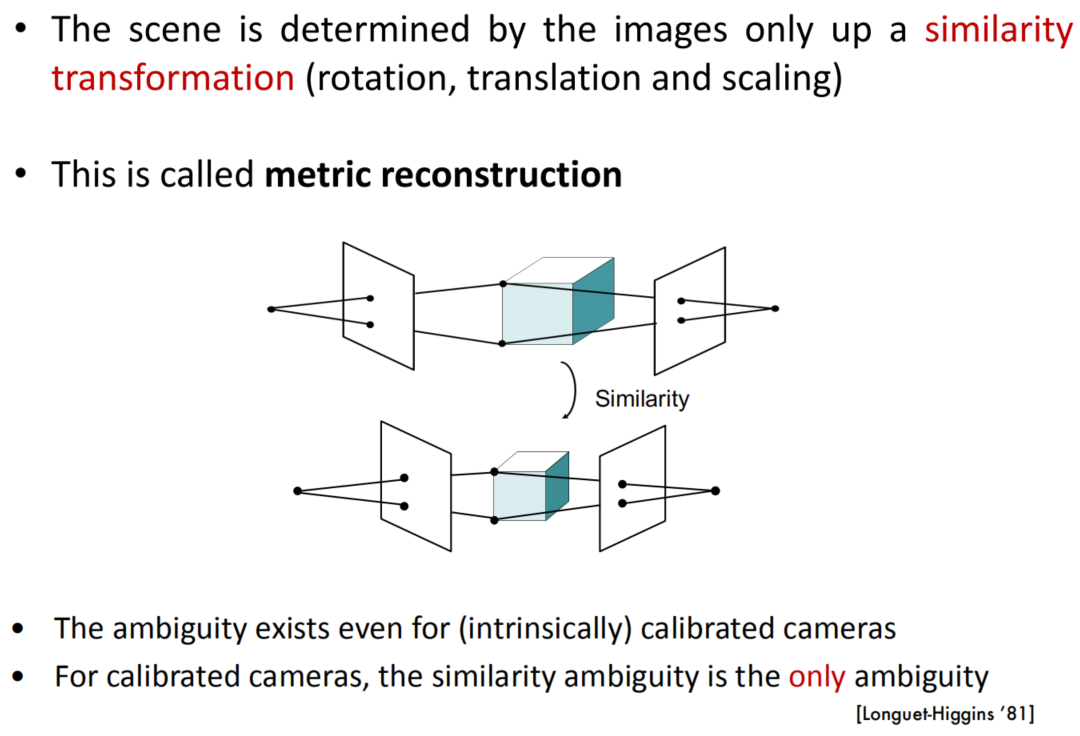
Similarity Ambiguity