slam

发布日期: 2025-05-29

文章字数: 5.4k

阅读时长: 21 分

阅读次数:

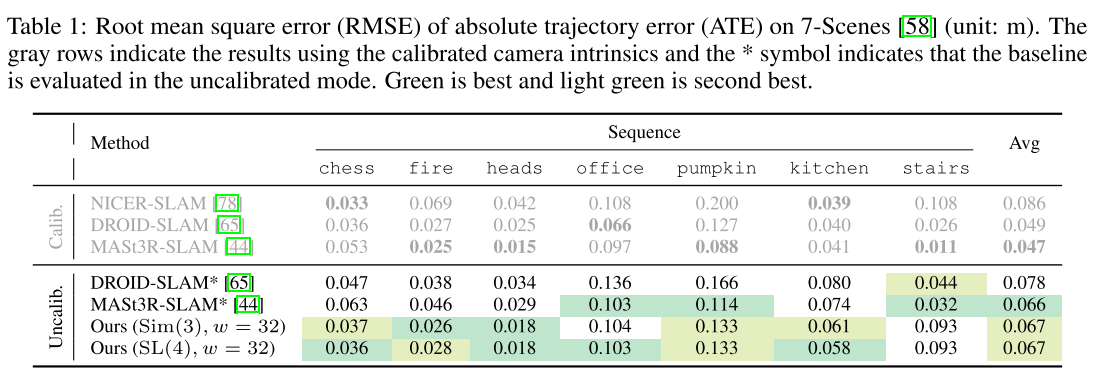
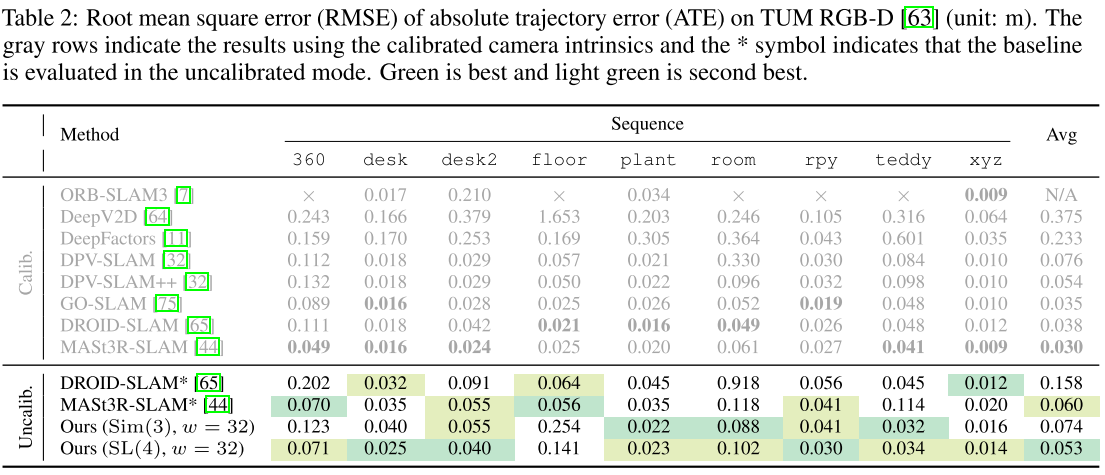
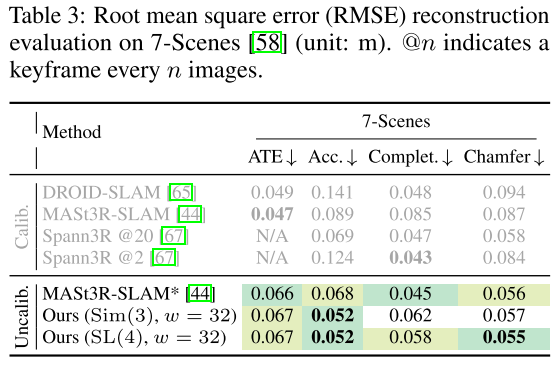
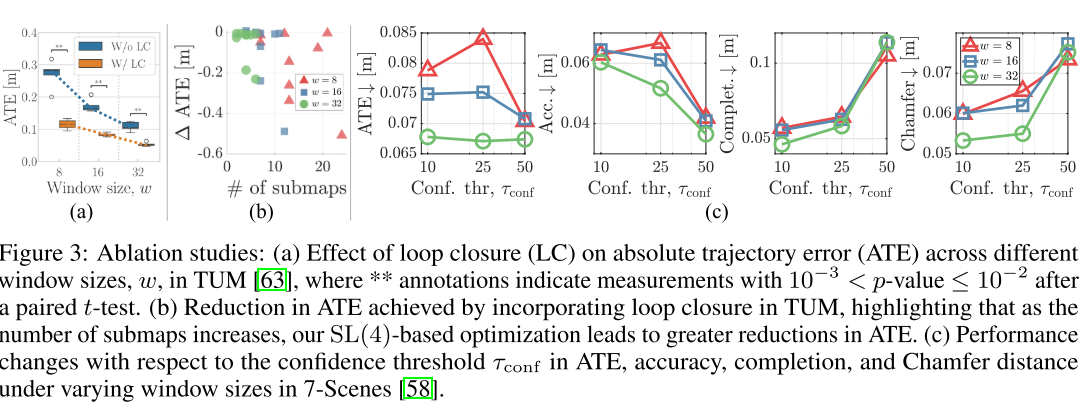
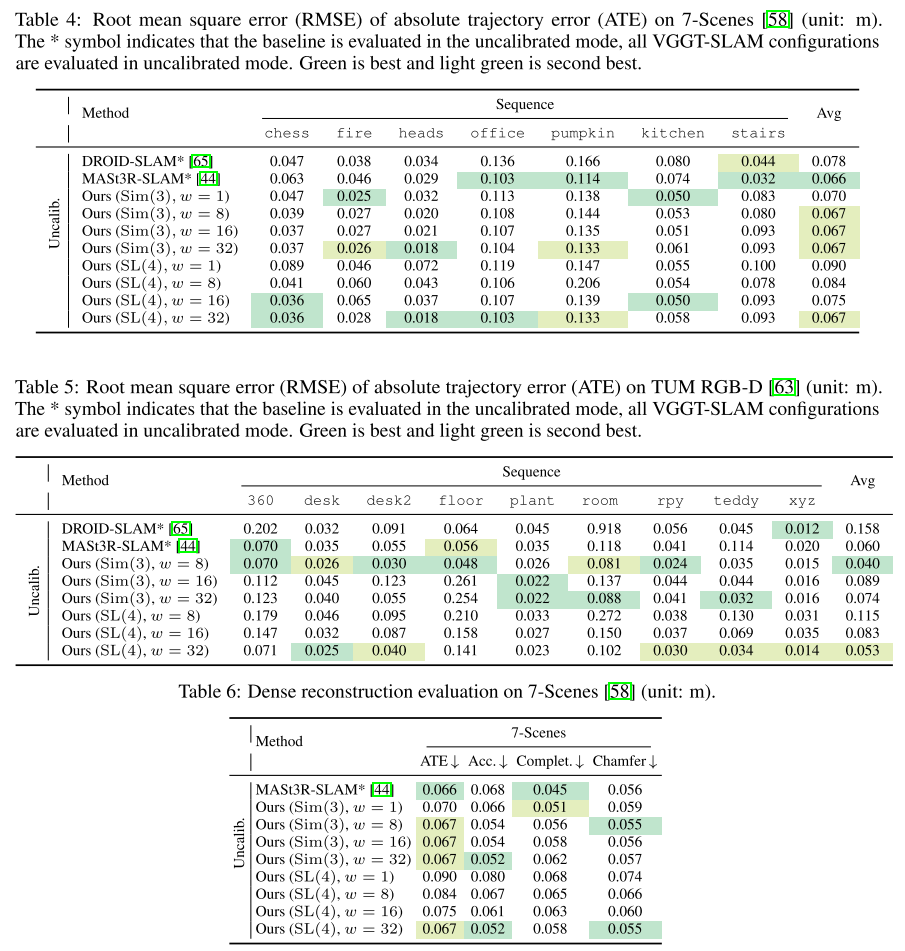
VGGT-SLAM: Dense RGB SLAM Optimized on the SL(4) Manifold

Motivation

However, VGGT is limited in the number of frames that can be processed by GPU memory. For example, in the case of an NVIDIA GeForce RTX 4090 with 24 GB, this is limited to approximately 60 frames, making larger reconstructions requiring hundreds or thousands of frames infeasible.

VGGT在GPU memory受限的情况下，做large-scale的重建是不可行的。
While related works align submaps using similarity transforms (i.e., translation, rotation, and scale), we show that such approaches are inadequate in the case of uncalibrated cameras.

相关的工作也能够对齐submap，但是在相机没有标定的情况下比较难以实现。
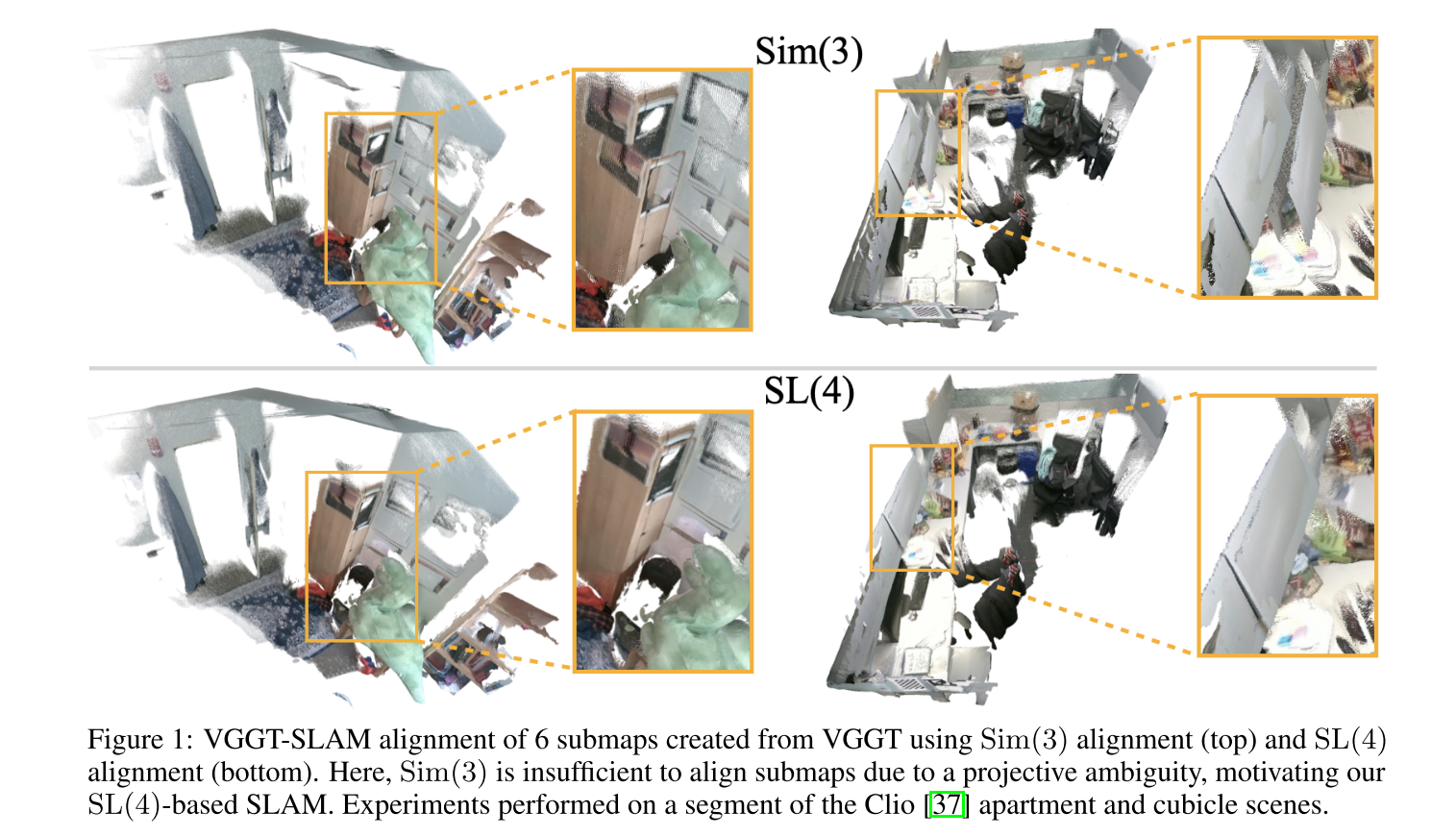
Sim(3) is insufficient to align submaps due to a projective ambiguity, motivating our SL(4)-based SLAM.

由于投影模糊，Sim(3)不足以对齐子地图，这激发了我们基于SL(4)的SLAM。

为什么sim3存在问题？

论文中的描述

One may suspect that a simple, trivial solution would be to create multiple submaps with VGGT where each submap contains at least one overlapping frame, and solve for the scale parameter between submaps (as the reconstruction does not capture metric scale), with VGGT’s estimated poses being used to align rotation and translation (i.e., estimating a Sim(3) transformation between submaps). While we demonstrate Sim(3) optimization shows impressive reconstructions in many cases, we empirically observe that the feed-forward nature of VGGT with uncalibrated cameras introduces a projective ambiguity, which in addition to the Sim(3) DOF includes shear, stretch, and perspective DOF, especially when the disparity between frames becomes small. This ambiguity cannot be fully resolved through a similarity transformation alone.

有人可能会认为，一个简单直接的解决方案是使用VGGT创建多个子地图，每个子地图至少包含一帧重叠画面，并通过求解子地图之间的尺度参数（因为重建过程无法捕获真实尺度），同时利用VGGT估计的位姿来对齐旋转和平移（即估算子地图间的Sim(3)变换）。虽然我们证明了Sim(3)优化在多数情况下能实现出色的重建效果，但实际观测发现：当使用未标定相机时，VGGT的前馈特性会引入投影歧义——这种歧义除了包含Sim(3)的自由度外，还涉及剪切、拉伸和透视自由度，尤其在帧间视差较小时更为明显。仅靠相似变换无法完全消除这种歧义。

我之前的实验

我之前也用sim3做过类似的事情，确实也是存在这个问题。虽然之后可以做BA去优化，但是BA只能优化sparse的点，毕竟track是sparse的。除非我们进行dense的track，这样我们才能真正解决这个问题，但是这样的话，开销太大了。

比如在scannet数据集上，我使用VGGT得到了下面两个submap，现在我希望进行sim3的对齐。

sim3对齐之后的位姿：

对齐之后的mesh：（分层挺明显的）

补充一个我的观点

CVPR 2025 Oral《MoGe: Unlocking Accurate Monocular Geometry Estimation for Open-Domain Images with Optimal Training Supervision》在下图指出了scale-invariant会出现不一致的监督信号，这会导致模型估计出来的depth存在歧义。

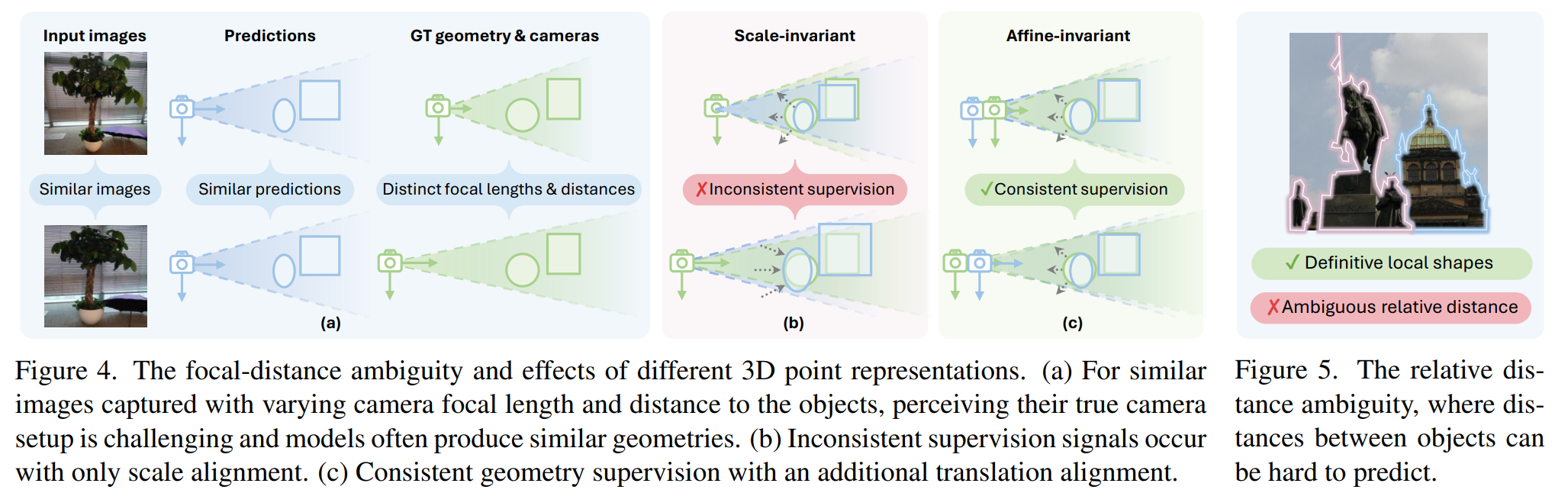
Scale-invariant就是认为gt_depth与pred_depth相差了一个scale，我们有pred_depth = scale * gt_depth；

Affine-invariant就是认为gt_depth与pred_depth相差了一个scale和shift，我们有pred_depth = scale * gt_depth + shift；

想象一下，拍摄同一个物体，距离近拍摄一张图，和距离远但是变焦缩放后再拍摄一张图像，看起来好像物体是同样大小的，但是深度却相差很大。对于背景复杂的场景，主体大小不变或者主体占比很小，而背景变化了，可能预测的depth还好，但如果背景比较简单，网络对主体的关注度更高，预测的depth就可能会出问题了。

这种情况最著名的就是，希区柯克变焦。下面是我以前拍的一段希区柯克变焦视频。

【西工大图书馆希区柯克变焦】 https://www.bilibili.com/video/BV11w7VzgESF/?share_source=copy_web&vd_source=5040c17d0665f566f786d3874bbfd13d

尽管VGGT-SLAM没有指出这一点，但是，VGGT会有这个问题吗？VGGT是用scale-invariant训练的吗？

是的是的，有的有的！看VGGT论文3.4 Training部分，depth loss和pointmap是follow的DUSt3R的。

而DUSt3R是怎么做的呢？在DUSt3R论文3.2. Traning Objective部分，这个其实就是scale-invariant的loss。

做了什么？

We present VGGT-SLAM, a dense RGB SLAM system constructed by incrementally and globally aligning submaps created from the feed-forward scene reconstruction approach VGGT using only uncalibrated monocular cameras.

关键词：Dense RGB SLAM、incrementally and globally aligning submaps、uncalibrated

论文的贡献：

Firstly, we present the first SLAM system that leverages the feed-forward scene reconstruction capabilities ofVGGT [68], extending it to large-scale scenes that cannot be reconstructed from a single inference of VGGT. Our system operates entirely with monocular RGB cameras and does not require known camera intrinsics or consistent calibration across frames. Importantly, it achieves this without any additional training.

将VGGT扩展到了large-scale的重建，只需要RGB相机，不需要相机的内参或者校准。
Secondly, while Sim(3) optimization is often sufficient, we identify and analyze scenarios where projective ambiguity arises, as presented in Fig. 1. In these cases, conventional similarity transforms do not fully resolve scale and alignment issues. We highlight this limitation and demonstrate how incorporating projective constraints addresses the problem.

虽然Sim(3)优化通常是足够的，但作者识别并分析了出现投影歧义的场景，传统的sim3不能够完全解决这个问题。而作者他们结合了projective constraints来解决这个问题。
Finally, we propose the first factor graph formulation that operates directly on the SL(4) manifold to address projective ambiguity. Even in practical scenarios, where projective ambiguity is less dominant, we show that SL(4)-based optimization achieves performance competitive with or superior to other state-of-the-art learning-based SLAM approaches, offering a principled framework for handling cases where similarity transformations are insufficient.

提出了第一个直接作用于SL(4)流形的因子图公式来解决投影歧义。即使在投影模糊不占主导地位的实际场景中，我们也表明基于SL(4)的优化实现了与其他最先进的基于学习的SLAM方法相竞争或优于的性能，为处理相似转换不足的情况提供了一个原则性框架。

与相似的工作MASt3R-SLAM的对比

Most similar to ours is MASt3R-SLAM [44]. MASt3R-SLAM leverages MASt3R to construct an impressive real time dense monocular SLAM system that does not require known calibration. Their pipeline also includes efficient optimization over Sim(3) poses and loop closures. Since MASt3R is limited to two input frames at a time, here, we desire to build on top of the more powerful VGGT architecture for a SLAM system which can leverage broader information of the scene by taking in an arbitrary number of frames for feed-forward reconstruction (bounded by computational limits) and provides direct estimates of camera poses. However, as mentioned, fusing submaps from VGGT goes beyond a traditional point cloud registration problem as alignment cannot be effectively performed with only a similarity transformation. Unlike MASt3R-SLAM, as will be discussed in Sec. 4.2, we do not need to estimate correspondences between frames.

与我们最相似的是MASt3R-SLAM[44]。MASt3R-SLAM利用MASt3R构建一个令人印象深刻的实时密集单目SLAM系统，不需要已知的校准。他们的管道还包括对Sim(3)姿势和闭环的有效优化。由于MASt3R一次限制为两个输入帧，在这里，我们希望为SLAM系统构建更强大的VGGT架构，该系统可以通过采用任意数量的帧进行前馈重建（受计算限制限制）来利用更广泛的场景信息，并提供对相机姿势的直接估计。然而，如前所述，融合来自VGGT的子地图超越了传统的点云配准问题，因为仅通过相似性变换无法有效地进行对齐。与MASt3R-SLAM不同，我们不需要估计帧之间的对应关系，这将在4.2节中讨论。

VGGT-SLAM system

输入

VGGT-SLAM接受的从VGGT来的输入是什么？下面红框的内容

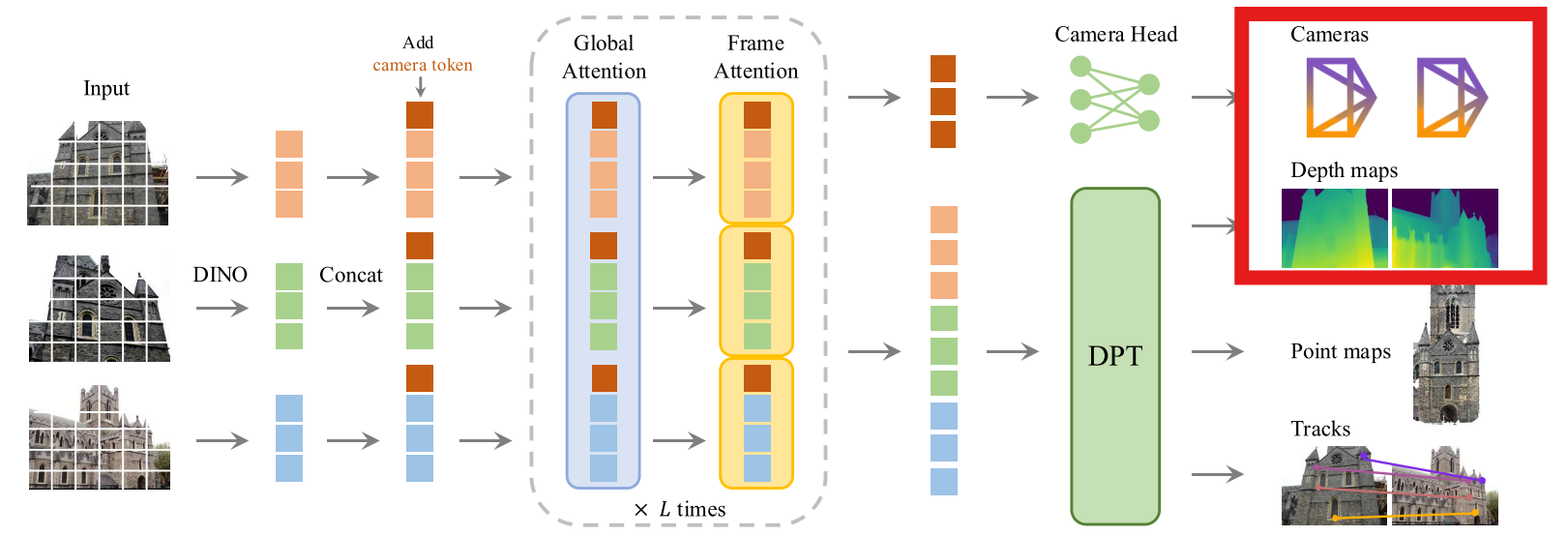
Incremental submap-based keyframe selection and generation

VGGT-SLAM是怎么选择传递给VGGT的图像集合的呢？基于图像间的视差估计，选择关键帧，传递给VGGT一个关键帧列表。

毕竟VGGT是支持视差比较大的重建的，如果喂给VGGT稠密的帧，比如1秒30帧全塞进去，效果反而不一定好。

回顾论文abstract提到的内容“实际观测发现：当使用未标定相机时，VGGT的前馈特性会引入投影歧义——这种歧义除了包含Sim(3)的自由度外，还涉及剪切、拉伸和透视自由度，尤其在帧间视差较小时更为明显”。所以这里论文选择使用关键帧列表来作为VGGT的输入。

初始化和图像集合：

首先，构建一个名为Ilatest的图像集，用于存储顺序接收到的图像。

视差估计和阈值选择：

使用Lucas-Kanade光流法（Lucas-Kanade Optical Flow）来估算相邻图像之间的视差。这种方法能够估算图像的像素位移，进而获得视差信息。
选择一个图像作为关键帧的条件是：当前图像与上一张关键帧之间的视差大于一个用户定义的阈值τdisparity。即，只有在视差足够大时，才会将当前帧选为关键帧。
视差较大的帧有助于改善相对深度估计，因为它们提供了多视角信息，这对于精确的3D重建是有益的。使用多视角信息能够减少所需处理的图像数量，提高性能。

关键帧的添加：

如果当前帧的视差足够高，它会被指定为关键帧，并添加到Ilatest列表中。
该列表的大小有限制（w），一旦达到了这个限制，新的图像就不会再加入到列表中。

构建子图像集：

除了Ilatest，每个子图（submap）还会通过追加其他两组图像来构建：
1. Mprior：从上一个子图（submap）中选取的最后一个非回环闭合的帧（即Mprior），这个帧用于维持子图之间的连续性。
2. Iloop：用于回环闭合的图像集合。最多可以包含wloop帧，这些帧将被用于子图的回环闭合。
最终，构建子图的图像集为：Ilatest ← {Mprior}∪Ilatest∪Iloop，即将上述三组图像集合拼接起来，作为子图的图像输入。

生成子图：

上述构建好的图像集将被输入到VGGT中，用于生成最终的子图Slatest。

Local submap alignment addressing projective ambiguity

为什么存在projective ambiguity呢？如何解决这个问题呢？

想要解决的问题

首先，我们跟着论文的思路，搞清楚自己要解决的问题是什么。

我们希望解决的是求一个变换矩阵H，将两个有重叠的submap对齐，这里的矩阵H可以是SE(3)，也可以是Sim(3)，同样，也可以是SL(4)。比如对于lidar slam，就是一个SE(3)矩阵，而对于单目SLAM的回环等可能存在尺度差异的情况，就是一个Sim(3)矩阵。

为什么会存在projective ambiguity？

VGGT出来的点云并不是典型的点云，而是由未标定的相机构建的点云。回顾R. I. Hartley and A. Zisserman写的《Multiple View Geometry in Computer Vision》，投影重建定理（Projective Reconstruction Theorem）指出，如果来自未校准相机的两幅图像之间的对应关系唯一地决定了基本矩阵（fundamental matrix），那么该对应关系可以用来重建相应的3D点，但只是一个15自由度的单应（homography）变换。这种变换对于任何相应的点都是相同的，除了连接相机中心的直线上的点，因为这些点不能唯一地重建。

由于相机没有标定，最终的重建结果与Ground Truth之间仅相差一个投影变换（homography），这个变换有15个自由度，属于**SL(4)**群。SL(4)是所有行列式为1的4×4实矩阵的群。论文特别强调SL(4)与常见的SL(3)有所不同，后者用于通常的图像变形任务，如图像配准和图像扭曲，它只有8个自由度。SL(4)群的投影变换可以描述三维场景的重建中出现的投影不确定性，而SL(3)则通常用于二维图像中的变换。

当场景先验可用时，重构可以转换为仿射重构（即，保留平行线），例如，如果已知点位于平行线上。如果进一步的先验已知，例如场景中的线是正交的，那么重建可以转换为度量重建（与真正的欧几里得重建只相差一个相似变换）。因此，VGGT能够利用学习到的场景先验来估计度量重建，但正如论文图1中所示，在最一般的情况下，当场景先验的估计不可靠时，重建会因projective ambiguity而不同，需要15自由度的单应性矩阵来校正。

关于Projective Reconstruction Theorem

为了更好地理解上面的问题，建议学习一下Projective Reconstruction∗

这是专门的pdf链接：https://users.cecs.anu.edu.au/~hartley/Papers/PDF/Hartley:Encyclopedia.pdf

下面是我的一个简单介绍：

关于二维平面的单应变换

从opencv文档中找一张图来举例，二维的单应变换是将一个平面内的点映射到另一个平面内的二维投影变换，描述了三维空间平面上的点，投影到不同平面上，这些平面之间的点坐标是什么关系。

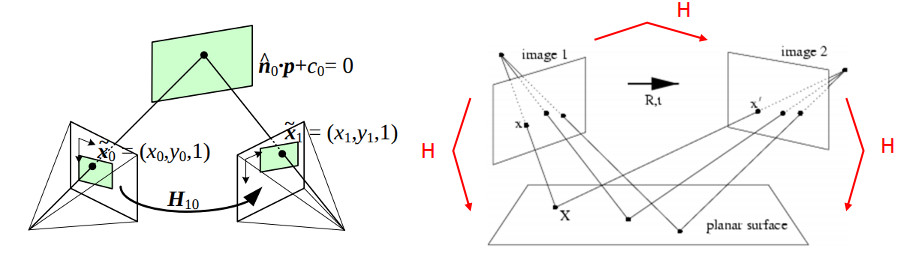
给定了三维空间的坐标系，我们可以通过匹配点求R和t，以及平面方程$n^TP+d =0$。

这样，整个过程可以描述为：
$$
\begin{align*}
s_1p_1 &= KP \\
s_2p_2 &= K(RP + t) \\
n^T P + d &= 0 \quad \Rightarrow \quad -\frac{n^T P}{d} = 1 \\
s_2p_2 &= K(RP + t \cdot 1) = K\left(RP - \frac{tn^T}{d}P\right) \\
&= K\left(R - \frac{tn^T}{d}\right)P = s_1 K\left(R - \frac{tn^T}{d}\right) K^{-1} p_1 \\
m &= \frac{s_1}{s_2} \\
p_2 &= m K\left(R - \frac{tn^T}{d}\right) K^{-1} p_1 = m H p_1 \\
H &= K\left(R - \frac{tn^T}{d}\right) K^{-1}
\end{align*}
$$
这个二维的单应变换矩阵H包含了相机内参、旋转、平移、平面方程。比如在相机标定的时候，我们拿着相机绕着标定板移动，可以通过求解H矩阵，得到相机的内参。由于p1和p2都是齐次坐标，因此H矩阵第三列最后一项h9是可以被另外两个数表示的，这导致H矩阵只有8个自由度，而且第三列与p1相乘的结果是尺度因子，后面也会被消掉。

关于三维空间的单应变换

回顾相机标定的例子，这是一个利用二维平面的单应变换求相机内参的过程，这有个前提——我们知道标定板的参数。假如我们并不知道标定板的参数，那这个过程是有歧义的，$\frac{t n^T}{d}$ 无法确定，导致 $H = K \left( R - \frac{t n^T}{d} \right) K^{-1}$ 中的 $R - \frac{t n^T}{d}$ 不唯一，从而相机内参也不唯一。这进一步导致，我们恢复出来的三维坐标具有不确定性，这种不确定性可能表现为坐标系的某种变换，例如缩放、旋转或畸变。恢复出的三维坐标可能在比例上不准确，或者点之间的相对位置关系失真，无法反映标定板在真实世界中的实际几何结构。

现在，我们抛开标定板，我们来审视三维空间中任意物体的重建，我们并不知道三维空间中物体的边长等相关的信息，也不知道相机的内参。这样的话，重建出来的点云和恢复的相机内参并不是唯一的，他们都会包含一个unknown projective transformation。

回顾课程CS231A: Computer Vision, From 3D Perception to 3D Reconstruction and beyond的透视投影矩阵(Perspective Projection Matrices)M。

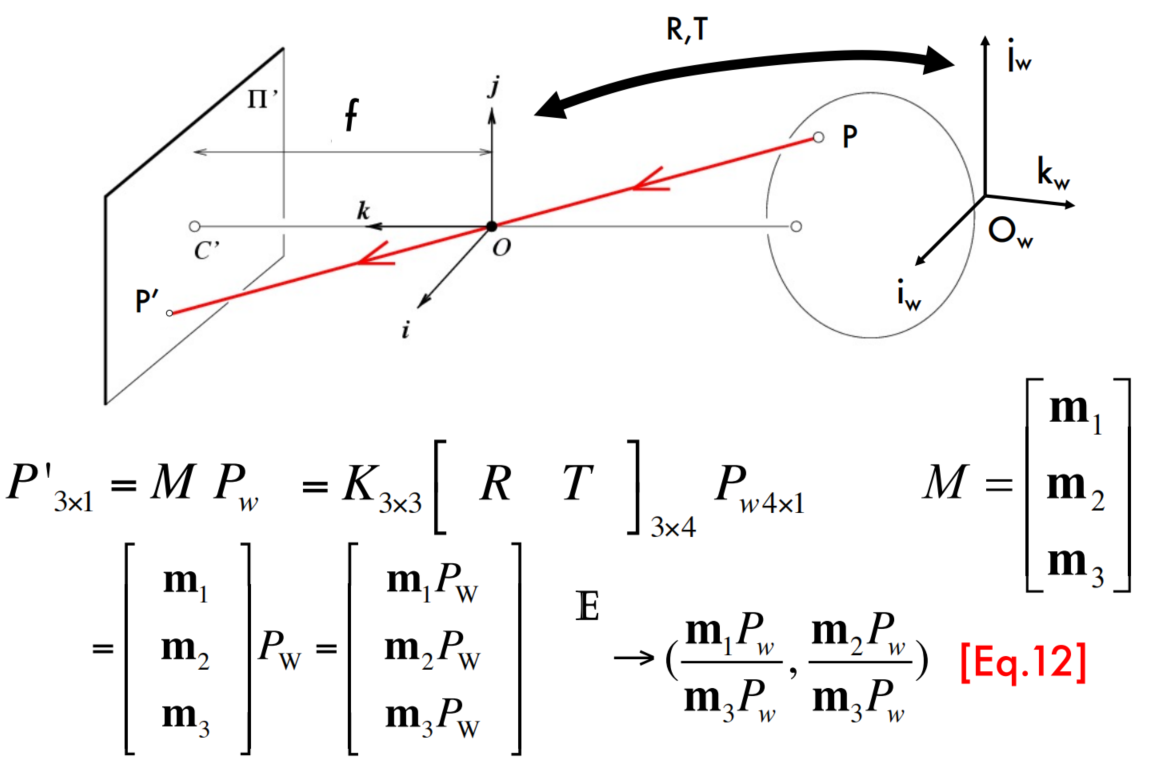
我们可以把二维平面的单应变换推广到三维空间中的单应变换：
$$
\begin{align*}
p_1 &= H_{2d} p_2 \\
p_1 &= M_1 P_1, \quad p_2 = M_2 P_2 \\
M_1 P_1 &= H_{2d} M_2 P_2 \quad \Rightarrow \quad P_1 = M_1^+ H_{2d} M_2 P_2 \\
M_1^{+} &= \left( M_1^T M_1 \right)^{-1} M_1^T \\
P_1 &= H_{3d} P_2
\end{align*}
$$
这里的H矩阵是一个非奇异的4x4矩阵，表示齐次坐标之间的映射关系。

利用这个关系很容易看出，我们并不知道三维空间中物体的边长等相关的信息，也不知道相机的内参的时候，我们只能给定对应的图像坐标xij，这样的话透视投影矩阵Pi和三维点Xj不是唯一的，他们是多解的。
$$
\begin{align*}
x_{ij} &= P_iX_j \\
&= (P_iH^{-1})(HX_j) \\
&= P_i’X_j’
\end{align*}
$$
事实上，存在一个完整的解集，表示所有可能的矩阵 H的选择。所有这些解通过投影变换相互关联，因此称为投影等价解。一个特定的解，由满足 $x_{ij} = P_iX_j$ 的相机矩阵 Pi 和点 Xj 组成，被称为场景的投影重建，它是通过给定的对应图像点计算得到的。

这里我们介绍投影重建定理（The projective reconstruction theorem）：在重建问题中，之前提到过投影等价解的问题，即通过不同的投影变换可能会得到不同的解。换句话说，从二维图像中的对应点出发，我们可能会得到多组不同的三维重建解，它们彼此通过投影变换关联。但是，如果有足够多的对应点（至少8个），并且这些点不处于某些特殊的退化配置中（例如，所有点都在同一直线上，或者在同一平面内等），那么从这些点出发得到的三维重建解是唯一的，且这些解只会在投影变换下发生变化。即，虽然通过不同的投影变换可以得到不同的解，但它们代表的是同一物理场景。

也就是说，如果我们不知道相机内参，我们三维重建出来的结果，和真实的场景会相差一个投影变换。即，存在projective ambiguity。

如何解决这个问题呢？

VGGT-SLAM输入给VGGT的图像集为：Ilatest ← {Mprior}∪Ilatest∪Iloop，这说明submap之间存在完全一样的图像帧，这样可以产生密集的匹配关系（毕竟同一张图，不需要特征匹配）。

通过这个完全一样的图像帧，就可以去求解单应矩阵。由于单应矩阵是按比例估计的，论文按行列式的四次方根进行缩放，使得行列式是单位行列式，这样得到的矩阵属于SL(4)。

对这个问题，这个工作特意设计好了，不同的submap有完全一样的图像帧，可以得到完全对应的两个点云，这么dense的correspondence，干什么不能干？所以这篇论文求一个Homography，不过维度不一样，常见的是相机标定的Homography，是平面的；而这里是三维的，从SL(3)拓展到了SL(4)。

这里重建出来的场景和gt还是会相差一个投影变换，但是论文把不同的submap与gt相差的投影变换统一起来了，这样即使分成多个submap的重建，看起来也是几何一致的，不会存在扭曲或者分层的情况。

另外，本节内容建议看对应的论文章节，更直观：

Loop closures

图像检索（步骤 1）：

计算关键帧图像描述符：在每个子图中，计算并存储每个关键帧的图像描述符，使用的是SALAD描述符。
回环闭合图像搜索：当最新的子图大小达到一定阈值（记作 w）时，系统会搜索之前子图中的关键帧，与最新子图中的关键帧进行相似性比较，寻找最相似的关键帧。
- 相似性比较是基于图像描述符的L2范数（欧几里得距离）。
- 只有当相似度超过用户定义的阈值（τdesc）时，才会考虑该帧，以避免误匹配。
- 选出一组最相似的帧（记作 Iloop），这些帧将作为当前子图的关键帧并加入子图中。

相对单应性估计（步骤 2）：

计算单应性：在图像检索过程后，系统会估计回环闭合帧（来自 Iloop）与检索到的子图之间的相对单应性（homography）。
- 该过程不需要估计特征点对应关系，而是直接使用公式（文中提到的公式(2)）在 Iloop 中的帧和其在子图中的对应帧之间计算单应性。
添加回环闭合约束：通过计算得到的单应性，为最新子图 Slatest 和检索到的子图之间提供回环闭合约束，并将这些约束添加到因子图中。

替代方法：可以不使用SALAD描述符，而是使用VGGT的微调DINO骨干网络的输出令牌来生成图像描述符。然而，这种方法需要更多的内存，因为DINO输出的特征比SALAD描述符更大。相比之下，原始的SALAD方法更为节省内存，因为它存储的是较小的描述符，并且避免了存储实际图像。