论文阅读《GaussianPro: 3D Gaussian Splatting with Progressive Propagation》

下面的笔记没有做完整，这里整理一下这篇文章的思路：（20241006）

这篇文章认为弱纹理区域，特别是平面，提供的点比较少，导致初始化不好，对此解决思路是：

• 计算3DGS的深度和法向，根据alpha-blending渲染得到深度图和法向图；

• 根据patch match算法，计算每一个pixel对应的最优平面；

  看起来是把每一块像素认为是某个平面的，深度、法向都统一了一下？

• 根据多视图几何一致性过滤不准确的深度和法向，根据过滤之后的结果与最初渲染的结果比较，重新增加一些3DGS；

• 明确了3DGS法向与渲染得到的法向之间的一致性，让平面上的3DGS更扁平。

---

Abstract & Introduction & Related Work

这篇论文看起来也是想解决3DGS目前存在的一些问题，比如sfm在弱纹理区域提供的点过少，进而导致没办法良好的初始化，比如3DGS原来的致密化策略缺少约束。论文受到classical multi-view stereo(MVS)的启发，提出了本文的方法GaussianPro，采用渐进式传播策略来指导3DGS的致密化（densification）过程。

论文在Introduction部分提到了3dgs的densification策略导致了两个限制：

1. Sensitive to Gaussian Initialization. The SfM techniques always fail to produce 3D points and leave empty in textureless regions, and therefore the densification strategy struggles to generate reliable Gaussians to cover the scene with a poor initialization.

   对高斯初始化敏感。SfM技术总是不能产生3D点，并且在无纹理的区域留下空白，因此致密化策略很难产生可靠的高斯值来覆盖初始化较差的场景。

2. Ignore the priors of the existing reconstructed geometry. The new Gaussians are either cloned to be the same as the old Gaussians or initialized with random positions and orientations. The less-constrained densification leads to difficulties in the optimization of 3D Gaussians, e.g., noisy geometries, and few Gaussians in texture-less regions, finally degrading the rendering quality. As shown in Figure 1, the results of 3DGS contain many noisy Gaussians and some regions are not covered by enough Gausians.

   忽略现有重构几何的先验。新的高斯要么被克隆为与旧的高斯相同，要么被初始化为随机的位置和方向。约束较少的密度化导致三维高斯函数的优化困难，例如几何形状有噪声，无纹理区域的高斯函数很少，最终降低了渲染质量。如图1所示，3DGS的结果包含了很多有噪声的高斯函数，有些区域没有被足够的高斯函数覆盖。

   

论文在Related Work这里提到了几点：

• 论文从MVS的深度优化中汲取灵感，改进gaussian的几何形状，从而获得更好的渲染效果；
• 3DGS对采样频率很敏感，改变相机焦距或者相机距离容易导致渲染伪影；
• 3DGS在没有明确约束场景几何结构的情况下会过度增长，导致大量冗余gaussian和内存消耗。
• 目前有一些降低3DGS存储开销的工作，但是明确约束高斯函数几何形状的工作很少，3DGS可能在远离物体表面的地方生长，从而导致冗余和新视角的渲染质量下降。论文考虑平面先验，明确约束了高斯分布的增长，可以让高斯更好的适应场景的真实几何形状，实现更好的渲染和更紧凑的表示。

基于上面几点，我觉得放在RGBD-SLAM中，光靠颜色平均值来初始化是不够的，还是需要再多考虑一下几何。毕竟我拿到了稠密的深度图，我有条件来考虑几何约束。

论文总结了自己的贡献：

• We propose a novel Gaussian propagation strategy that guides the densification to produce more compact and accurate Gaussians, particularly in low-texture regions.
• We additionally leverage a planar loss that provides a further constraint in the optimization of Gaussians.
• Our method achieves new state-of-the-art rendering performance on the Waymo and MipNeRF360 datasets. Our method also presents robustness to the varying numbers of input images.

Method

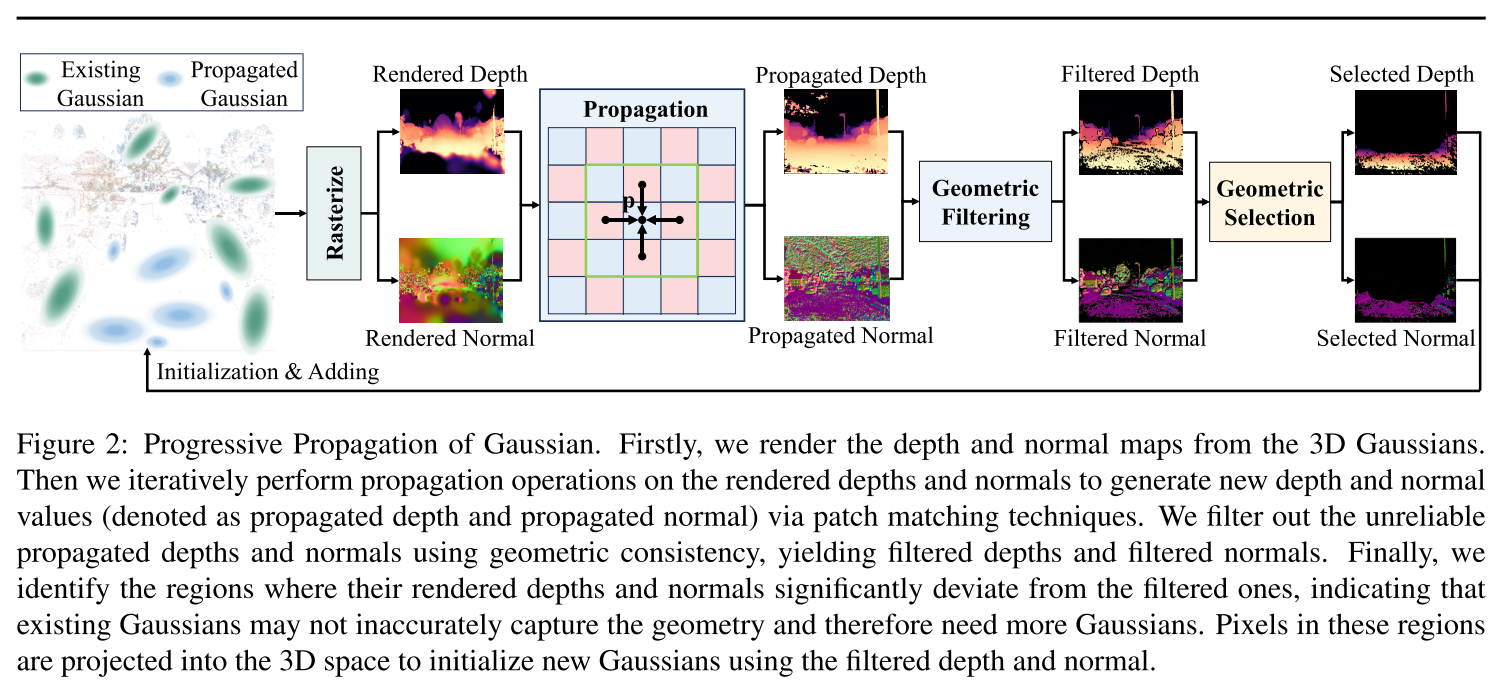
整个系统的pipeline是下面这样的：

目前的疑问，等看了后面应该就清楚了：
论文中这个段落描述的是：新深度与初始深度明显不同的像素被投影回3D空间作为3D点，这些点被进一步初始化为新的高斯点

而上面的图片描述的是：最后，我们确定了其渲染深度和法线明显偏离过滤后的区域，这表明现有的高斯函数可能不会不准确地捕获几何形状，因此需要更多的高斯函数。这些区域中的像素被投影到3D空间中，使用过滤后的深度和法线初始化新的高斯分布。

我的猜测：

• 论文认为渲染出来的深度图是不准确的，然后他们根据一些规则，从渲染的深度和法线中选择出来了准确的那些深度和法线，再和最开始渲染的初始深度进行比较，有明显差异的就初始化为新的高斯点。

  一种逻辑自洽的感觉，论文似乎想让高斯渲染出“合理的”深度图和法线图。

  不过，如果已经有深度图的话，论文这样的思路应该怎么实现呢？？？

Hybrid Geometric Representation

论文提到一个问题：Due to the discrete and irregular topology of the 3D Gaussians, it is inconvenient to perceive the connectivity of geometries, like searching neighboring Gaussians on a local surface. As a result, it’s difficult to perceive the existing geometry to guide the Gaussian densification.

针对这个问题，论文给出了解决方案：Hybrid Geometric Representation，即将3D Gaussian投影到结构化的二维图像空间（深度和法线）。