ICP算法详解
原论文浅析&补充:A Method for Registration of 3-D Shapes
ICP算法最早于1992年由论文《A Method for Registration of 3-D Shapes》提出,论文提到ICP算法可以用于以下的几种情况:
- 点集
- 线段集(折线)
- 隐式曲线(用数学公式表示曲线)
- 参数曲线(用参数映射表示曲线)
- 三角面片(应该就是现在的mesh)
- 隐式表面(用数学公式表示的表面)
- 参数表面(用参数映射表示的表面)

关于3、4、6、7点有疑惑的,可以看几何的隐式表示与显示表示,或者看GAMES101: 现代计算机图形学入门第5周、第6周的课件。
由于我们主要关注点集之间的配准,因此下面主要讲论文的IV. THE ITERATIVE CLOSEST POINT ALGORITHM部分,其他部分可以看原论文。
ICP算法的定义
从下面可以看出,ICP算法最核心的问题就两个,一个是如何计算最近点(最近邻问题),一个是如何求解旋转和平移(非线性最小二乘问题)。

对于有$N_p$个点${p_i}$的点集$P$,和有$N_x$个点、线段或三角面片的目标形状$X$,ICP算法可以定义为:
$P_k$表示第$k$次迭代更新之后的点集,$q_k$表示第$k$次迭代中计算得到的旋转和平移,其中$P_0=P$,$q_0=[1,0,0,0,0,0,0]^t$,$q_0[0:3]$是单位四元数,表示旋转,$q_0[4:6]$是平移向量,表示平移。
算法的流程为:
计算本次迭代的最近点集,$Y_k = C(P_k,X)$,平均复杂度是$O(N_p logN_x)$,最坏的情况下复杂度是$O(N_pN_x)$。需要注意,$Y_k$是目标形状$X$上的点。
计算最近点集的问题也叫做最近邻问题,后面会详细展开讲。这里ICP认为距离最近的点就是对应点,根据对应点能计算旋转和平移。
这部分和快速排序的时间复杂度一样
计算本次迭代的旋转和平移,$(q_k,d_k)=Q(P_0,Y_k)$,时间复杂度是$O(N_p)$
这部分在论文III. MATHEMATICAL PRELIMINARIES部分有介绍,下面也会详细展开
应用本次计算的旋转和平移,更新点集,$P_{k+1} = q_k(P_0)$,时间复杂度是$O(N_p)$
当均方误差的变化低于预设的阈值时,终止迭代。这个阈值指定了配准过程的期望精确度。
ICP核心问题一:最近邻问题
这里给一个高翔新书《自动驾驶与机器人中的SLAM技术-从理论到实践》中的部分介绍。


ICP核心问题二:非线性最小二乘问题
原论文方法一
对应论文中III. MATHEMATICAL PRELIMINARIES部分的C. Corresponding Point Set Registration
对应上述方法的第二步,即“计算本次迭代的旋转和平移,$(q_k,d_k)=Q(P_0,Y_k)$,时间复杂度是$O(N_p)$”。
下面的方法应该就是SVD分解的方法。
下面是论文中提到的求解方法,比较类似SVD分解。


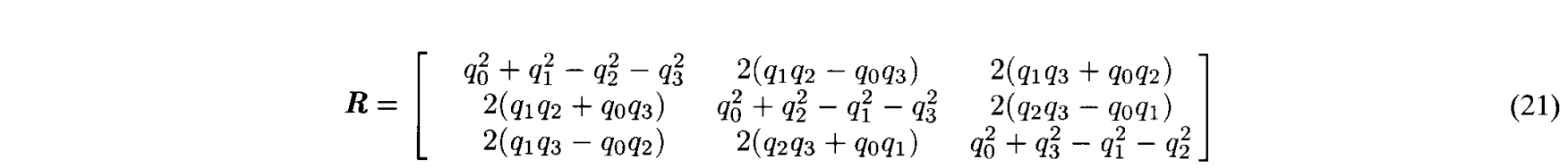
原论文方法二
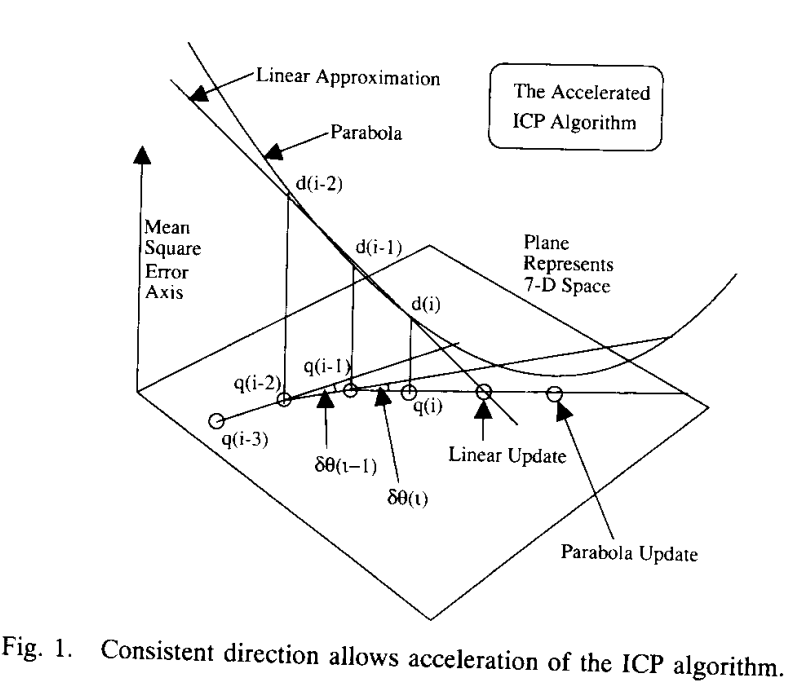
对应论文中IV. THE ITERATIVE CLOSEST POINT ALGORITHM部分的C. An Accelerated ICP Algorithm
对应上述方法的第二步,但是替换掉了旋转和平移的求解方法。
下面的方法应该是梯度下降法。
下面是原论文中提到的方法,比较类似梯度下降法,和求解最小二乘问题



常用方法一:SVD分解



常用方法二:梯度下降法

经典ICP算法框架
在高翔新书《自动驾驶与机器人中的SLAM技术-从理论到实践》中,对3D点对点ICP算法的描述如下所示。


G-ICP论文中给出了标准ICP算法框架,如下所示。

拓展:Gaussian Splatting中的最近邻问题
在gaussian splatting中,包括了submodules/simple-knn,这个simple-knn并不是聚类算法,而是一个K近邻算法。
代码对应部分
Gaussian Splatting中使用K近邻算法的目的是为了实现初始化,每个初始化高斯点的尺度是其到最近的k个点的平均距离。

simple-knn代码实现
Gaussian Splatting中直接调用的函数如下:
// 定义一个函数 distCUDA2,参数是一个常量引用 torch::Tensor 类型的 points,返回值类型是 torch::Tensor
torch::Tensor
distCUDA2(const torch::Tensor& points)
{
// 获取 points 张量的第一个维度的大小,即点的数量 P
const int P = points.size(0);
// 创建一个选项对象 float_opts,类型与 points 的数据类型相同,但数据类型设置为 torch::kFloat32
auto float_opts = points.options().dtype(torch::kFloat32);
// 使用 float_opts 选项创建一个大小为 P 的张量 means,初始值为 0.0,数据类型为 float32
torch::Tensor means = torch::full({P}, 0.0, float_opts);
// 调用 SimpleKNN::knn 函数,传入 P(点的数量)、points 的连续内存数据(转换为 float3 指针)、means 的连续内存数据
// 代码中默认的K=3,这里means得到的就是每个点到最近的三个点的平均距离的平方
SimpleKNN::knn(P, (float3*)points.contiguous().data<float>(), means.contiguous().data<float>());
// 返回 means 张量
return means;
}
其中,SimpleKNN::knn是一个“基于 Morton 编码的 K 近邻(KNN)查找算法”,这里用GPT根据submodules/simple-knn的代码生成了如下伪代码,方便理解:
// Step 1: Normalize points and compute Morton codes
// 计算xyz坐标的最小值和最大值,并且进行归一化&计算morton编码
minn = min(points)
maxx = max(points)
for each point in points:
morton_code = compute_morton_code(point, minn, maxx)
// Step 2: Sort Morton codes and indices
// 对morton编码进行排序和索引
sort(morton_codes, indices)
// Step 3: Divide points into blocks and compute bounding boxes
// 分块,并且计算每个块的最小值最大值
blocks = divide_into_blocks(points, block_size)
for each block in blocks:
compute_min_max(block)
// Step 4: KNN search
// K近邻搜索
for each point in points:
// 首先从该点所属的block中找最近点
nearest_neighbors = find_nearest_neighbors_in_block(point, block)
for each block in blocks:
// 之后再从其他的block中找最近点并且进行更新
if distance_to_block(point, block) < furthest_distance(nearest_neighbors):
update_nearest_neighbors(point, block, nearest_neighbors)
// 计算与最近K个点的平均距离的平方
mean_distance = compute_mean_distance(nearest_neighbors)Morton编码
Morton 编码(Morton Code),也称为 Z-order 曲线(Z-order Curve),是一种将多维数据映射到一维的空间填充曲线。在这种映射中,具有相邻多维坐标的点在映射到一维后也保持相邻的概率较高。
Morton 编码的原理
Morton 编码通过交替取每个维度的比特位来实现。例如,对于三维坐标 (x, y, z),它将每个坐标的二进制表示交替组合,形成一个新的整数。具体步骤如下:
- 将每个坐标归一化到 [0, 1] 范围内: 这通过将坐标减去最小值并除以最大值减去最小值来实现。这样可以确保所有坐标都在相同的范围内,有助于后续的比特操作。
- 将归一化后的坐标映射到一个固定范围内的整数: 例如,将归一化后的 [0, 1] 范围内的坐标映射到 [0, 1023] 范围内(即 10 位二进制数)。
- 将每个维度的比特交替合并: 将每个坐标的二进制表示交替取出,并组合成一个新的整数。这个过程叫做“bit interleaving”。




