论文阅读《Compact 3D Gaussian Splatting For Dense Visual SLAM》
Motivation
论文提到最近的3DGS SLAM都是建立在大量冗余3D高斯椭球上的,导致了高内存占用和存储成本,以及很慢的训练速度。
为了解决这个问题,他们提出了一种紧凑的3D高斯飞溅SLAM系统,该系统减少了高斯椭球的数量和参数大小。
Contributions
- 我们提出了一种新的基于GS的SLAM系统,该系统具有紧凑的高斯场景表示,实现了快速的训练和渲染速度、准确的姿态估计,并显著提高了存储效率。
- 提出了一种新的基于滑动窗口的在线掩蔽方法,以消除冗余高斯椭球的数量,同时在训练过程中实现高保真度。
- 我们观察并分析了三维高斯椭球的几何相似性,并提出了一种基于码本的方法来有效地恢复SLAM系统运行过程中每个高斯点的几何。针对摄像机跟踪性能相对较低的问题,提出了一种基于关键帧的全局BA方法,该方法具有重投影损失。
- 我们在不同的数据集上进行了全面的实验,渲染速度提高了近176%,内存使用压缩率超过1.97倍。
System Pipeline
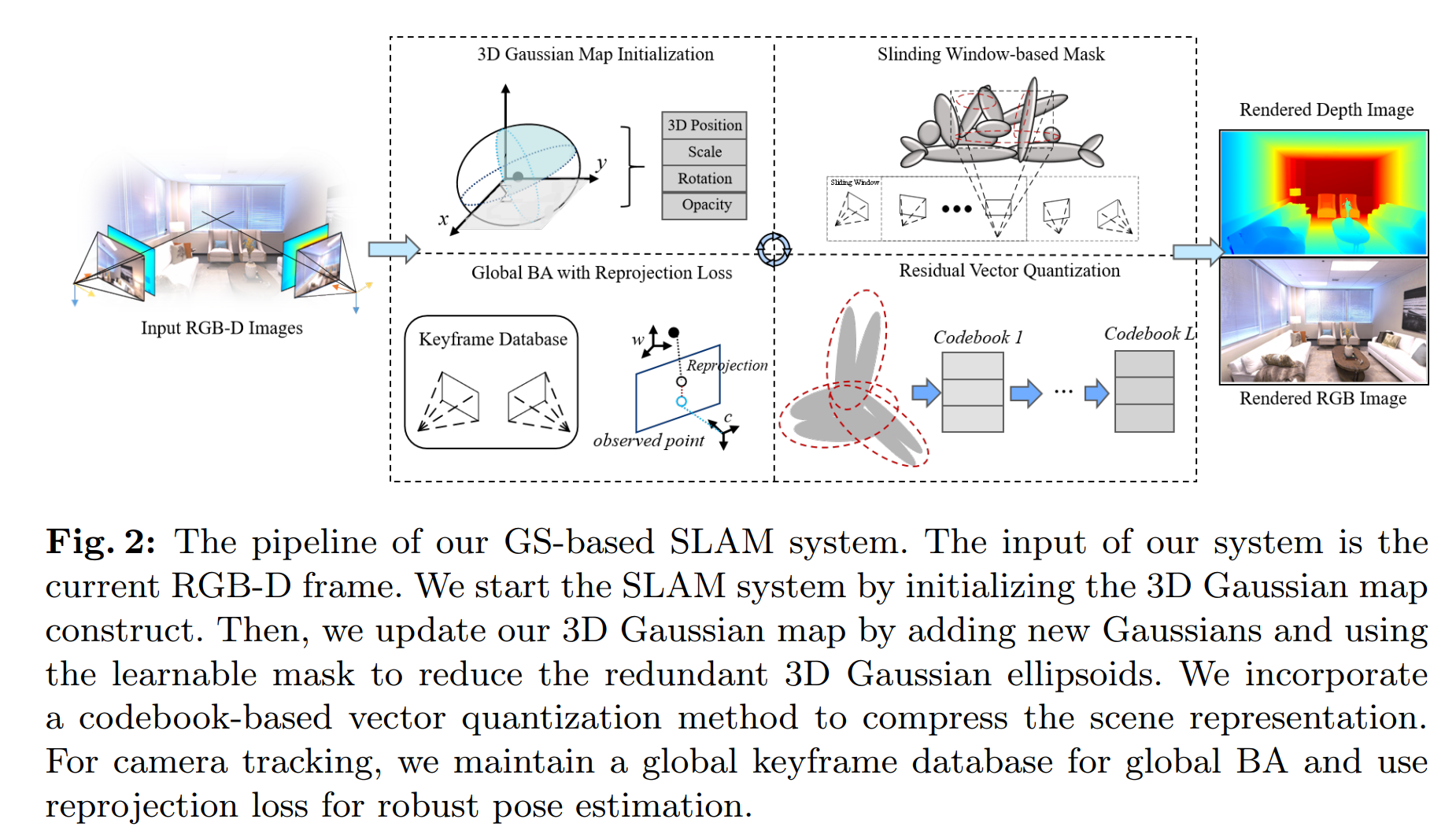
乍一看,有点像是SplaTAM的图呢,会不会是在SplaTAM的基础上改进来的?
讨论分析
看了一下论文写的一些内容,我都不是很理解:
3.2 Sliding Window-based Mask部分
3.2 Sliding Window-based Mask部分stop gradient operator sg(·)输出的结果是什么?
根据下面的信息解释这个公式:
We introduce a learnable mask parameter $m \in R^N$ and a corresponding binary mask $M \in {0, 1}^N$, N is the number of Gaussian ellipsoids.
$$
M_n = sg (\mathbb{I}[Sig(m_n) > \epsilon] - Sig(m_n)) + Sig(m_n)
$$
where $n$ is the index of the Gaussian ellipsoids, $\epsilon$ denotes the mask threshold. Inspired by [1], we employ the stop gradient operator $sg(·) $to calculate gradients from binary masks. $\mathbb{I}$ and $Sig(·)$ denote the indicator and sigmoid function. This formulation of mask strategy allows us to effectively combine the influence of volume and opacity of Gaussian ellipsoids.根据GPT的解释,结论:
sg()就是停止梯度计算,相当于with_no_grad()。
这里就是计算一个1-sig+sig=1,或者计算一个0-sig+sig=0
因为这里不连续所以不计算梯度。
3.2 Sliding Window-based Mask部分为什么使用这样的损失函数?
追问:为什么使用如下的损失函数
We formulate the loss function $L_m$ of our mask:
$$
L_m = \frac{1}{N} \sum_{n=1}^{N}Sig(m_n)
$$
这个损失函数真的非常奇怪,确定不是1-Sig吗?这个目的是让所有的mask都变成0啊???
3.3 Geometry Codebook
3.3 Geometry Codebook这部分的公式也不是太看得懂,没理解codebook的作用,这里也没有详细介绍。
后续看《Compact 3D Gaussian Representation for Radiance Field》,看明白了。。。
评价:
这篇论文主要是压缩3DGS的大小,做了两方面的工作,一个是基于可学习的mask和视锥体来过滤高斯,一个是通过codebook压缩相似的高斯。
其他方面倒是没感觉特别突出,对于Global BA部分,它说维护的关键帧数量比其他GS SLAM大得多,个人觉得这不是优点。比如RGBD GS-ICP SLAM就提到了,关键帧数量越多越容易导致误差累积的问题。



