CS231A Lecture 7:Multi-view geometry (2)
Reading:
[HZ] Chapter 10 “3D reconstruction of cameras and structure”
[HZ] Chapter 18 “N-view computational methods”
[HZ] Chapter 19 “Auto-calibration”
[FP] Chapter 13 “projective structure from motion”
[Szelisky] Chapter 7 “Structure from motion”
Perspective SFM
Structure from motion problem
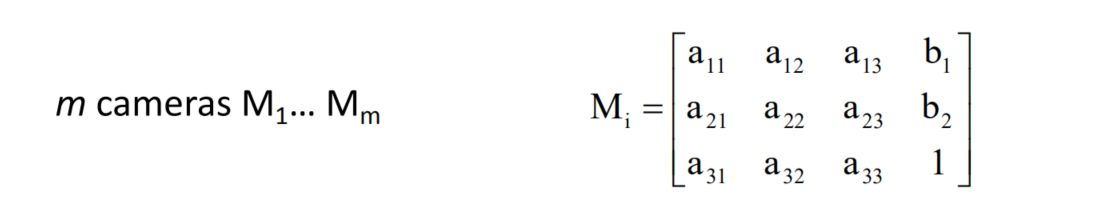
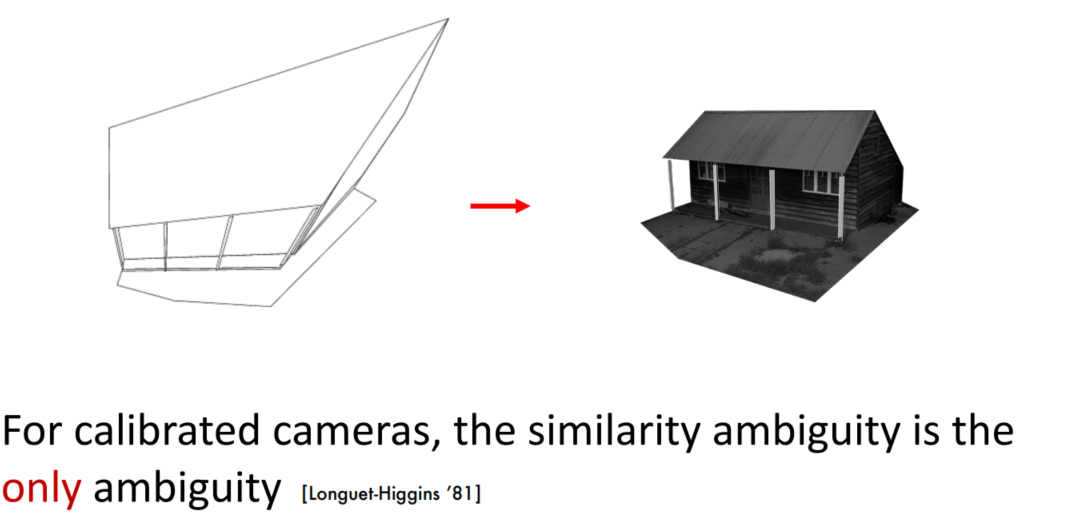
Structure from Motion Ambiguities
ambiguities for 3D reconstruction:

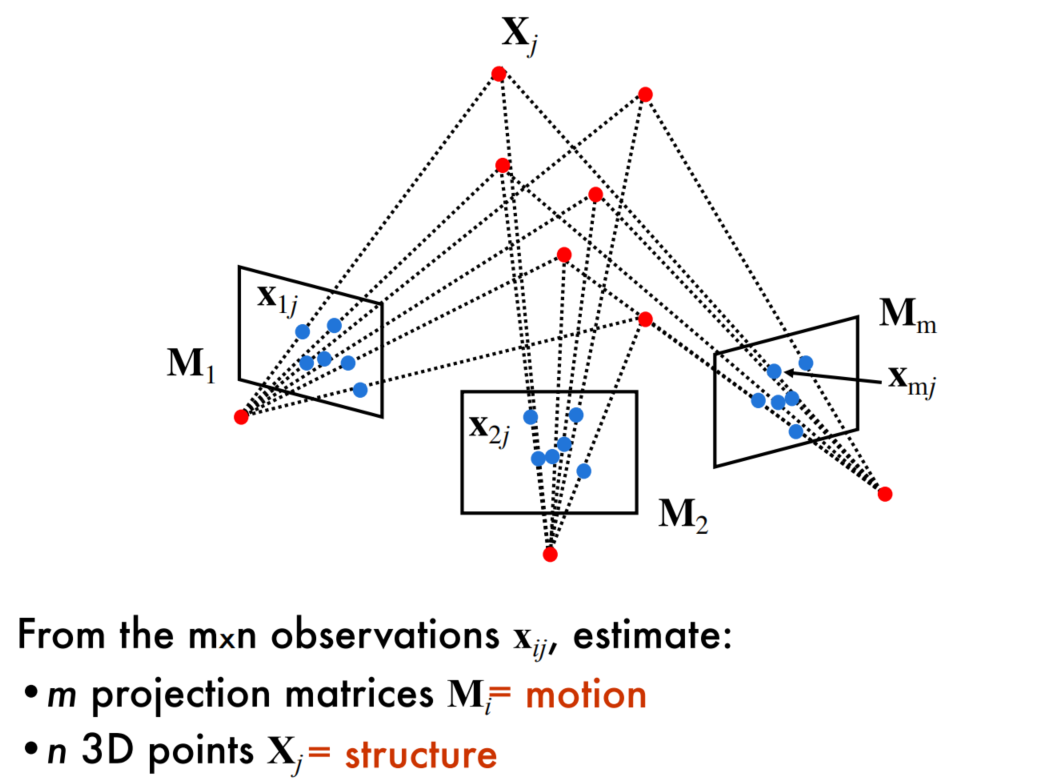
The Structure-from-Motion Problem

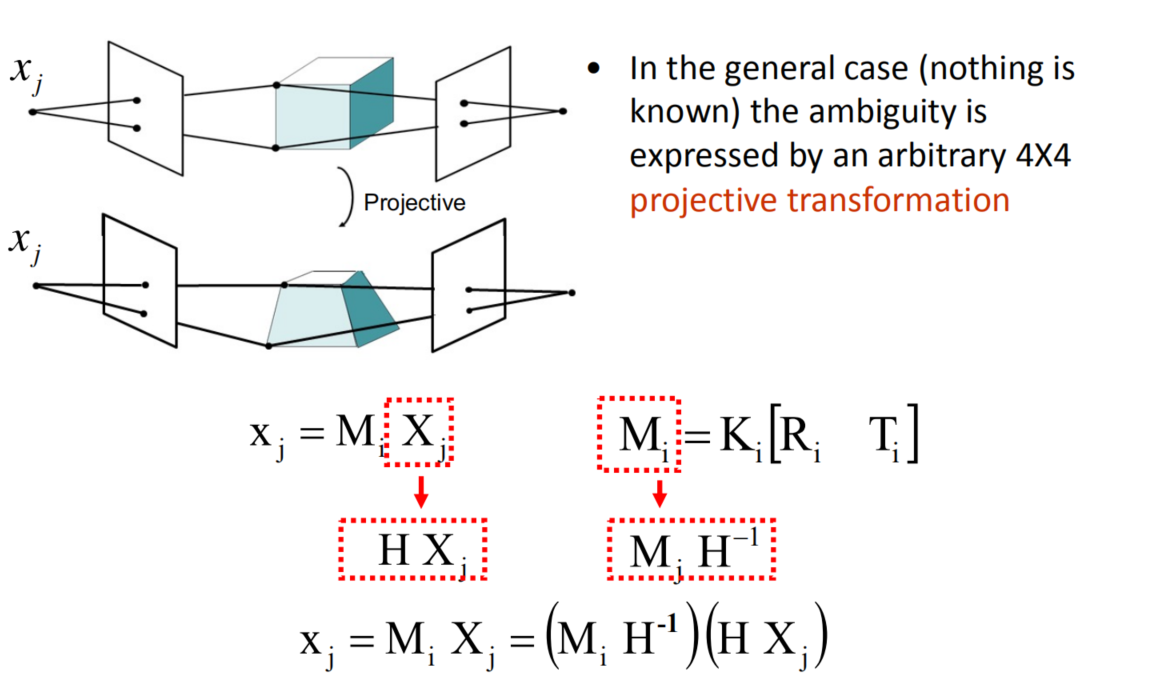
Projective Ambiguity
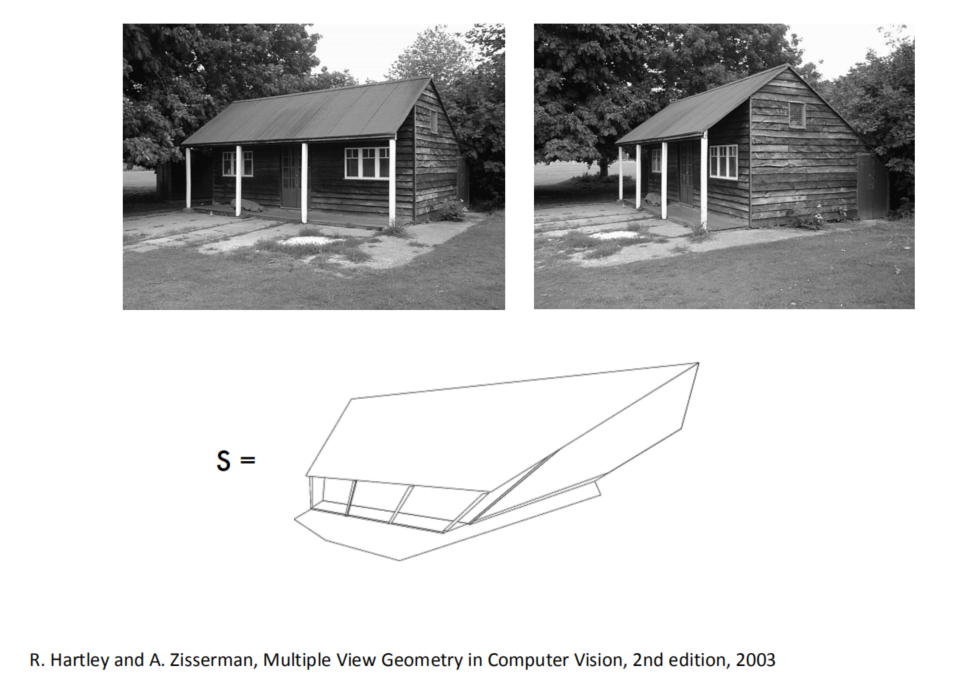
Metric reconstruction (upgrade)
Structure from Motion methods
- Recovering structure and motion up to perspective ambiguity
- Algebraic approach (by fundamental matrix)
- Factorization method (by SVD)
- Bundle adjustment
- Resolving the perspective ambiguity
疑问
Q:如何理解“If the cameras are not calibrated, cameras and points can only be recovered up to a 4x4 projective (where the 4x4 projective is defined up to scale)”
A:感觉这里说的是,因为不知道相机的内参,缺少了约束条件,最终恢复的场景和实际的场景差了一个投影变换。比如,实际的motion应该是刚性变换,但我们因为不知道相机内参,只能恢复成投影变换,就像”Projective Ambiguity“这个部分一样。但为什么知道相机内参之后能够恢复到刚性变换呢?
这里应该是知道内参之后可以把$M$求出来,这样$X$也确定了,就消除歧义了。
Q:这里的未知量数目为$11m+3n-15$,其中的$-15$是怎么来的?
A:TODO(我发现,在cs231a winter1415的课程中,ppt说这里的未知数是$11m+3n-16$,我猜这个应该是和projective transformation有关系,它刚好16个数,然后15个未知量;可能这个值在这里求不出,或者在这里不用求,然后只能用其他手段求解,比如self calibration?)
Recovering structure and motion up to perspective ambiguity
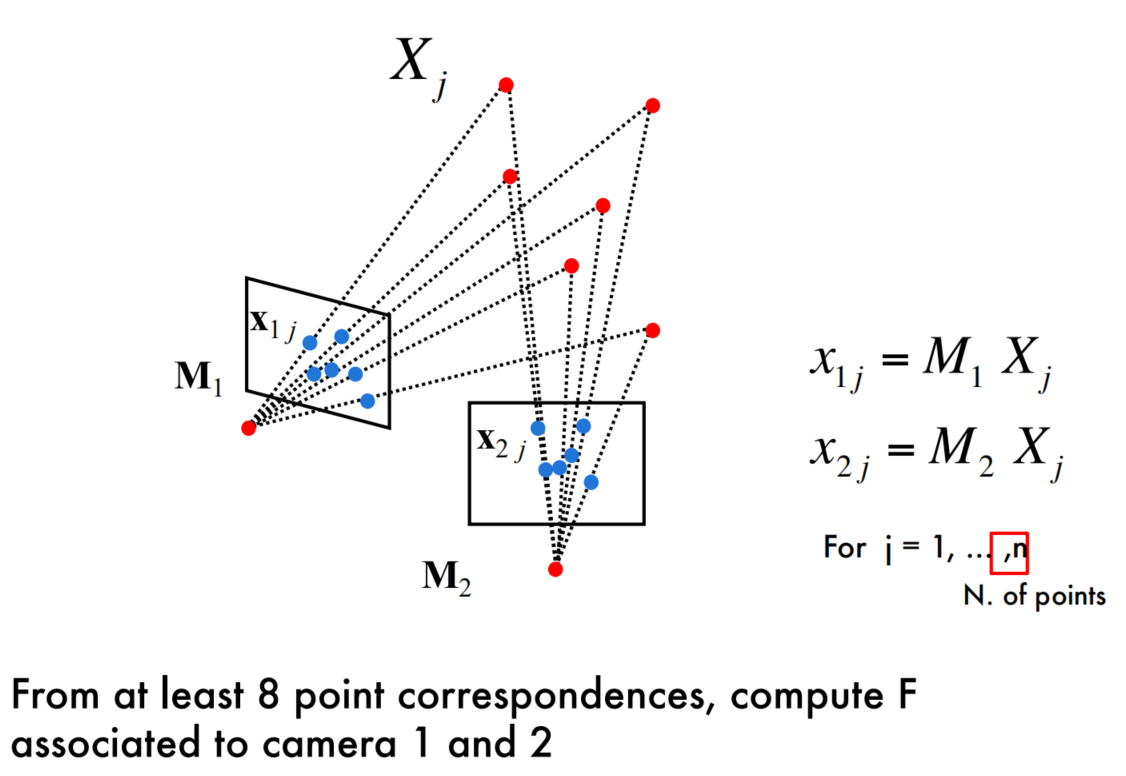
Algebraic approach (2-view case)
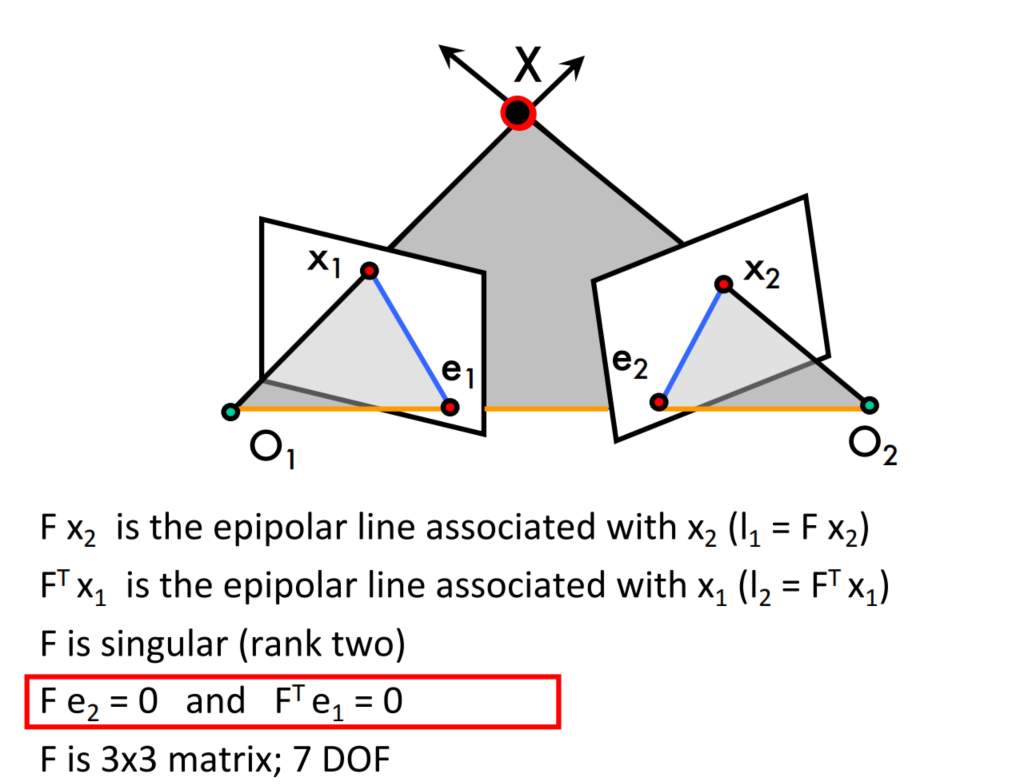
Compute the fundamental matrix F from two views
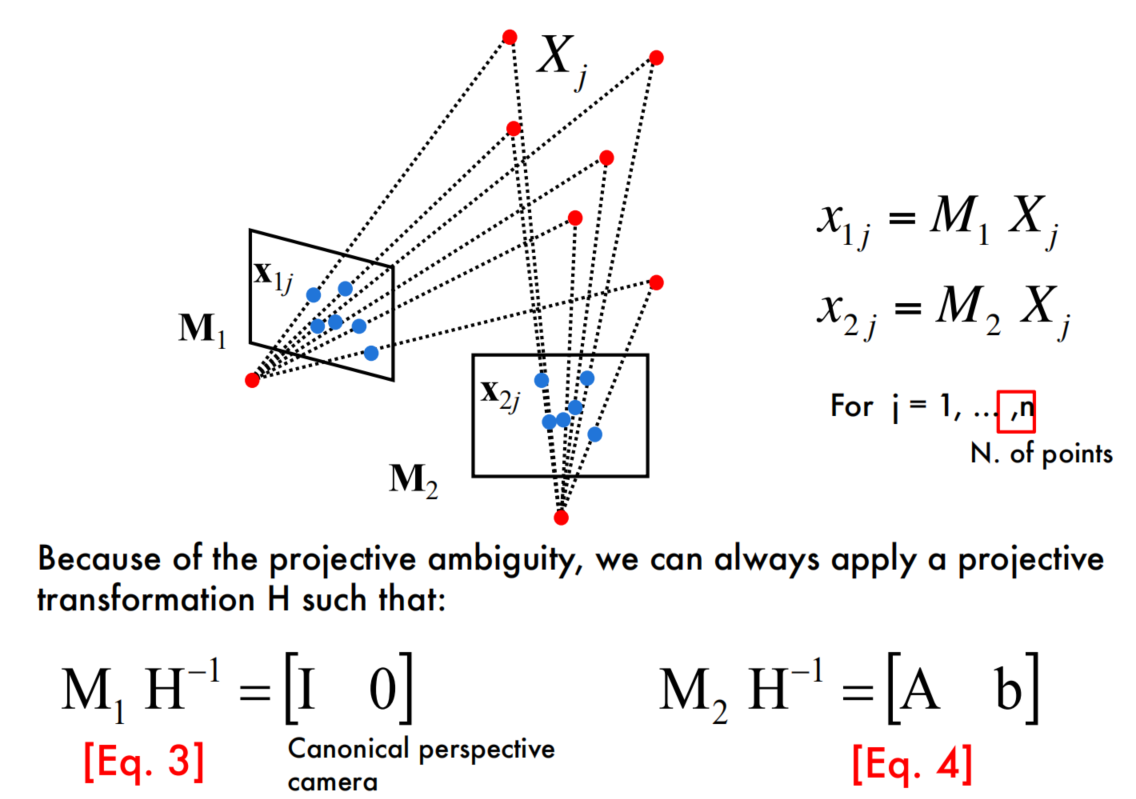
Use F to estimate projective cameras

Cross product as matrix multiplication
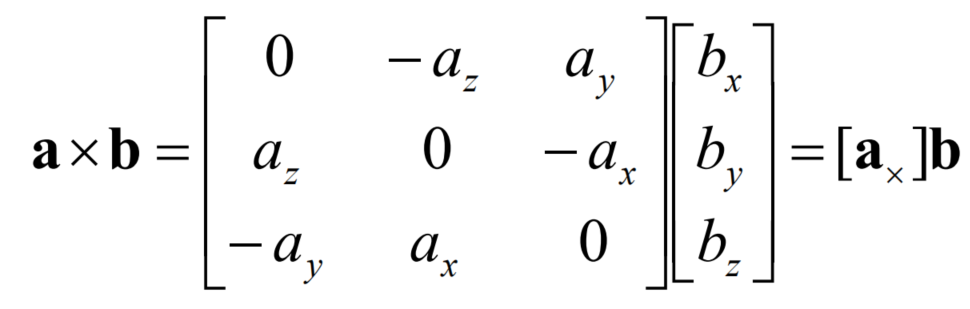

Compute cameras


Interpretation of b
回顾lecture5介绍的Epipolar Constraint

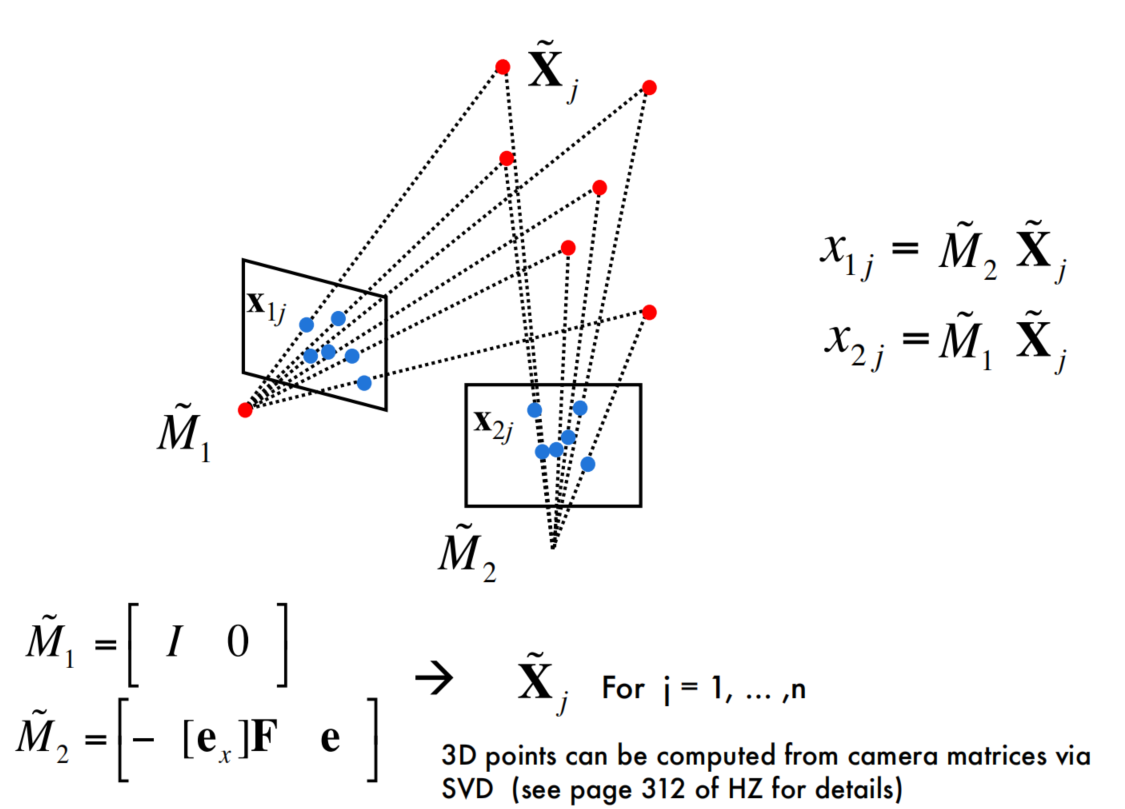
Use these cameras to triangulate and estimate points in 3D
Triangulation
Algebraic approach: the N-views case
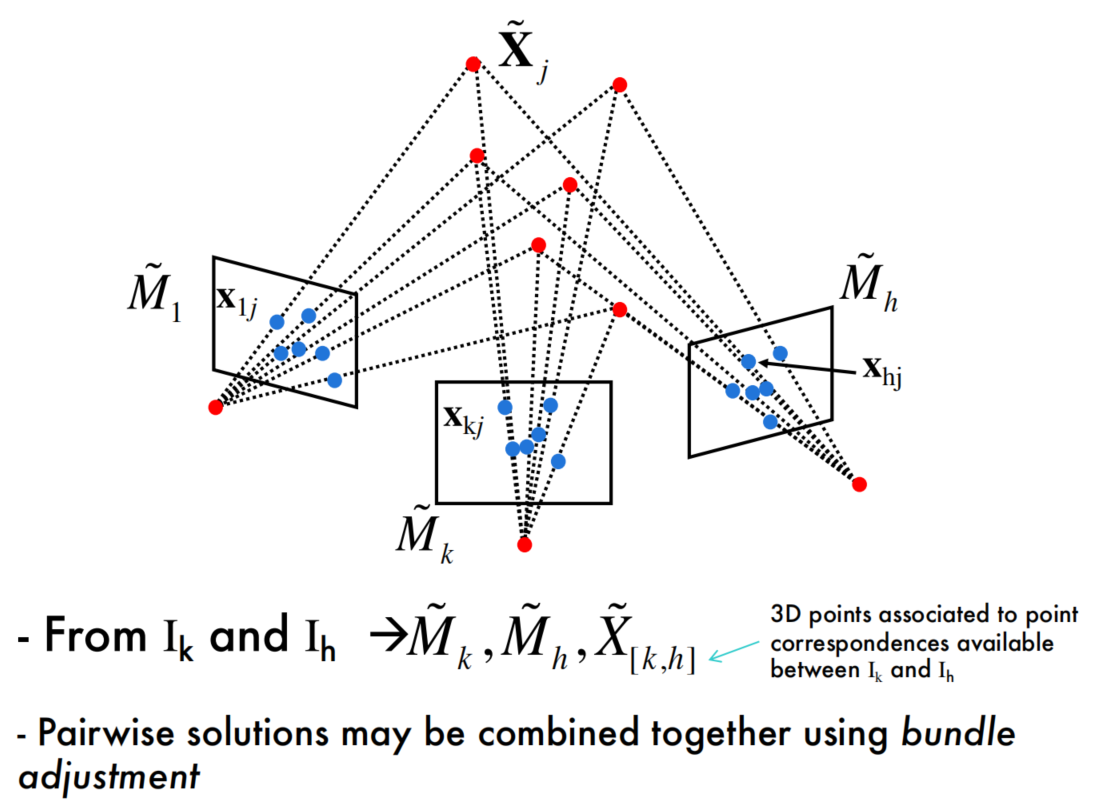
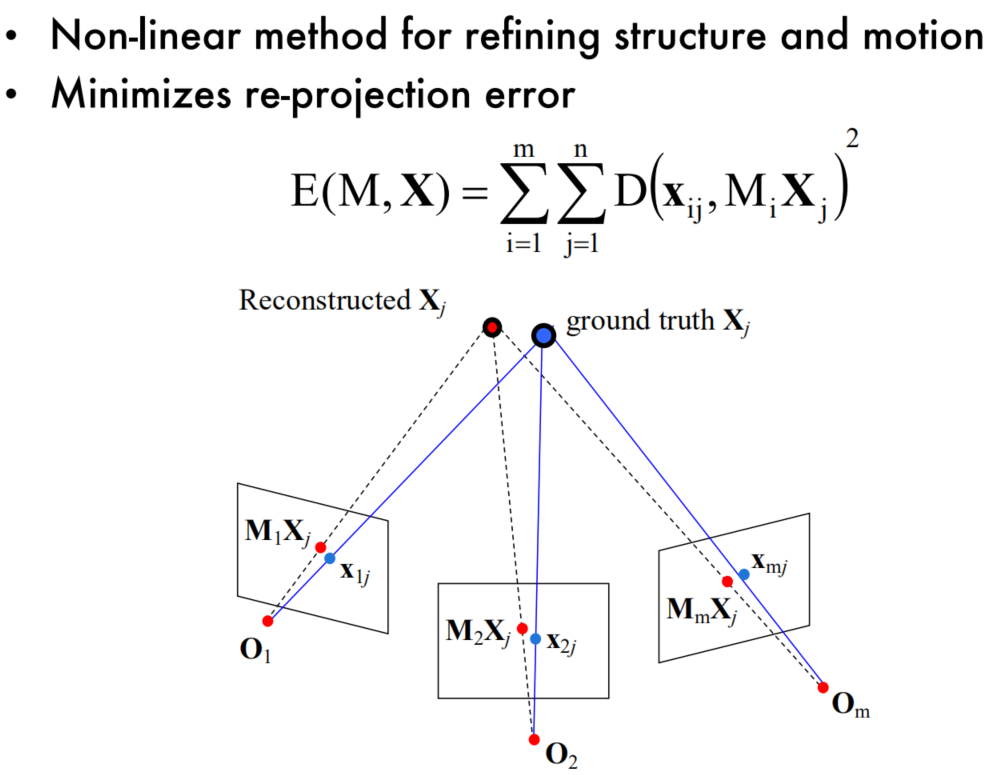
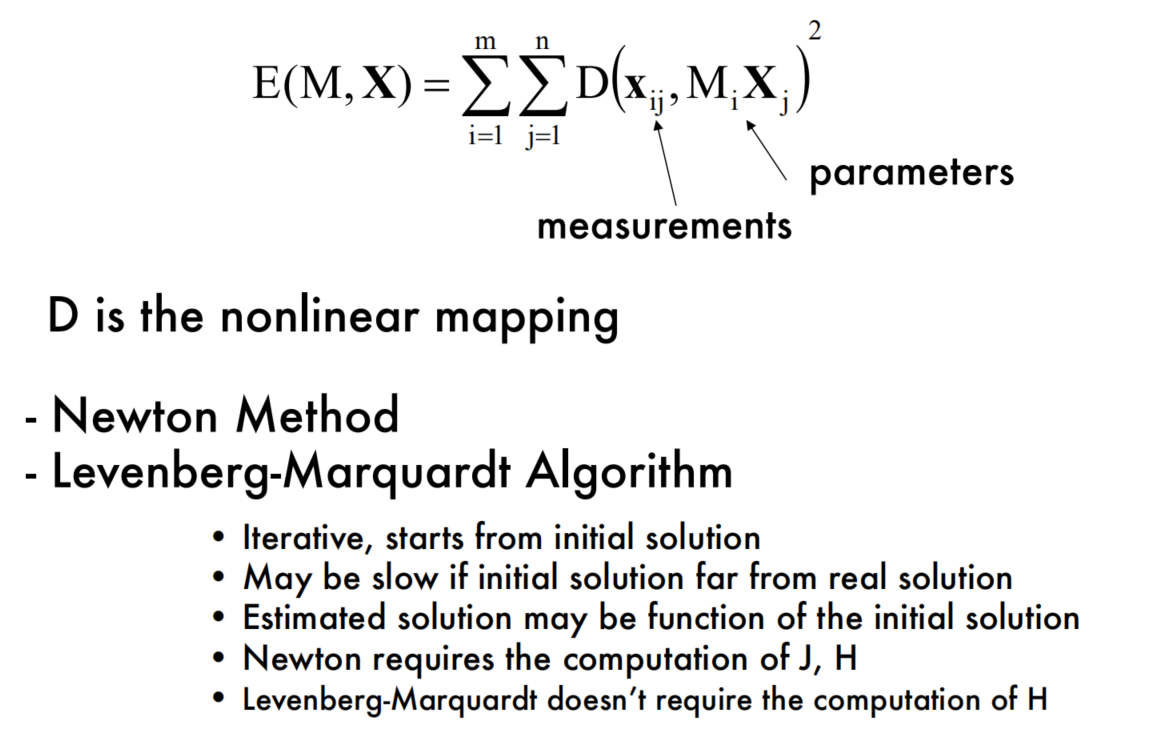
Bundle adjustment
Limitations of the approaches so far

About BA
General Calibration Problem
Advantages & Limitations

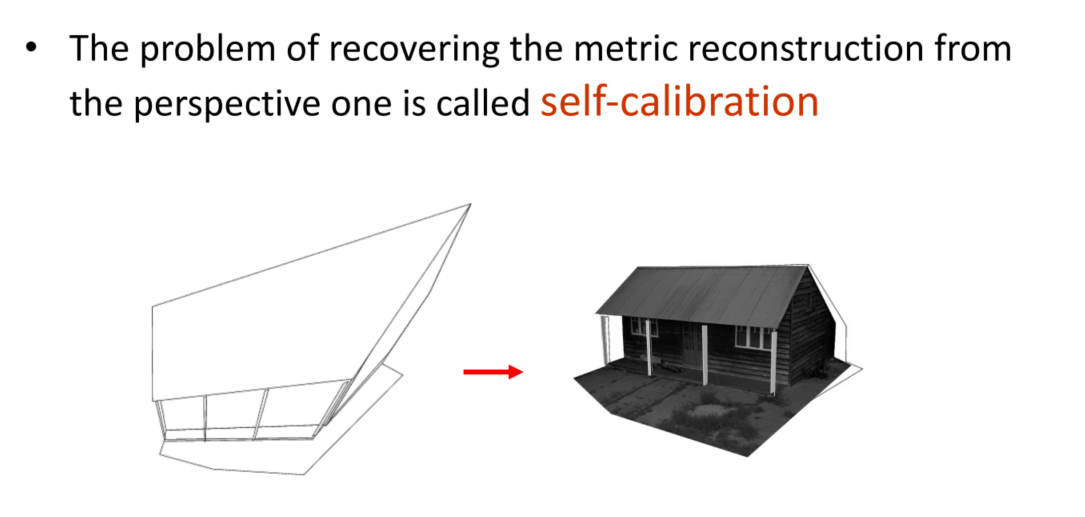
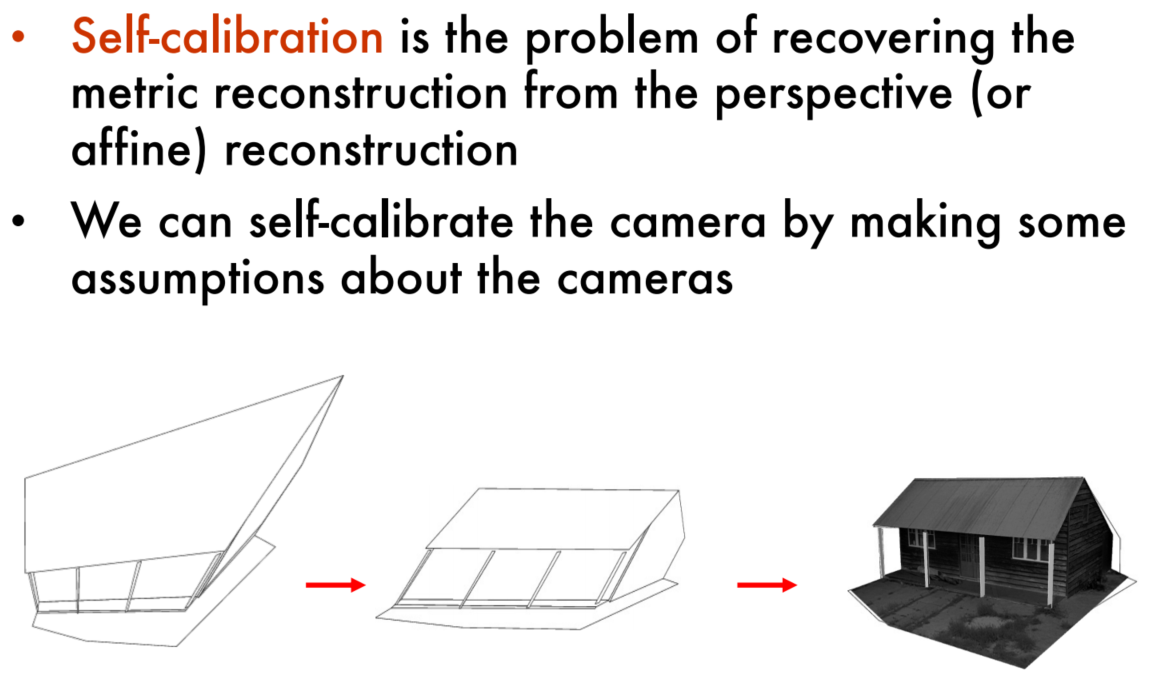
Resolving the perspective ambiguity: Self-calibration
About Self-calibration
Several approaches

Direct approach

Projections of conics across views
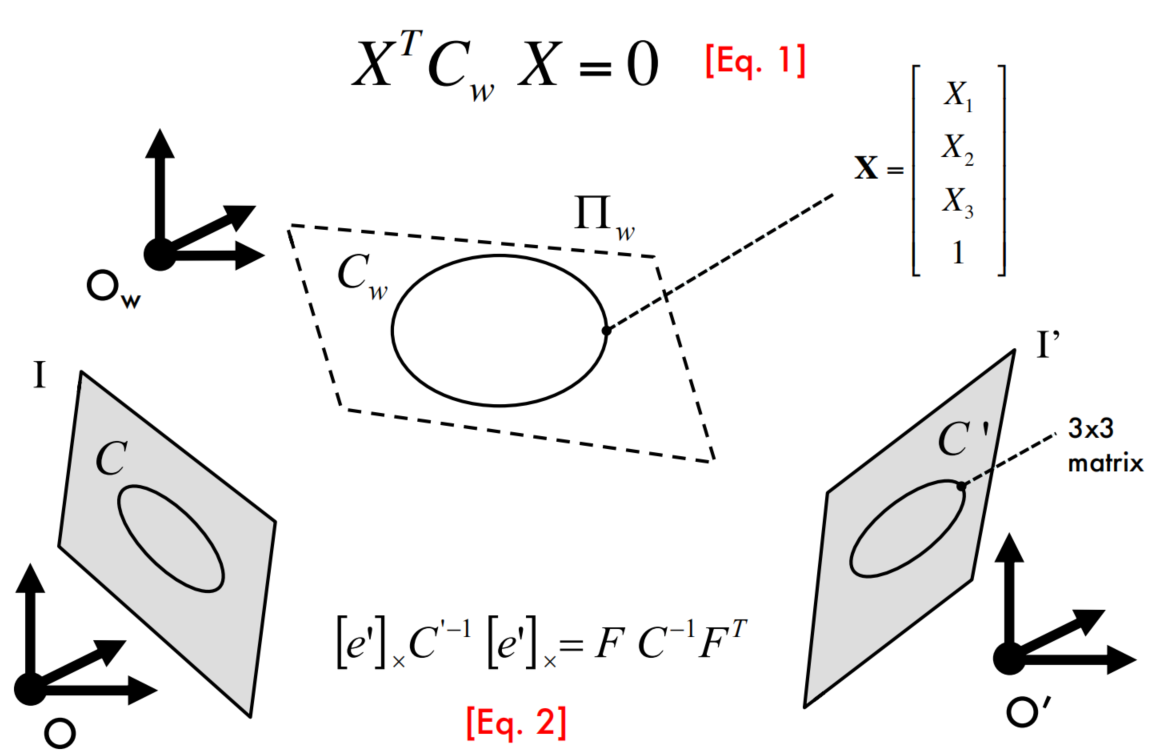
Projection of absolute conics across views
From lecture 4, [HZ] page 210, sec. 8.5.1
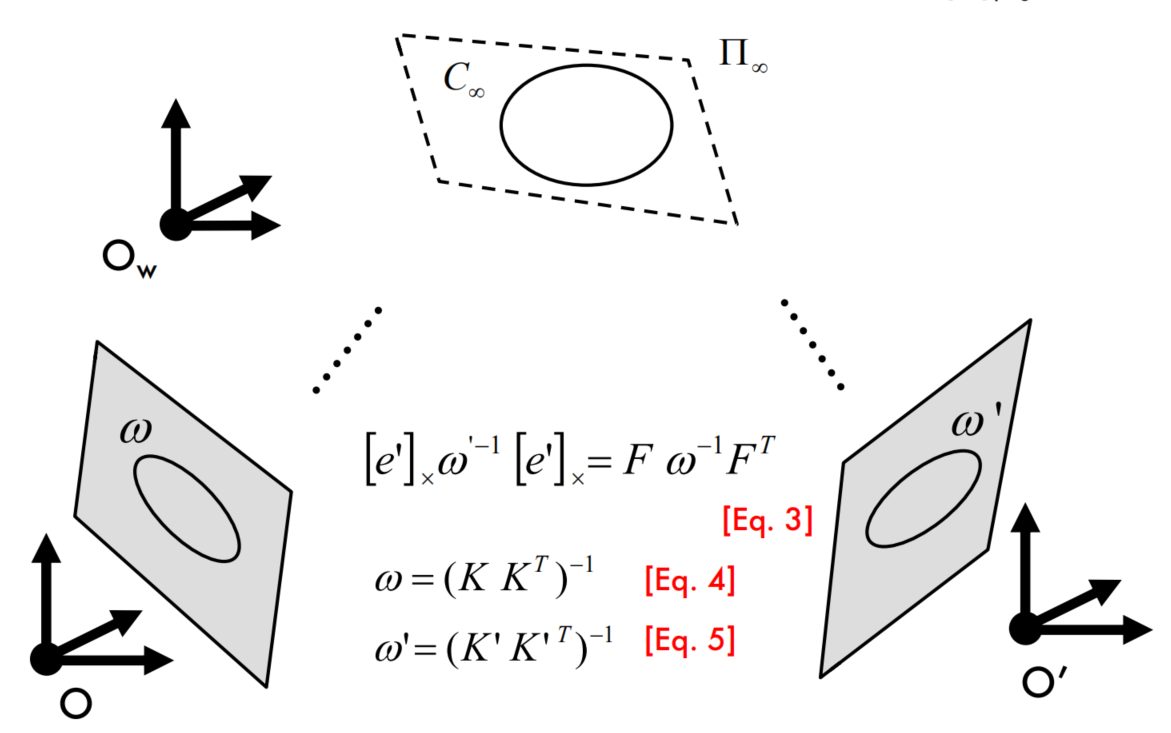
Kruppa equations
[Faugeras et al. 92] From [HZ] page 471

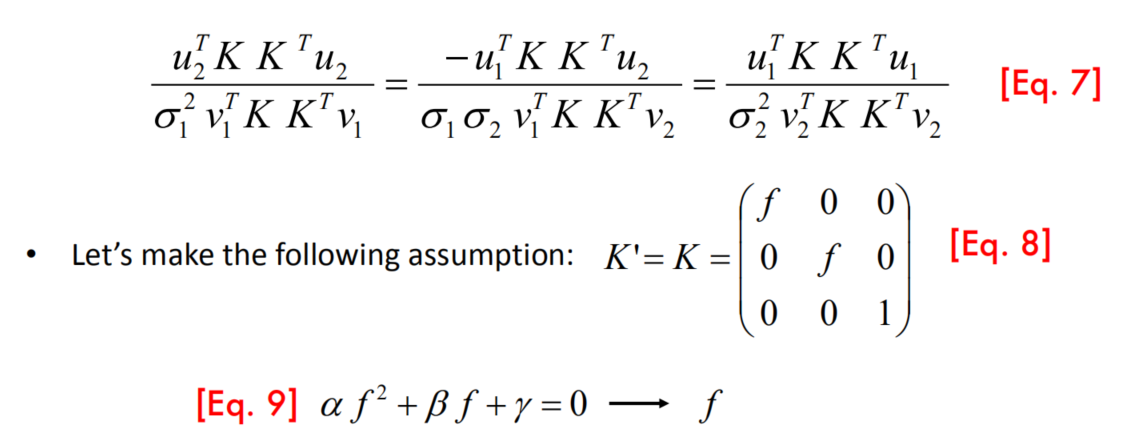
Advantages & Limitations
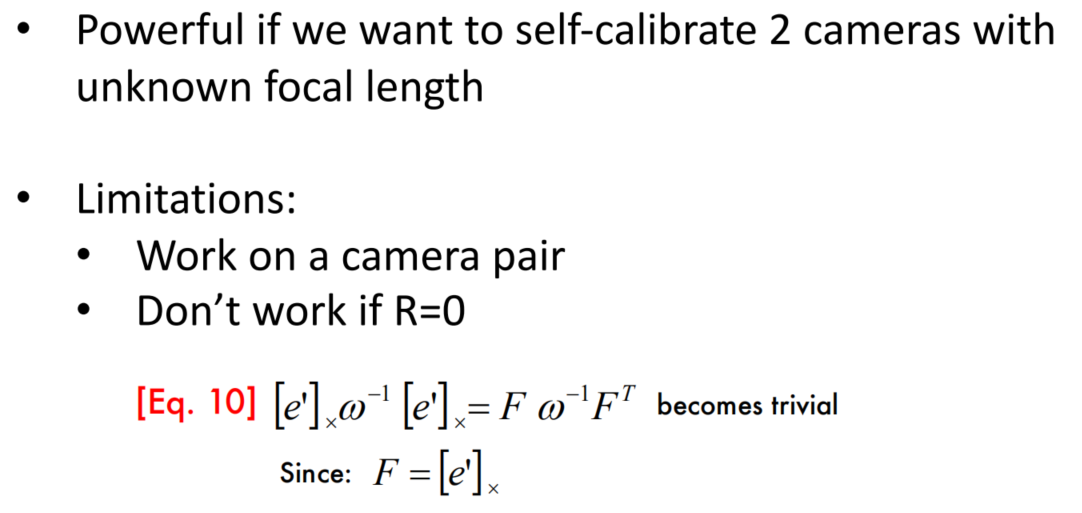
疑问
Q:这里的矩阵$F$表示什么?
A:TODO
Algebraic approach (Multi-view approach)


Art of self-calibration:
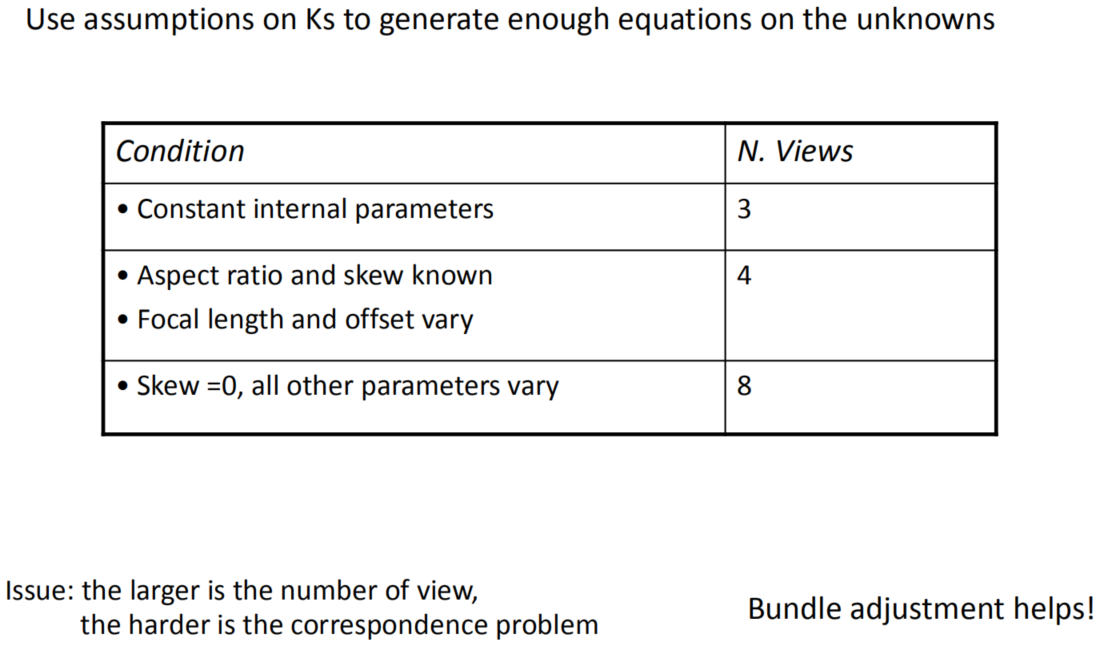
Inject information about the camera during the bundle adjustment optimization