CS231A Lecture 6：Stereo Systems

Reading:

[HZ] Chapter: 9 “Epip. Geom. and the Fundam. Matrix Transf.”

[HZ] Chapter: 18 “N view computational methods”

[FP] Chapters: 7 “Stereopsis”

[FP] Chapters: 8 “Structure from Motion”

Rectification

Epipolar geometry

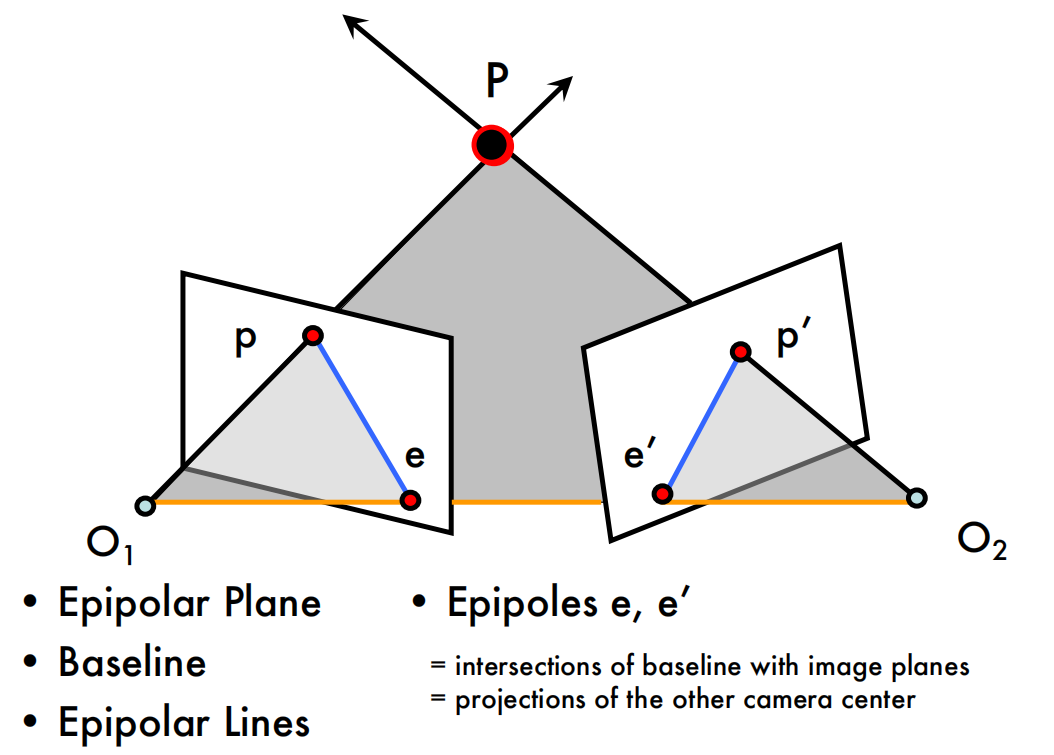
Epipolar Constraint

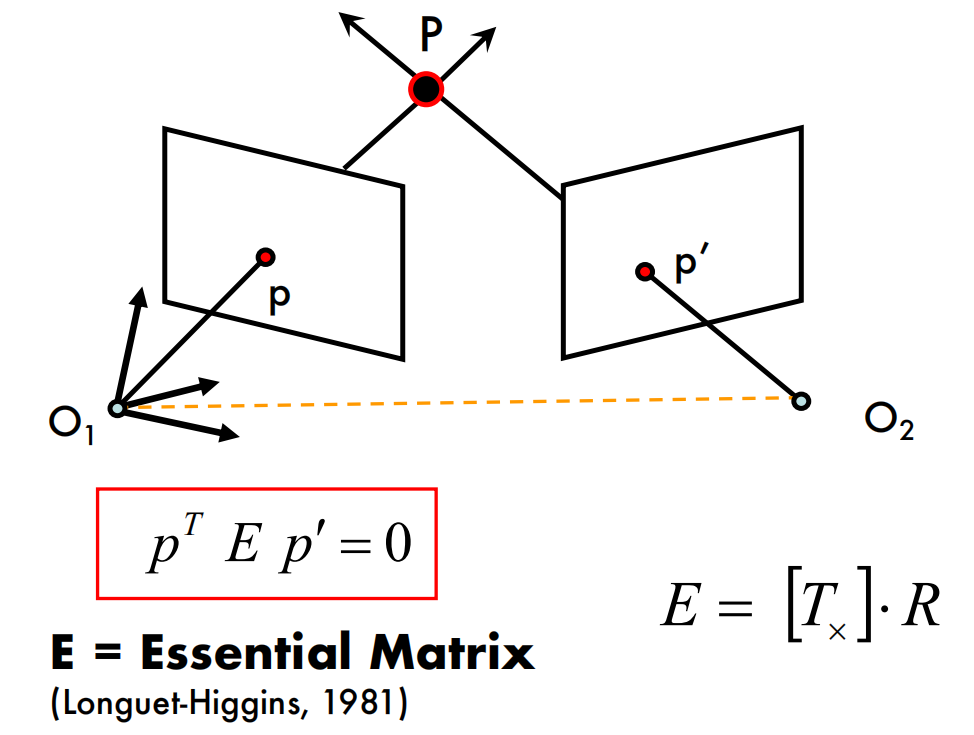
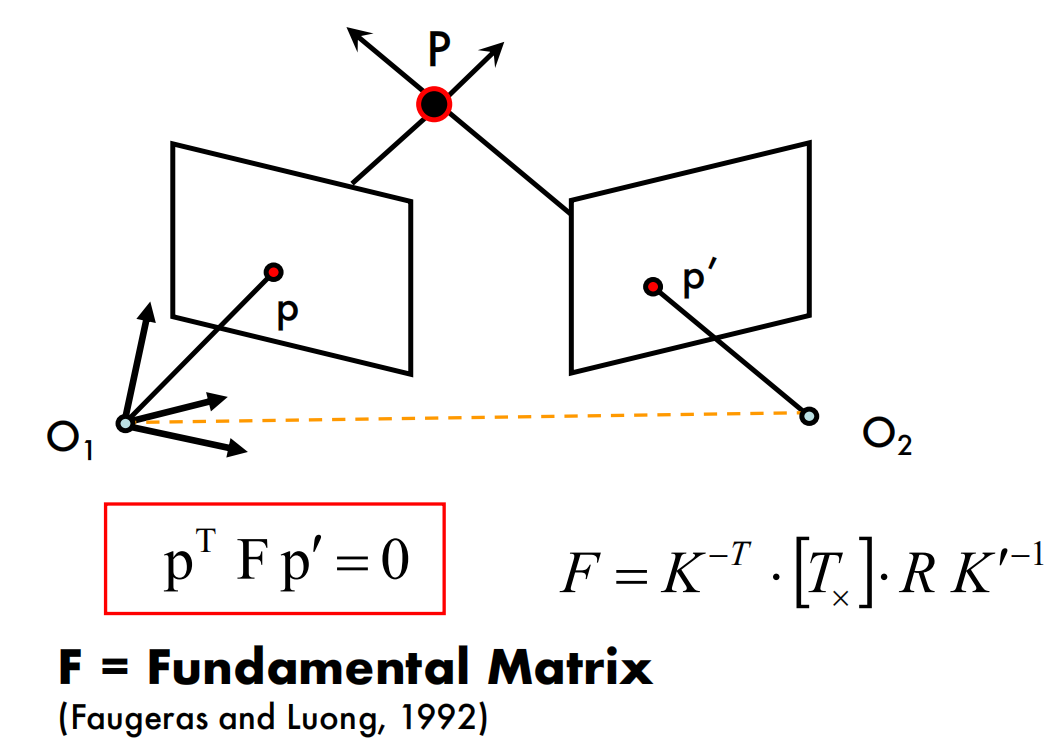
Parallel image planes

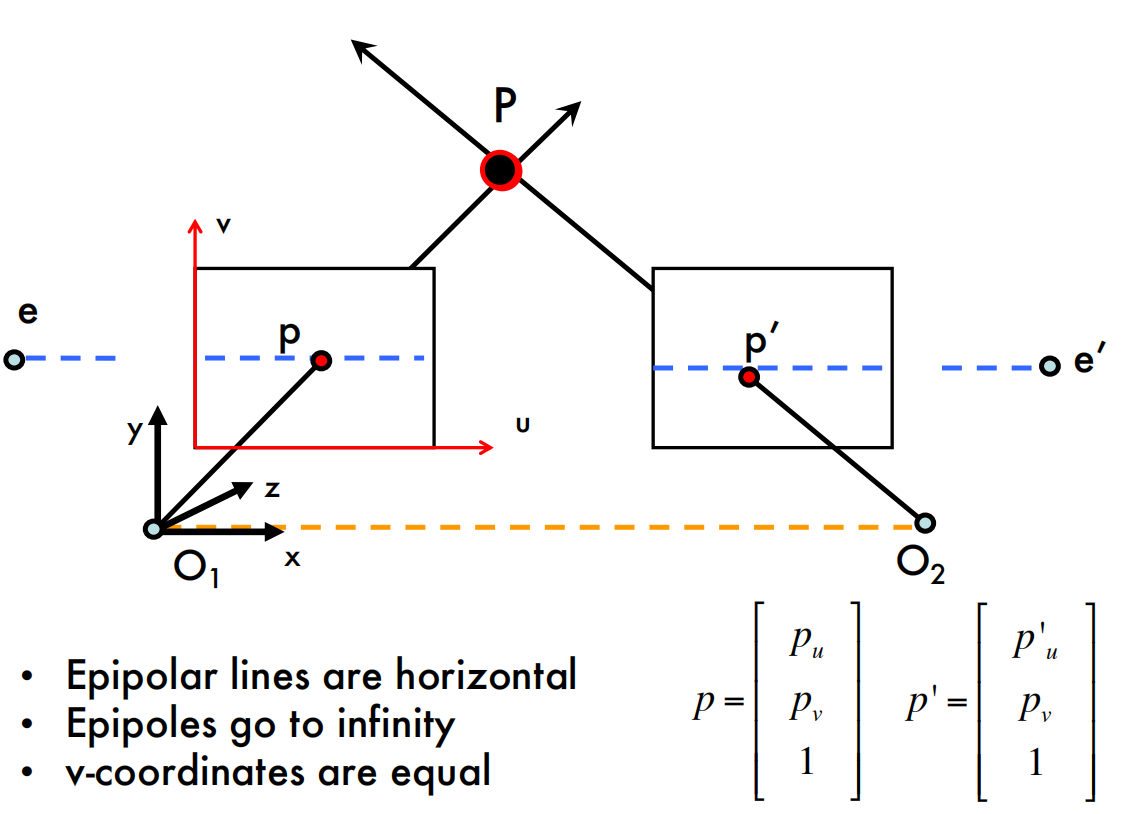
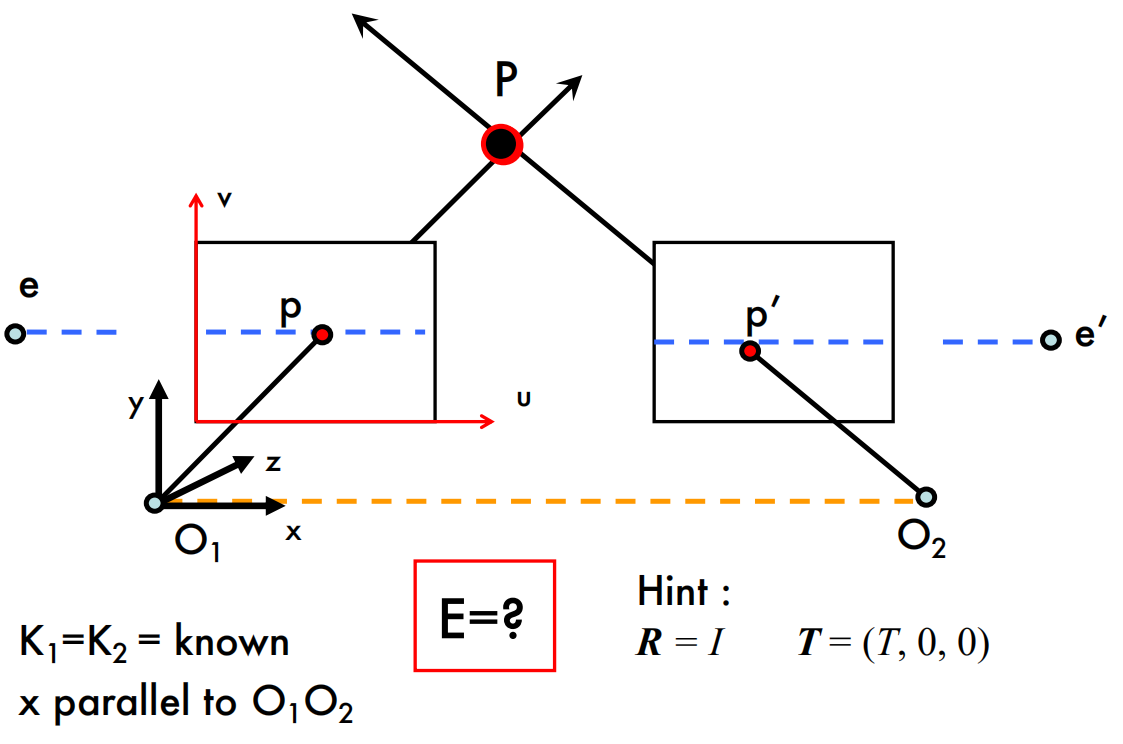
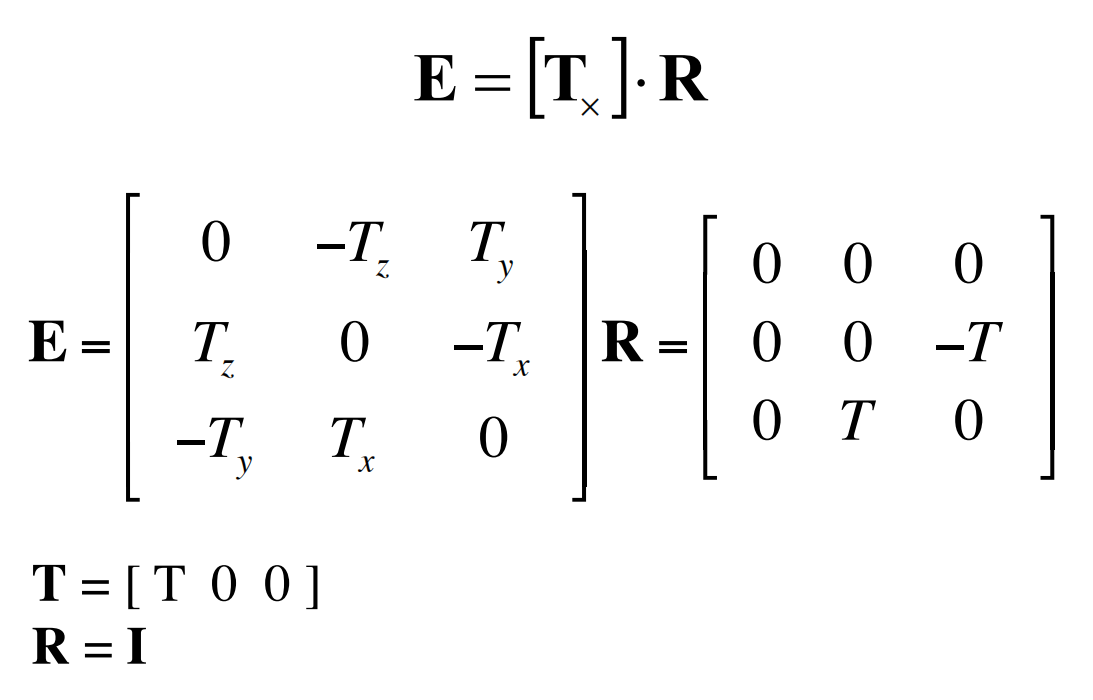
Essential matrix for parallel images

What are the directions of epipolar lines?

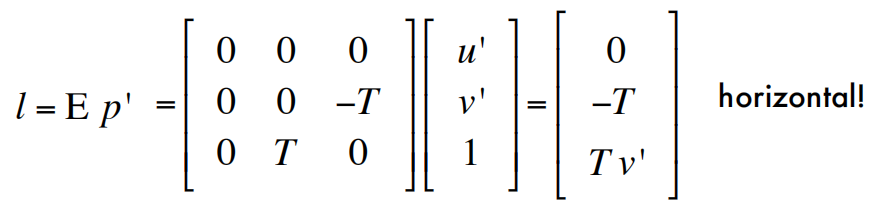
How are p and p’ related?

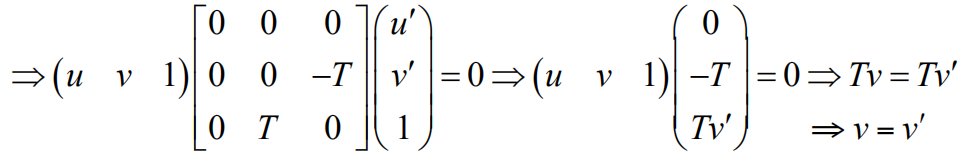
Rectification: making two images “parallel”

Rectification

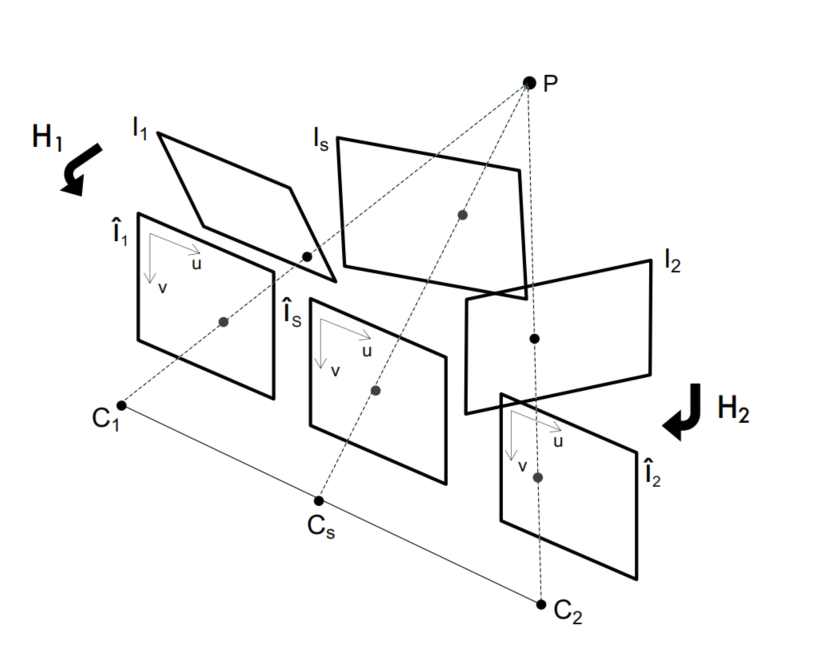
Example

Why it is useful?

• Epipolar constraint $\rightarrow v = v’$
• New views can be synthesized by linear interpolation

Why are parallel images useful?

• Makes triangulation easy

  

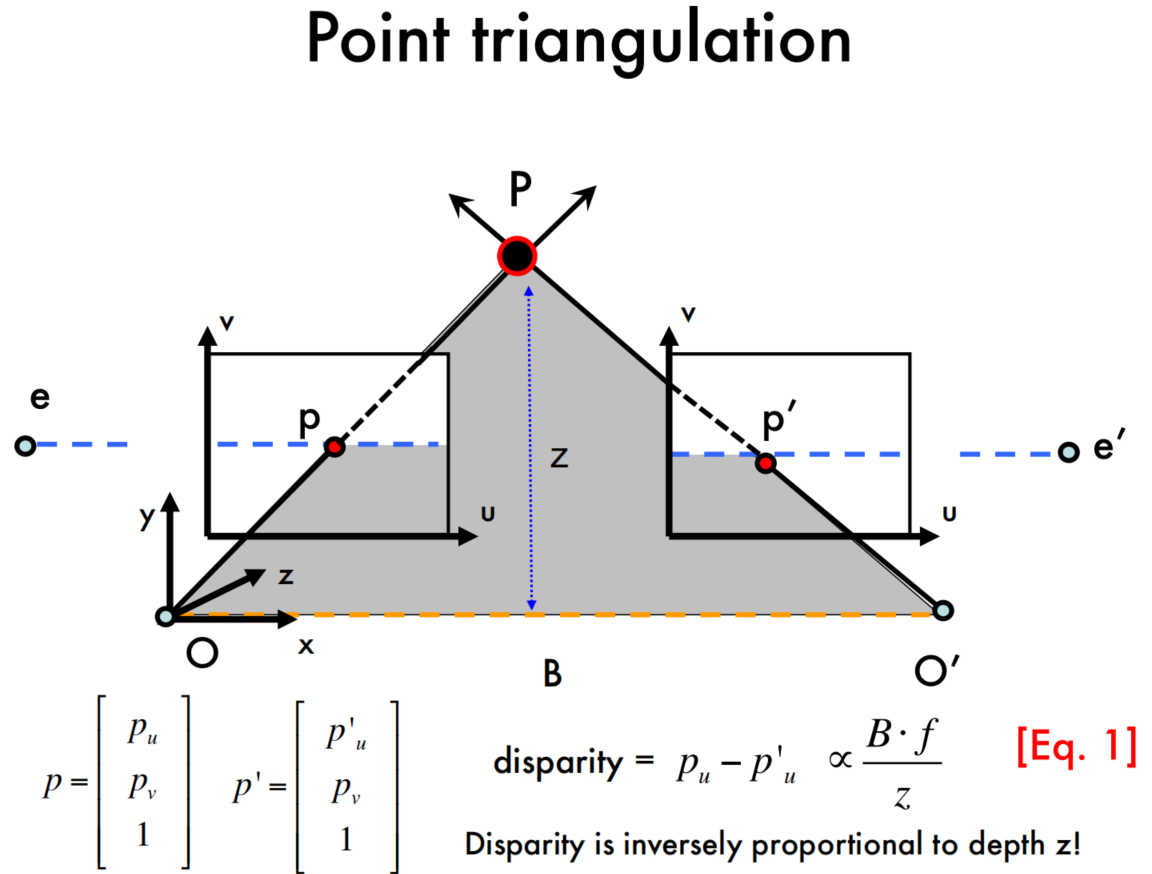
  这里有点类似双目相机的模型了。

• Makes the correspondence problem easier

Correspondence problem

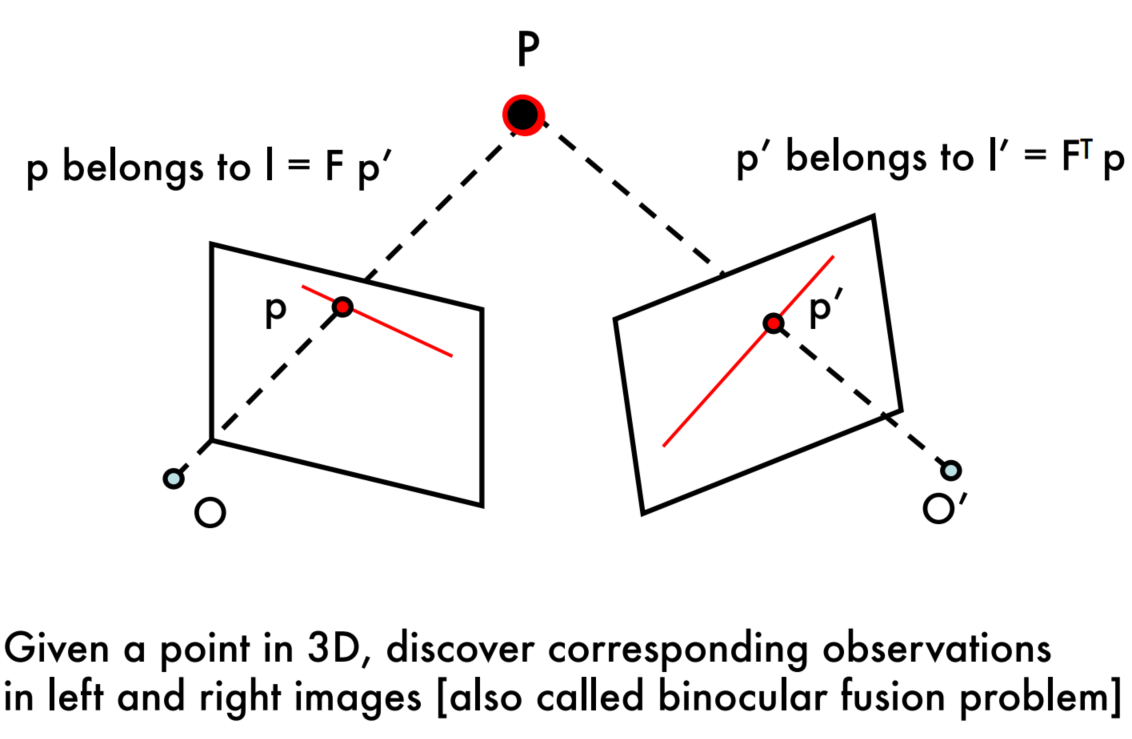
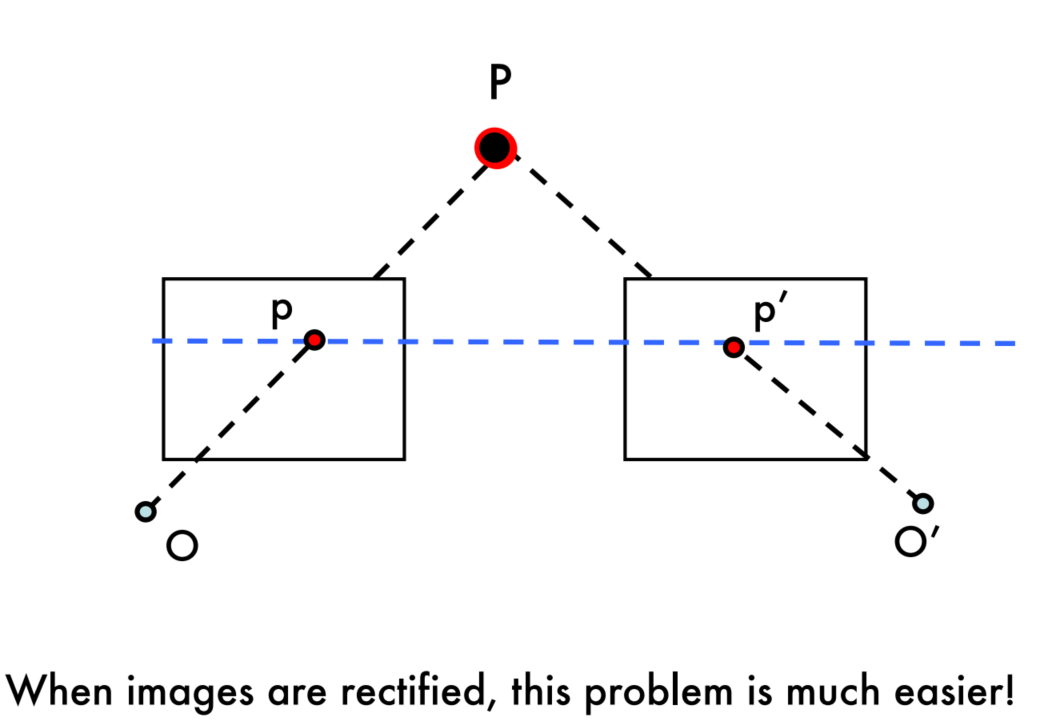
Correlation Methods

A Simple Idea

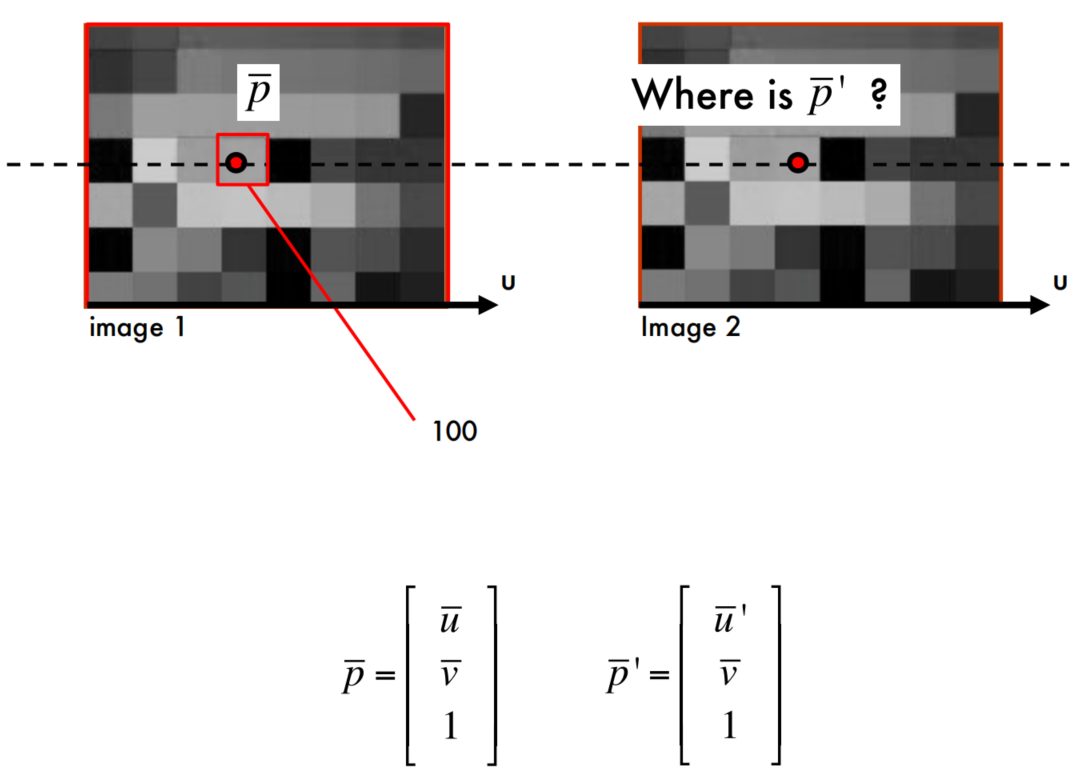
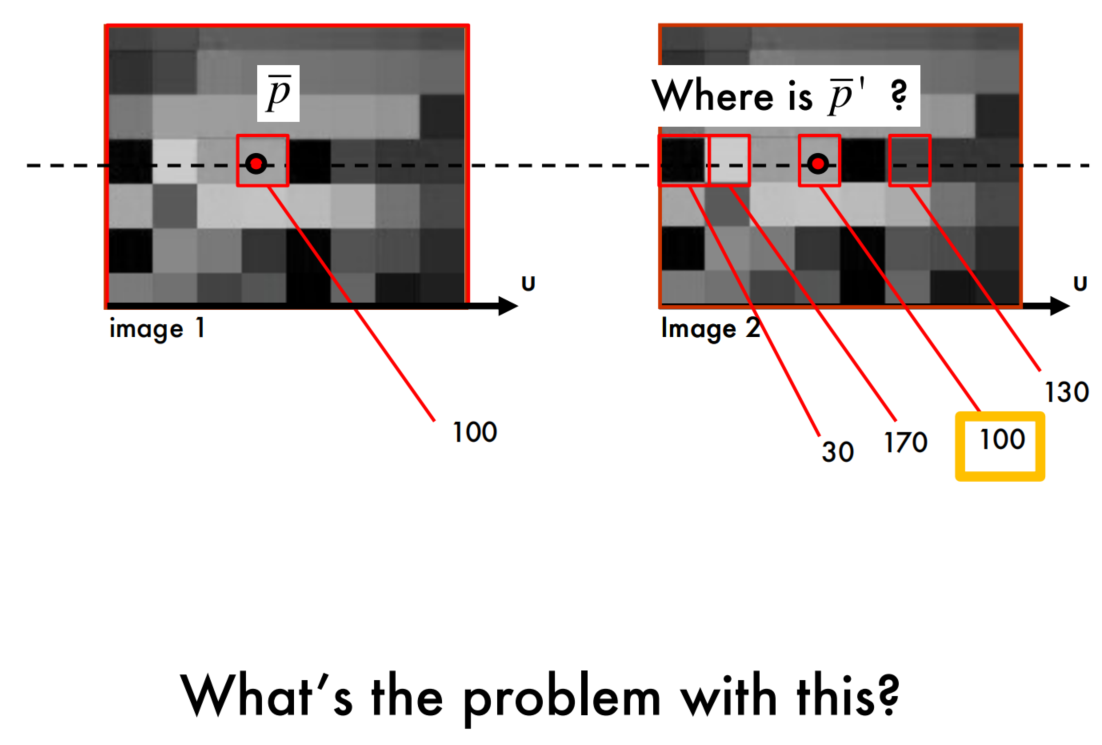
思考：

这里的问题是，只检查一个像素点，没有考虑到像素值相同的点可能比较多，很容易导致错误匹配。

Window-based correlation

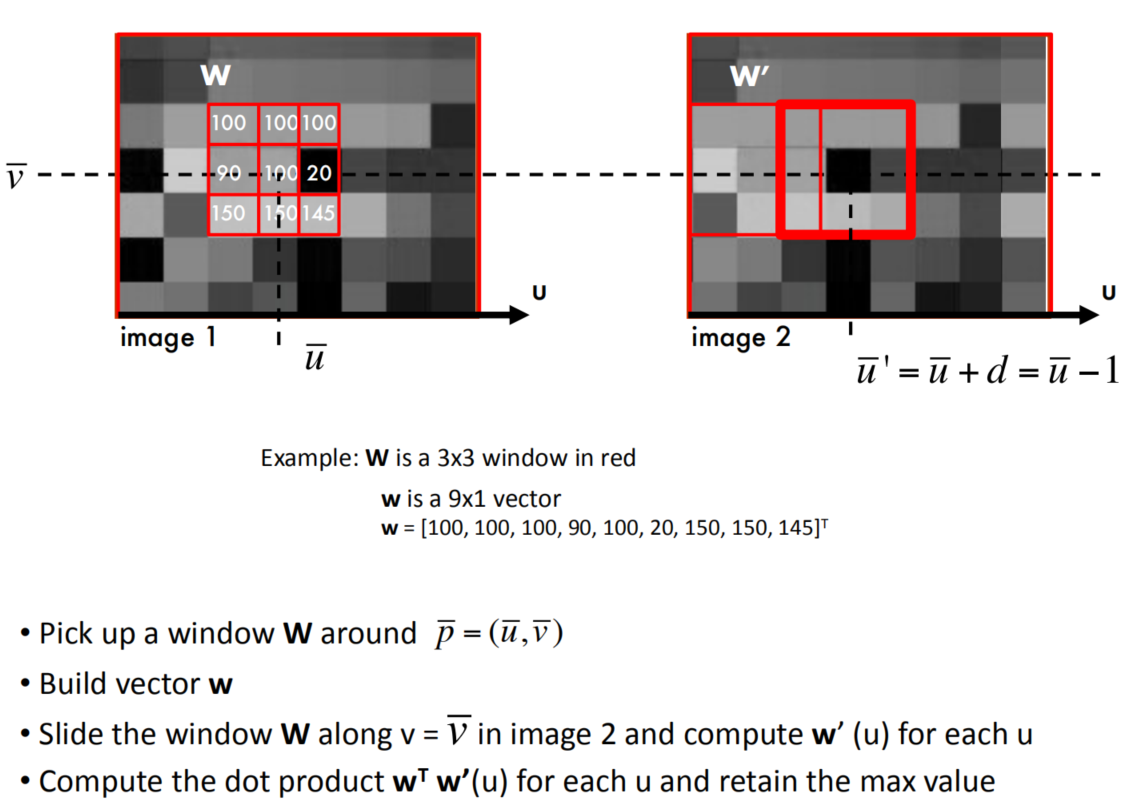
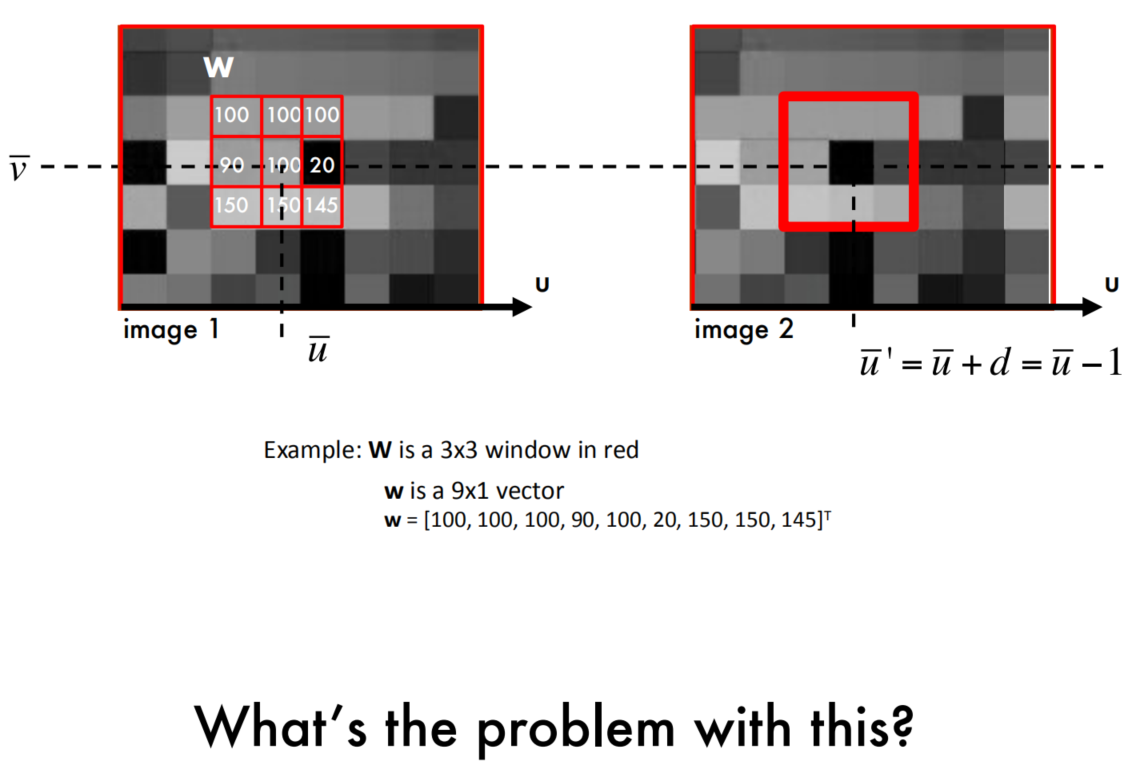
思考：

这里的问题是，只计算两个矩阵的点乘，并且认为最大值是匹配的最好的。

这样处理很容易受到光照或者曝光的影响，如下所示。

Changes of brightness/exposure

Normalized cross-correlation

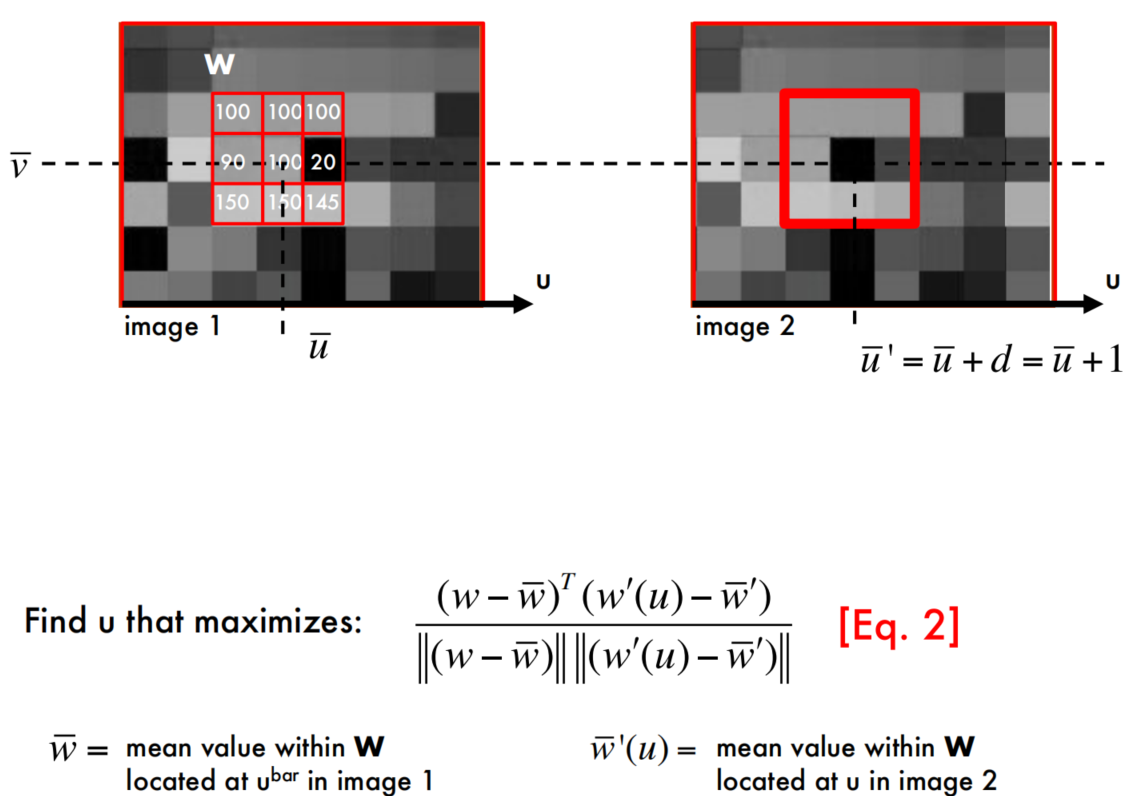
Effect of the window’s size

Issues

• Fore shortening effect

  

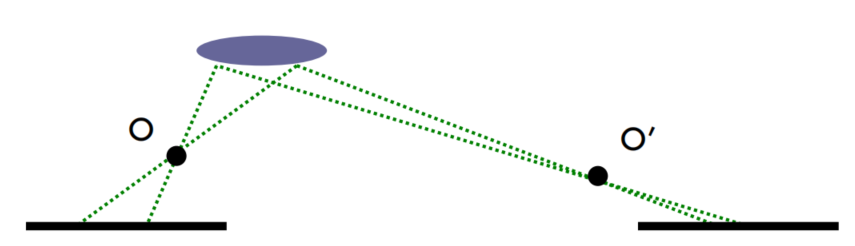
  这个网站把Fore shortening effect介绍的非常清楚：Foreshortening – What It Means and How to Paint It

  从上图中也可以看出，左边相机拍摄的物体很长，而右边因为距离较远就缩短了。前面几种算法在这里容易出问题，他们都是在一条水平线上查找固定大小的window，但是利用图像金字塔应该可以处理这种问题。

• Occlusions

  

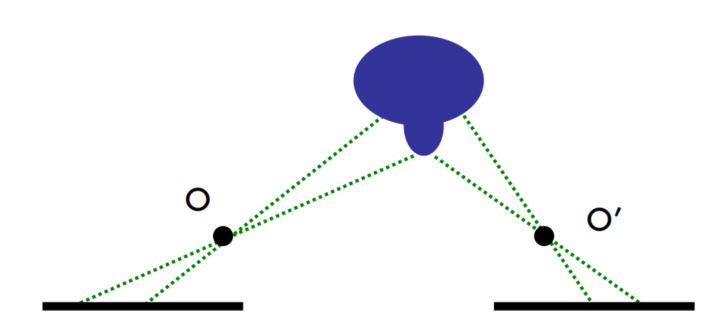
  因为遮挡导致两个相机观察的内容不一样。

• Base line trade-off

  

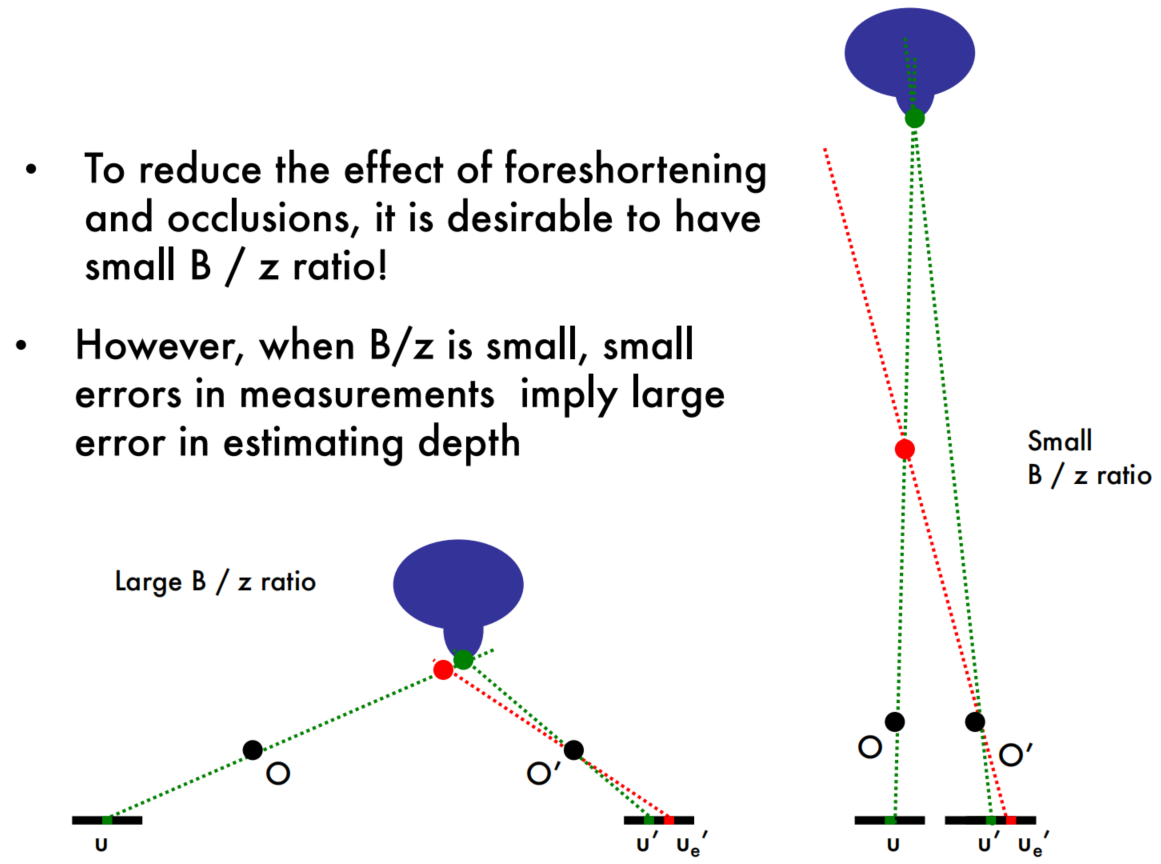
• Homogeneous regions

  

• Repetitive patterns

  

Correspondence problem is difficult!

Non-local constraints