CS231A Lecture 5:Epipolar Geometry
Reading:
[HZ] Chapter: 4 “Estimation – 2D perspective transformations
[HZ] Chapter: 9 “Epipolar Geometry and the Fundamental Matrix Transformation”
[HZ] Chapter: 11 “Computation of the Fundamental Matrix F”
[FP] Chapter: 7 “Stereopsis”
[FP] Chapter: 8 “Structure from Motion”
Why is stereo useful?
Recovering structure from a single view
Why is it so difficult?
Intrinsic ambiguity of the mapping from 3D to image (2D)
Triangulation
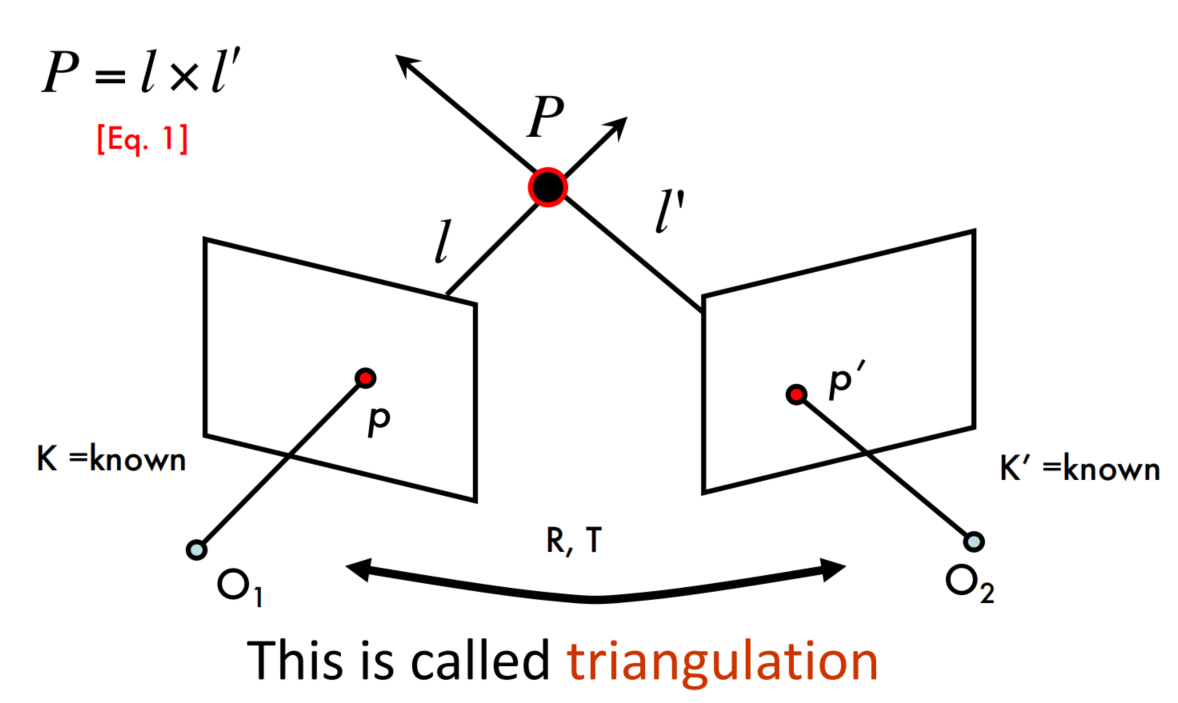
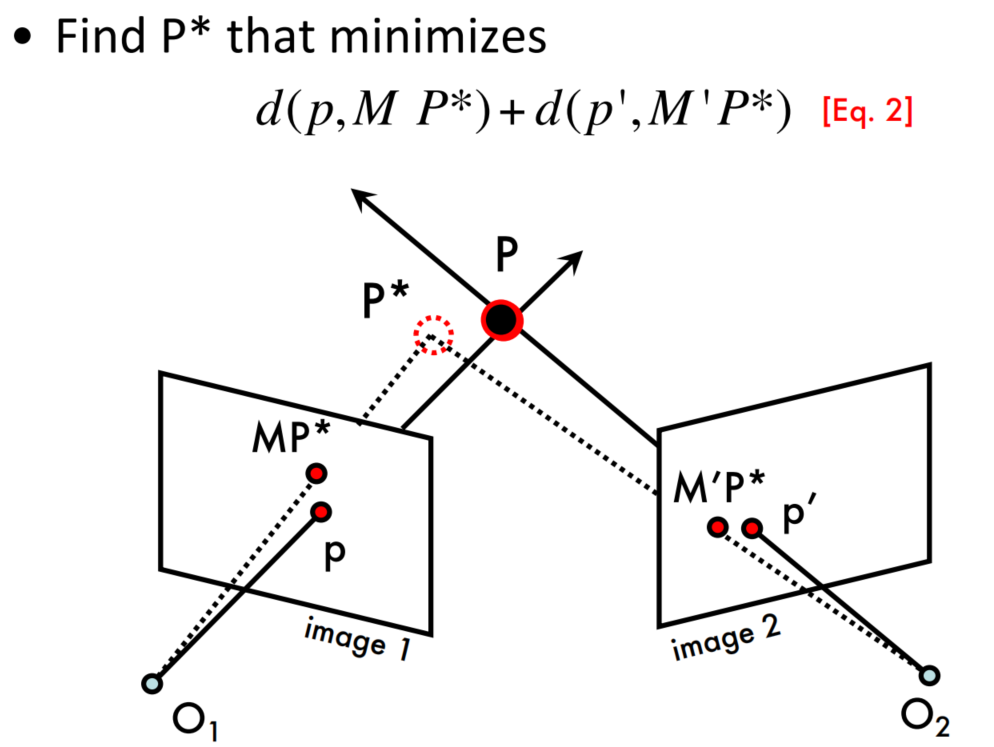
Multi (stereo)-view geometry

Epipolar geometry
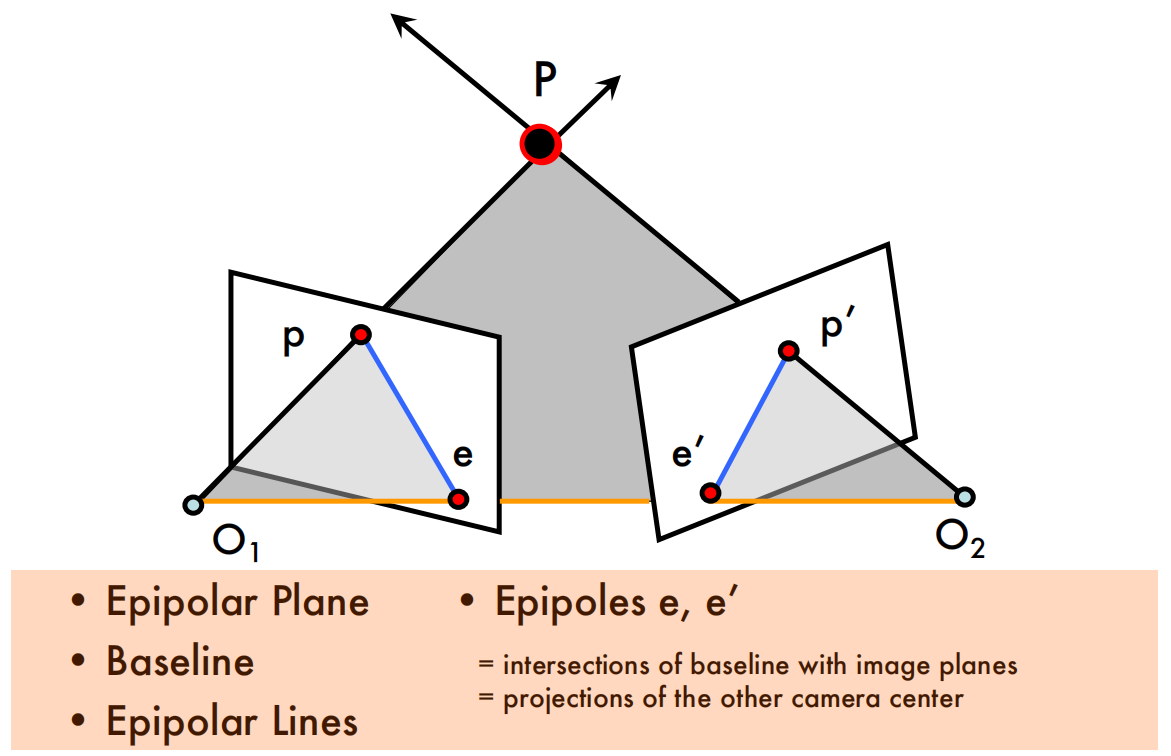
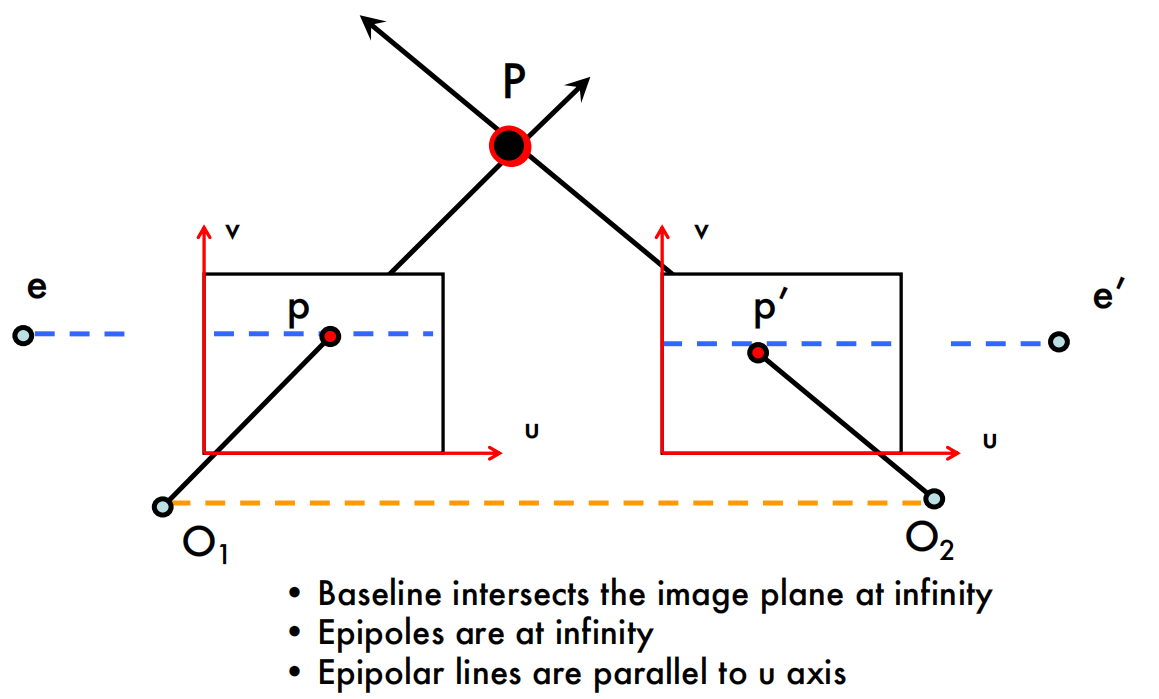
Example: Parallel image planes
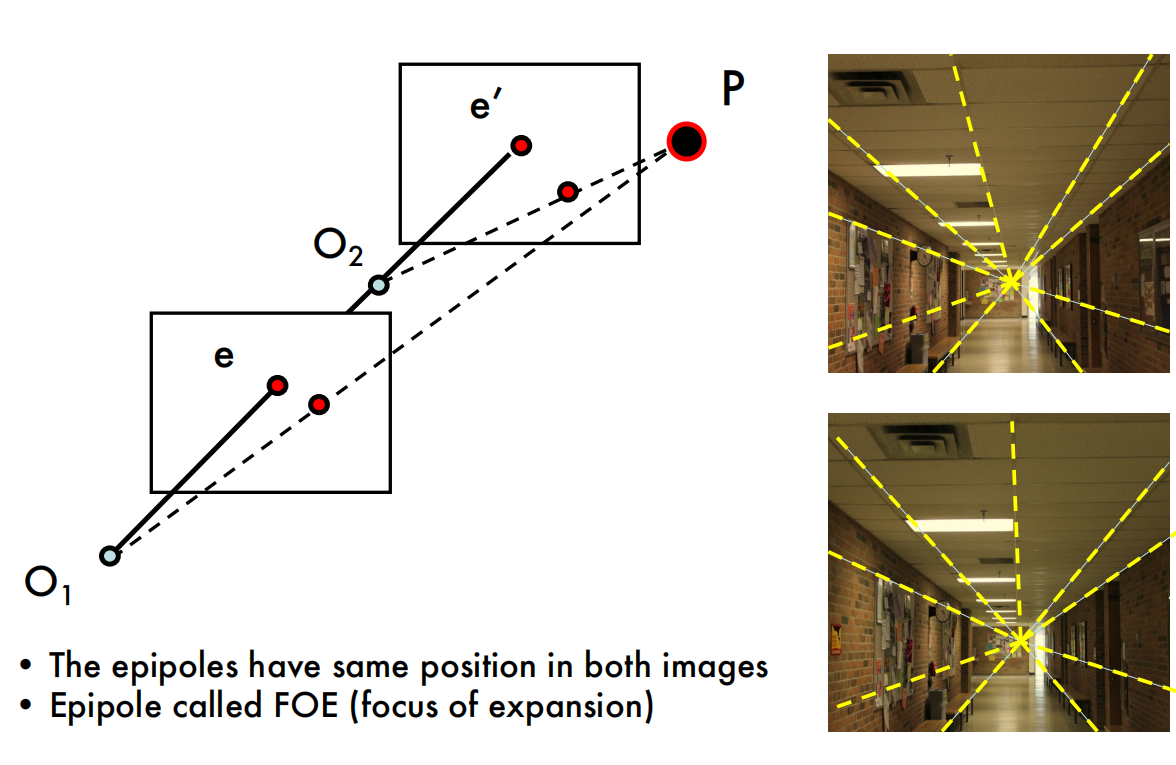
Example: Forward translation
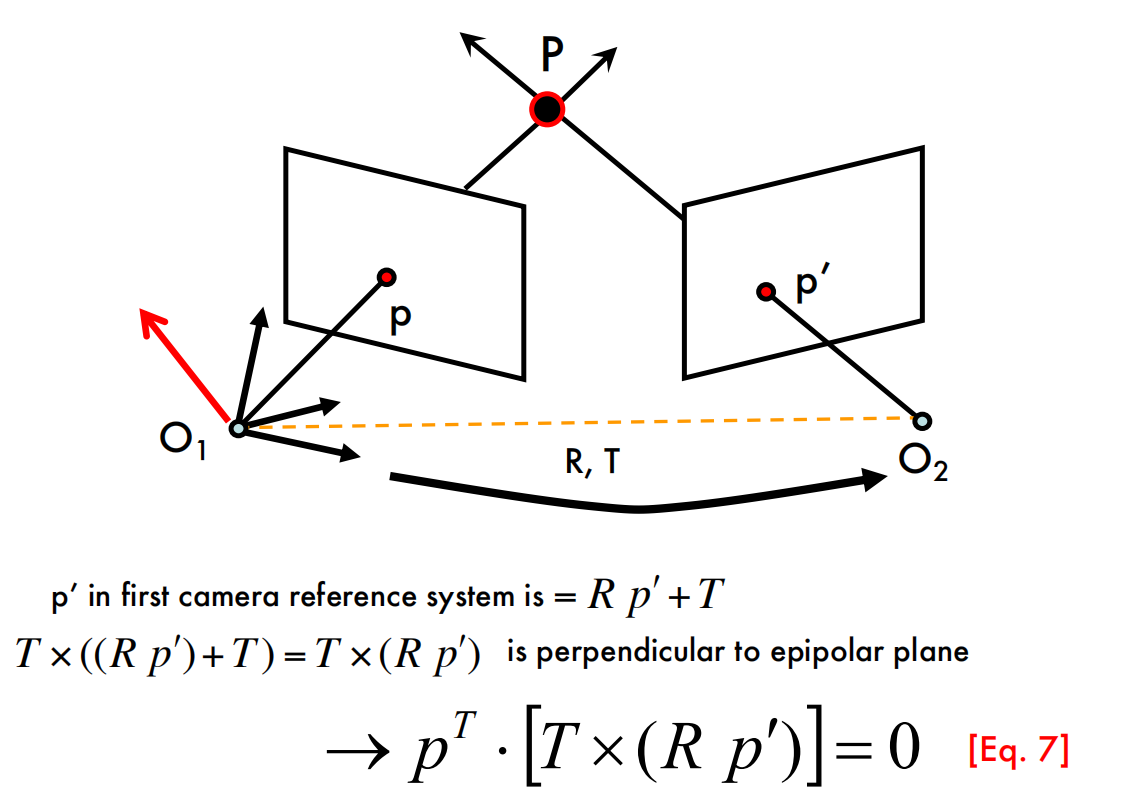
Epipolar constraints
- Two views of the same object
- Given a point on left image, how can I find the corresponding point on right image?
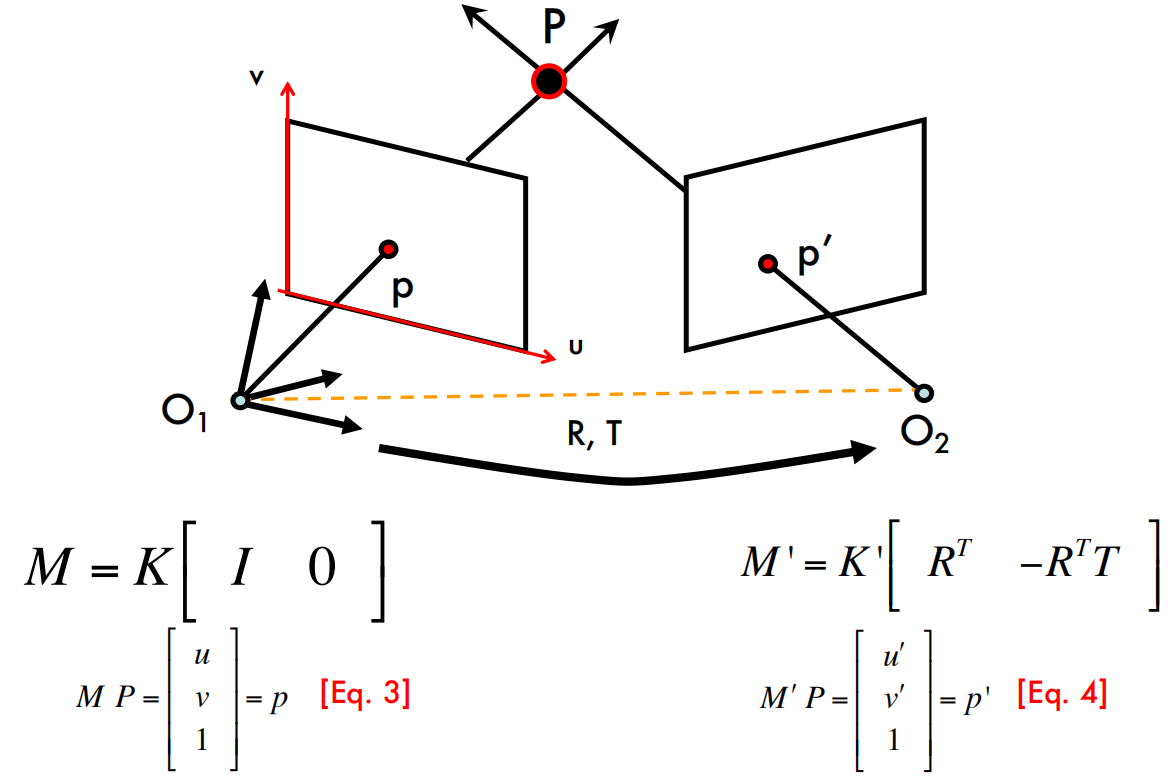
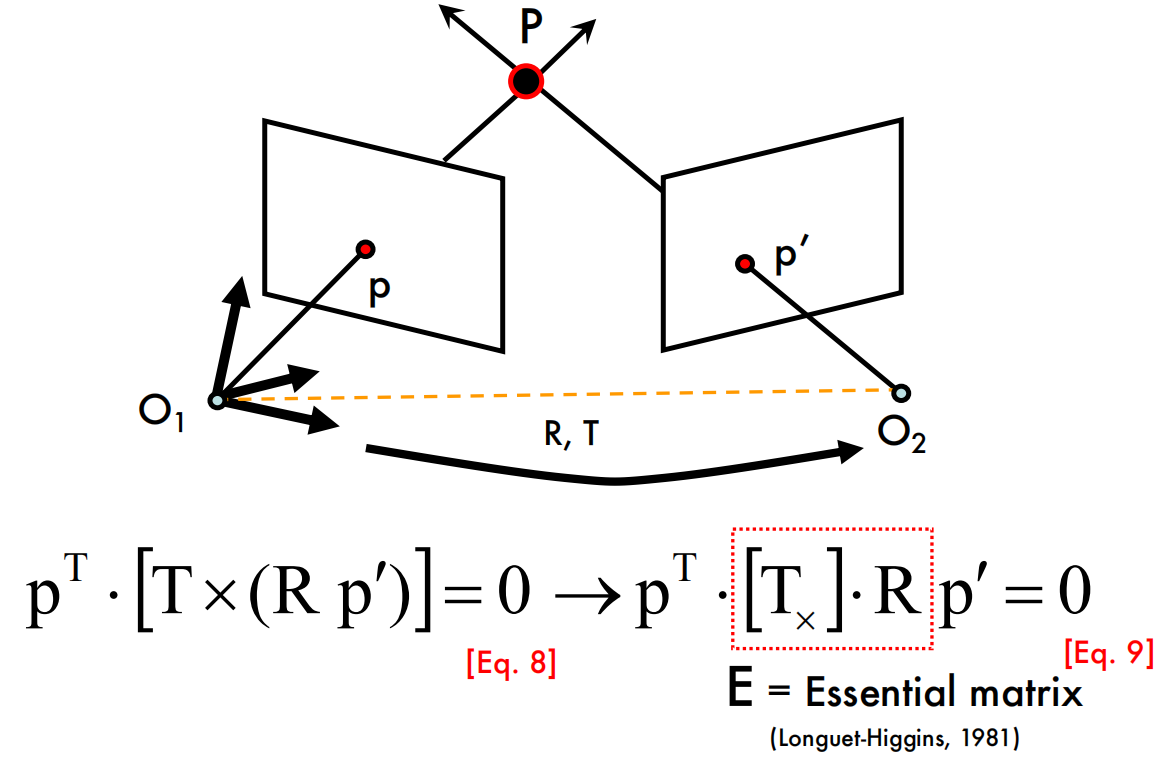
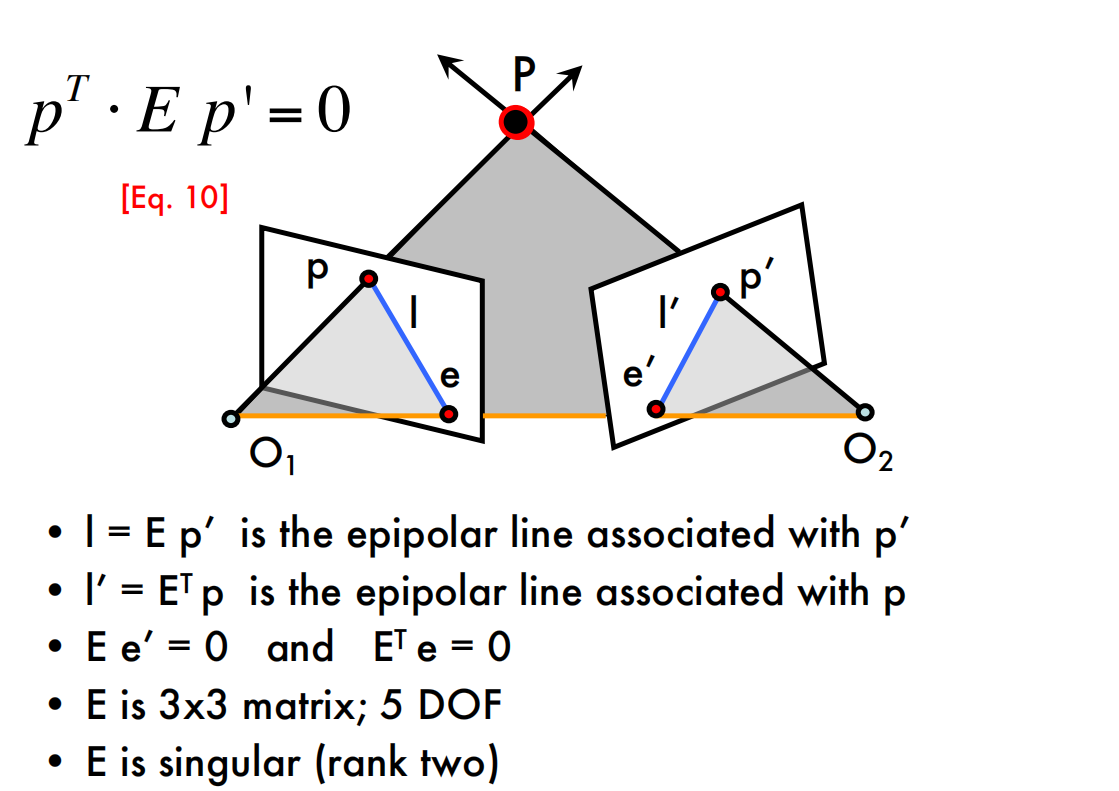
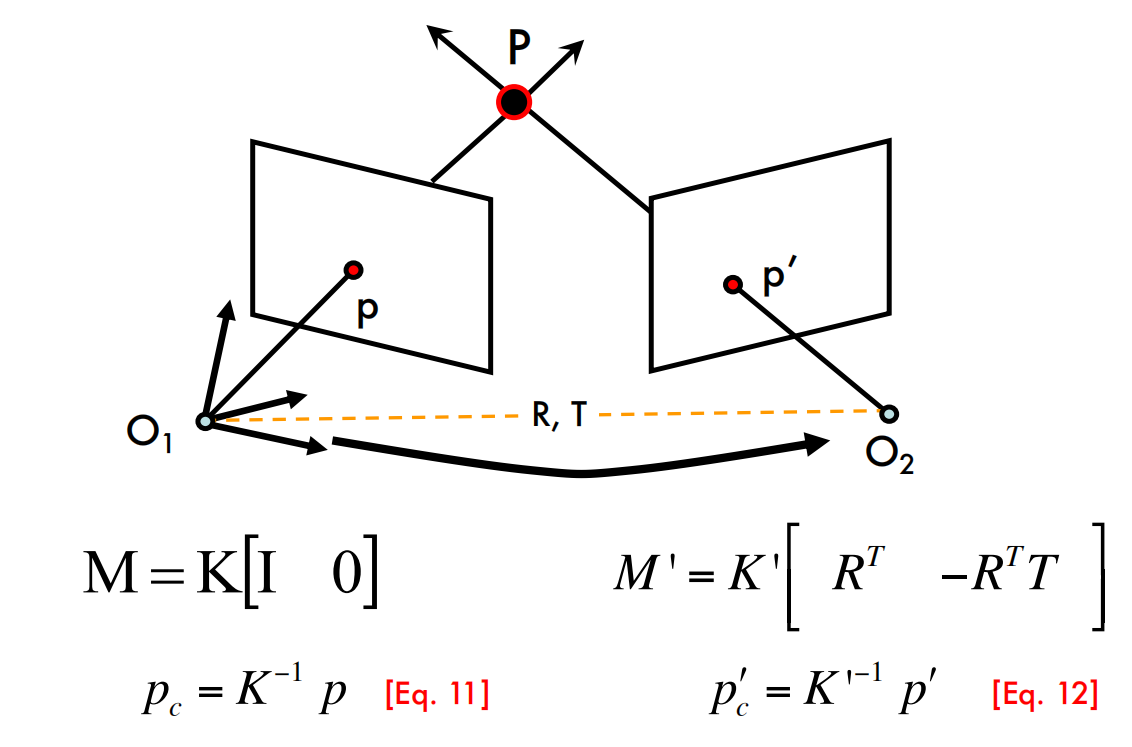
The Essential Matrix
Cross product as matrix multiplication
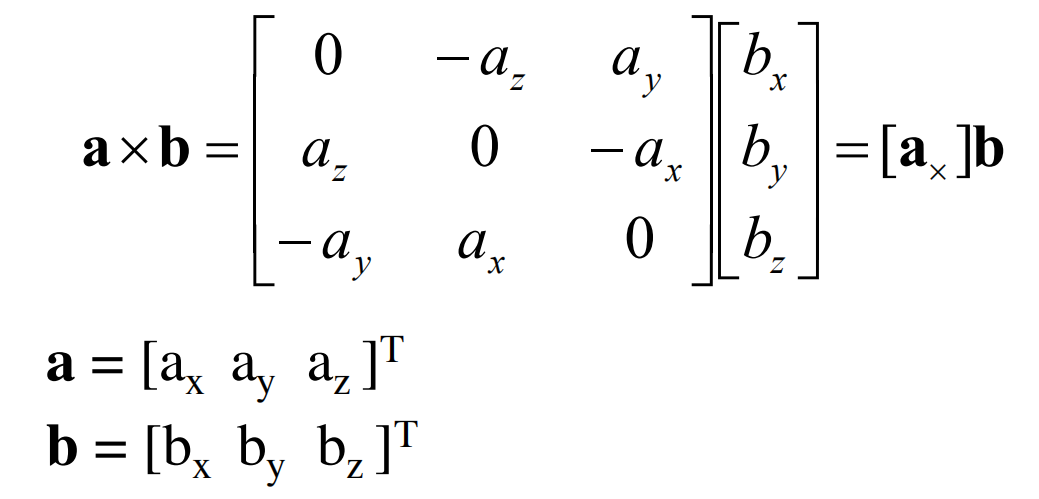
思考:
在这个部分,点$p$和$p’$都是齐次的,是像素点的归一化平面上的坐标,而不是像素点坐标;
在这种情况下,相机是标准相机,内参$K$为单位矩阵。
在《视觉SLAM十四讲》中,使用齐次坐标表示像素点是为了表达一个投影关系,这样的话$s\mathrm p$与$\mathrm p$成投影关系,它们在齐次意义下相等,也可以说在尺度意义下相等;
这样处理就可以忽略像素点$p$和$p’$的深度(回想一下相机模型),然后去构造一个和上面相同的等式(方法都是相同的,细节有点区别而已。。)
本质矩阵$E$是平移和旋转做叉乘得到的,但是由于尺度等价性,它只有5个自由度。
疑问:
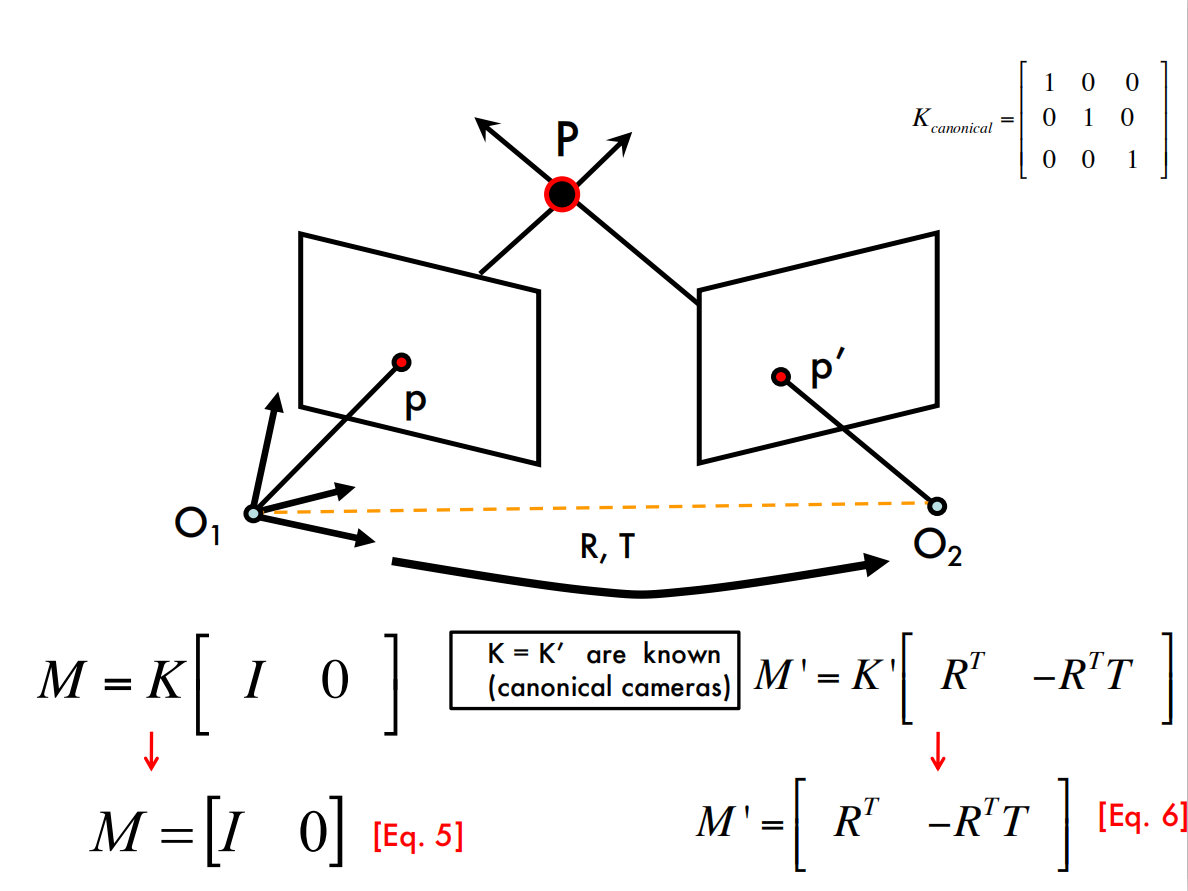
Q:什么是canonical cameras?
A:TODO(感觉是一个定义吧,内参已知的相机就可以转化为canonical camera,然后canonical camera的内参矩阵为单位矩阵)
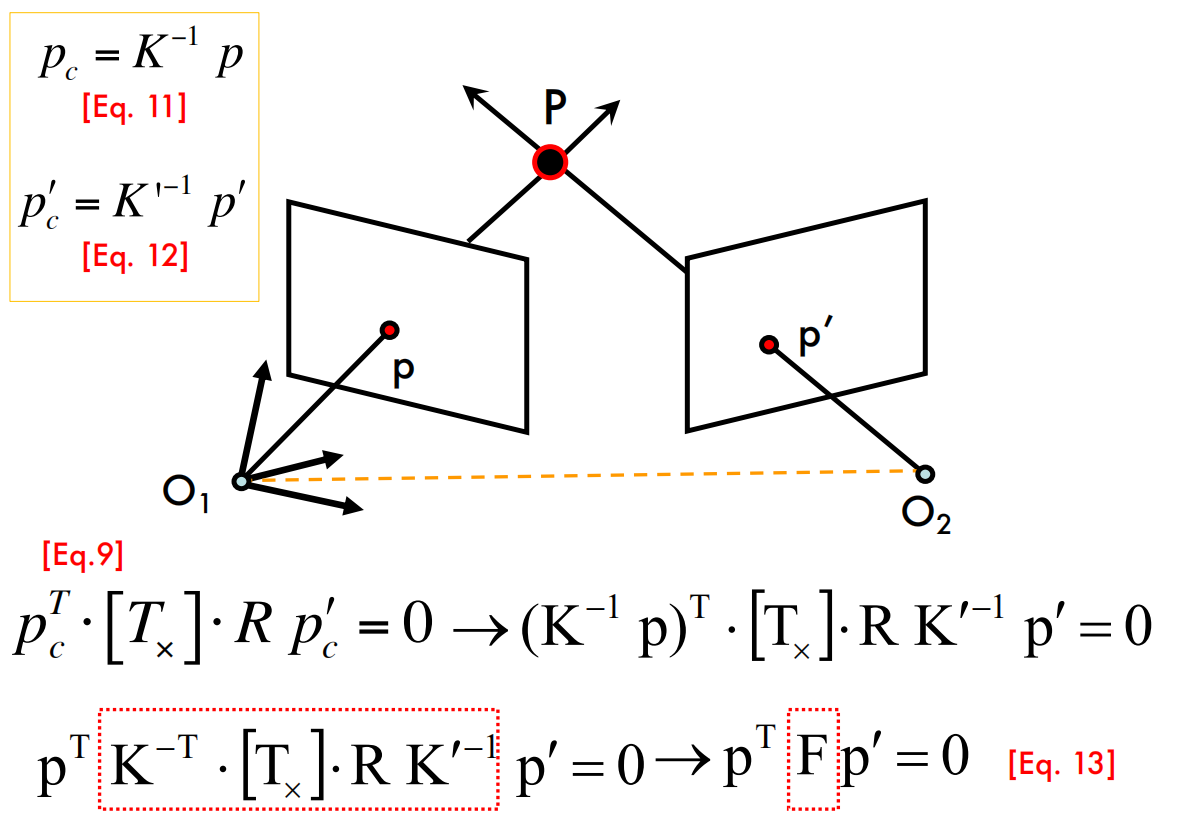
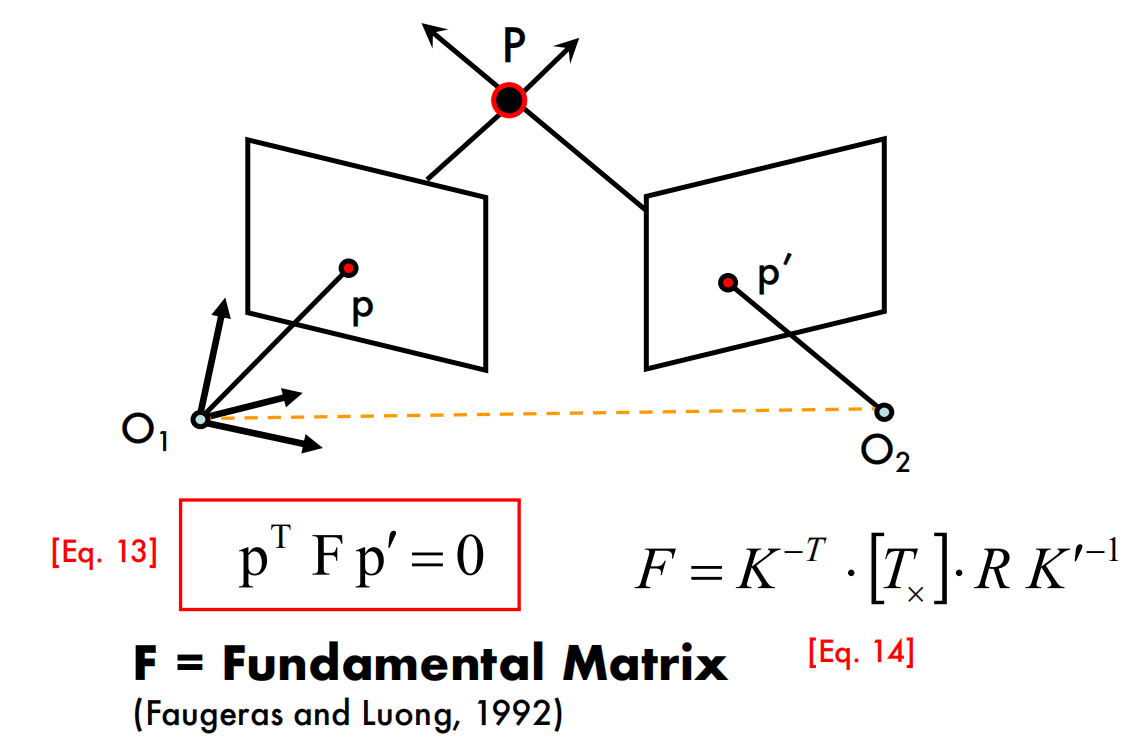
The Fundamental Matrix
思考:
- 这部分的ppt和Essential Matrix非常类似,不过这部分考虑了相机内参$K$,指出了像素点$p$与canonical camera下像素点$p_c$的对应关系。
- 在《视觉SLAM十四讲》中,是直接从像素点$p$推导到了最后的一个等式,然后把等式中间的部分记作基础矩阵$F$和本质矩阵$E$(所以讲的没这门课的清楚。。)
- 本质矩阵则是基本矩阵的一种特殊情况,是在归一化图像坐标下的基本矩阵。
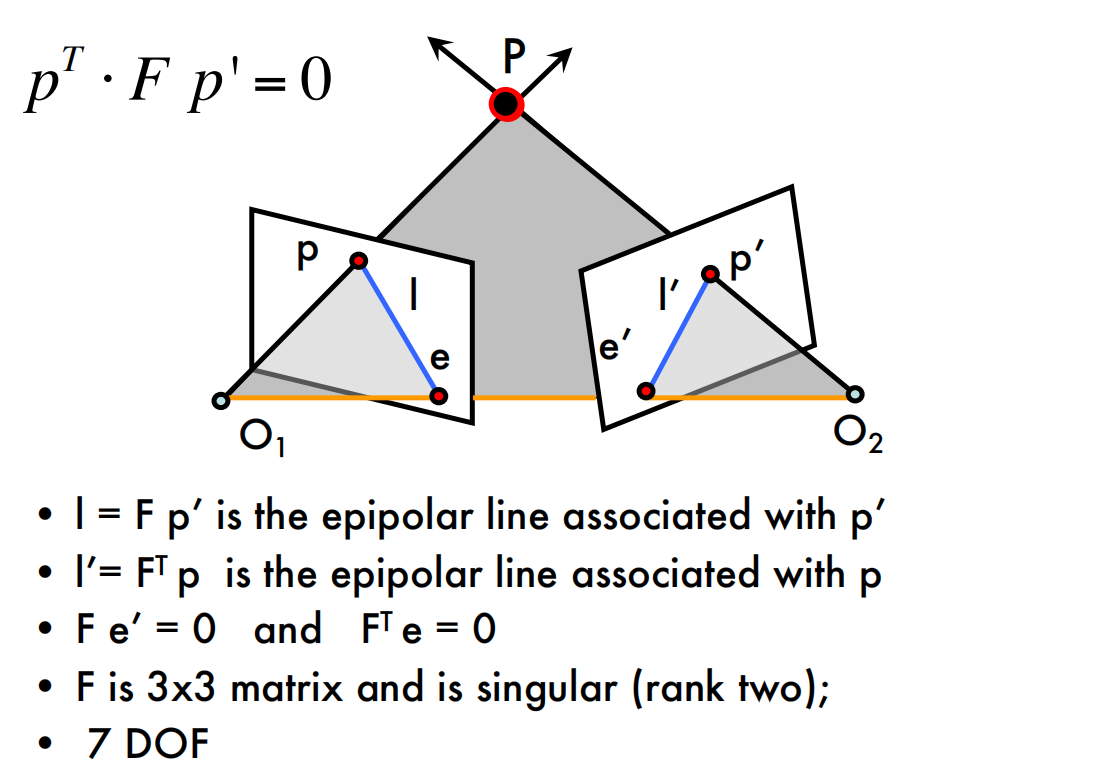
Why F is useful?
- Suppose $F$ is known
- No additional information about the scene and camera is given
- Given a point on left image, we can compute the corresponding epipolar line in the second image
- $F$ captures information about the epipolar geometry of 2 views + camera parameters
- MORE IMPORTANTLY: $F$ gives constraints on how the scene changes under view point transformation (without reconstructing the scene!)
- Powerful tool in:
- 3D reconstruction
- Multi-view object/scene matching
Estimating F
The Eight-Point Algorithm
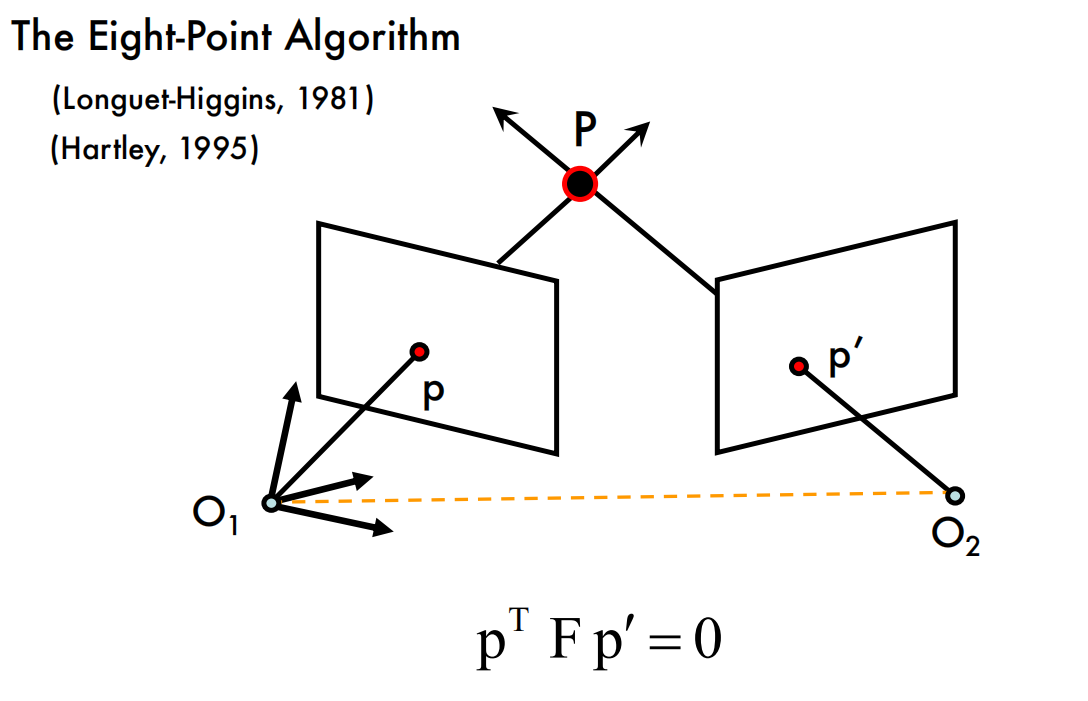




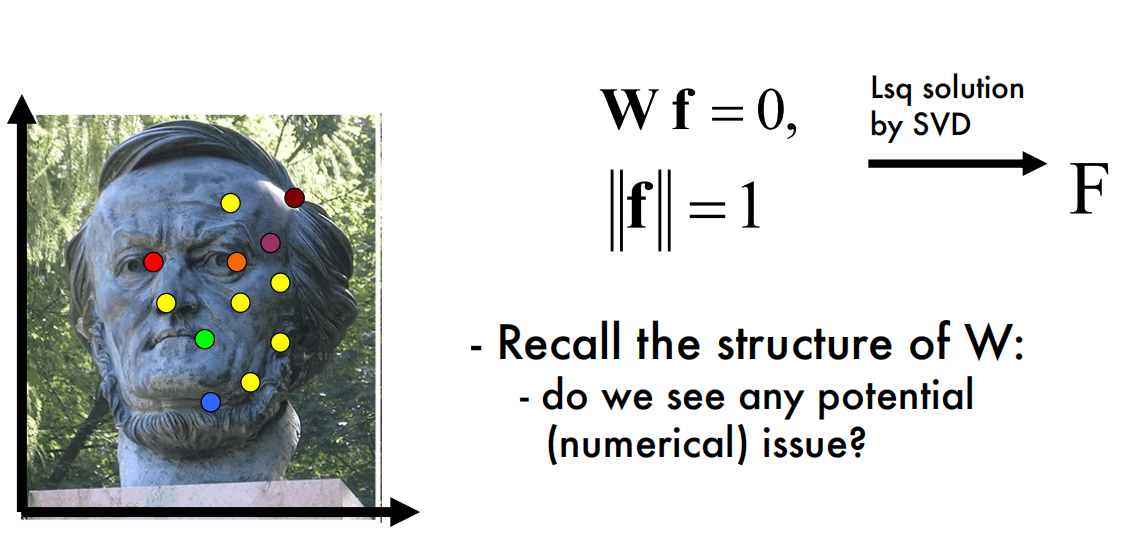
Problems with the 8-Point Algorithm

思考:
在《视觉SLAM十四讲》中,主要介绍了八点法求解本质矩阵$E$。
与上面不同的是,本质矩阵$E$的$\Sigma=diag(\sigma,\sigma,0)$,而基础矩阵$F$的$\Sigma=diag(s_1,s_2,0)$。
The Normalized Eight-Point Algorithm
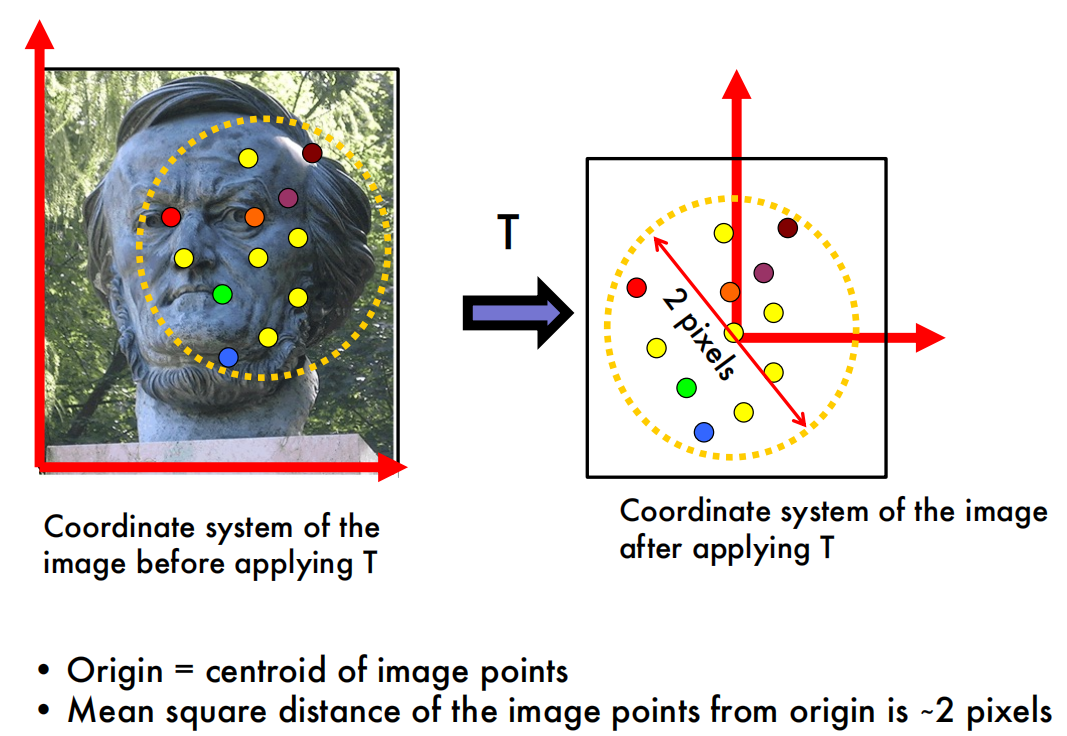
Normalization

Example of normalization
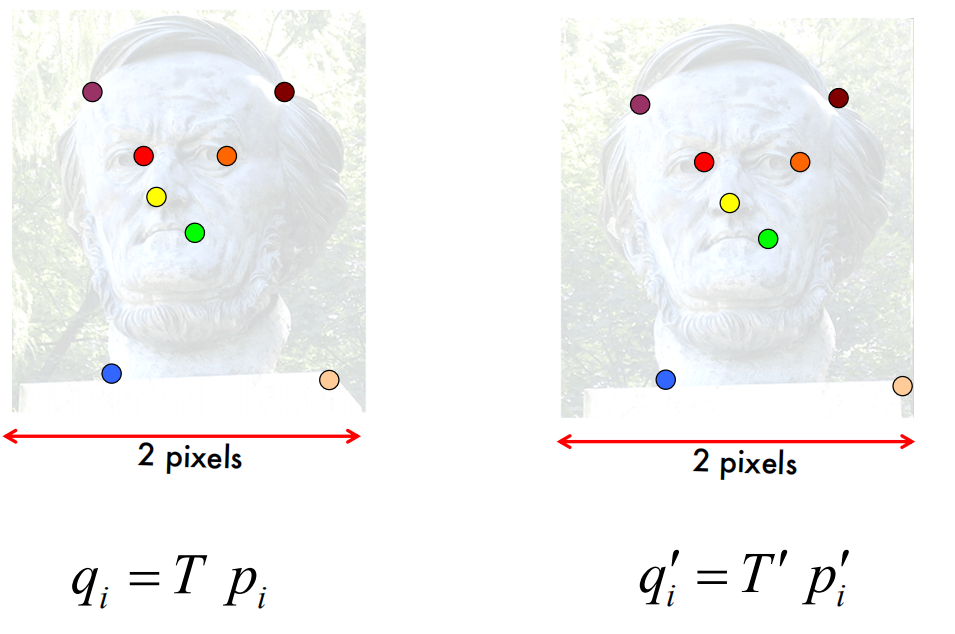
The Normalized Eight-Point Algorithm

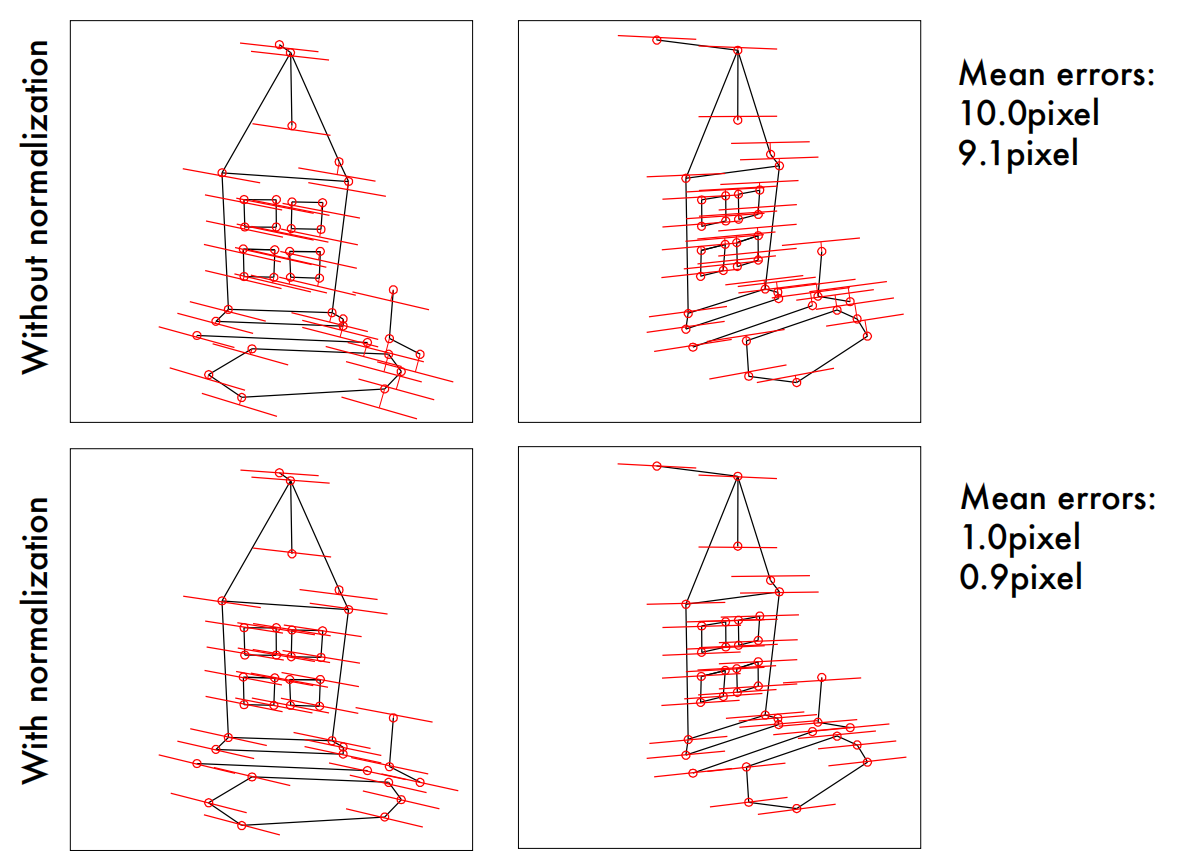
思考:
这里的normalize就是用另外的图像坐标系表示匹配的特征点,让特征点更均匀的散布在坐标原点周围。如果特征点散布在同一块地区,彼此非常接近,或者有的特征点的数值非常大,可能会对矩阵$W$带来不好的影响。
由于更改了图像的坐标系,这里计算出来的基础矩阵$F$还需要再de-normalize一下。
在course notes 3上有更详细的解读:
The main problem of the standard Eight-Point Algorithm stems from the fact that $W$ is ill-conditioned for SVD. For SVD to work properly, $W$ should have one singular value equal to (or near) zero, with the other singular values being nonzero. However, the correspondences $p_i = (u_i, v_i, 1)$ will often have extremely large values in the first and second coordinates due to the pixel range of a modern camera (i.e. $p_i = (1832, 1023, 1)$). If the image points used to construct $W$ are in a relatively small region of the image, then each of the vectors for $p_i$ and $p′_i$ will generally be very similar. Consequently, the constructed $W$ matrix will have one very large singular value, with the rest relatively small.
To solve this problem, we will normalize the points in the image before constructing $W$. This means we pre-condition $W$ by applying both a translation and scaling on the image coordinates.



