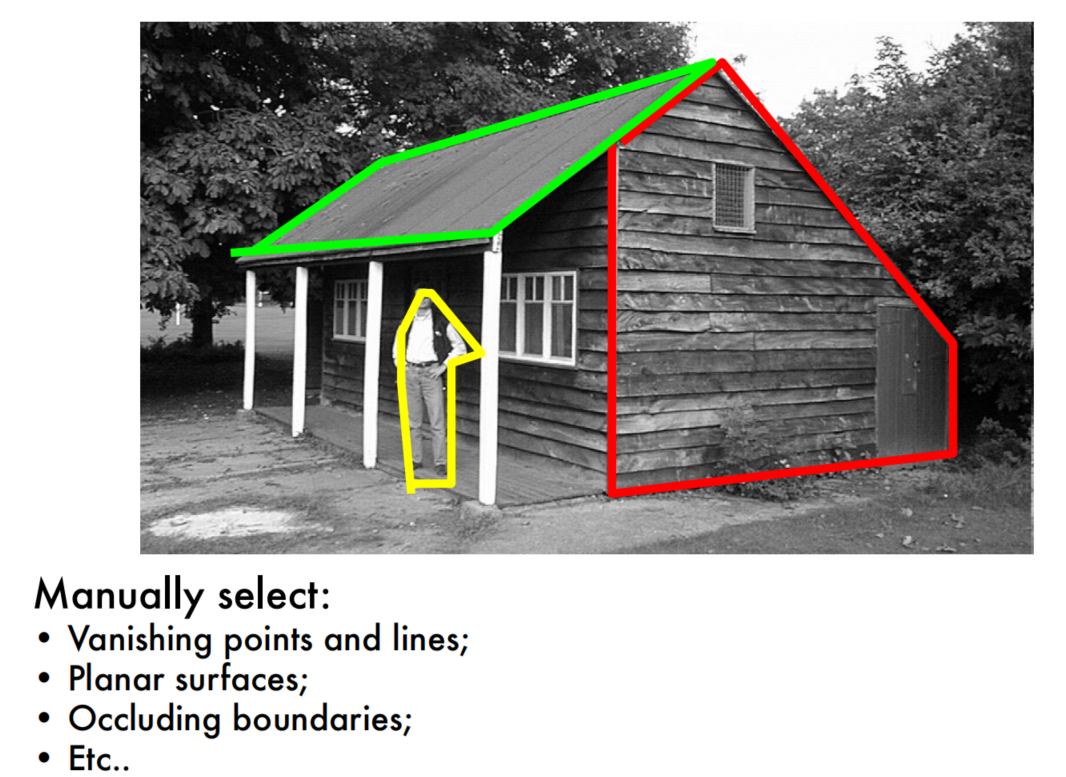
CS231A Lecture 4:Single View Metrology
Reading:
[HZ] Chapter 2 “Projective Geometry and Transformation in 2D”
[HZ] Chapter 3 “Projective Geometry and Transformation in 3D”
[HZ] Chapter 8 “More Single View Geometry”
[Hoeim & Savarese] Chapter 2
2D transformations
这部分介绍了四种2D变换:Isometries、Similarities、Affinity、Projective
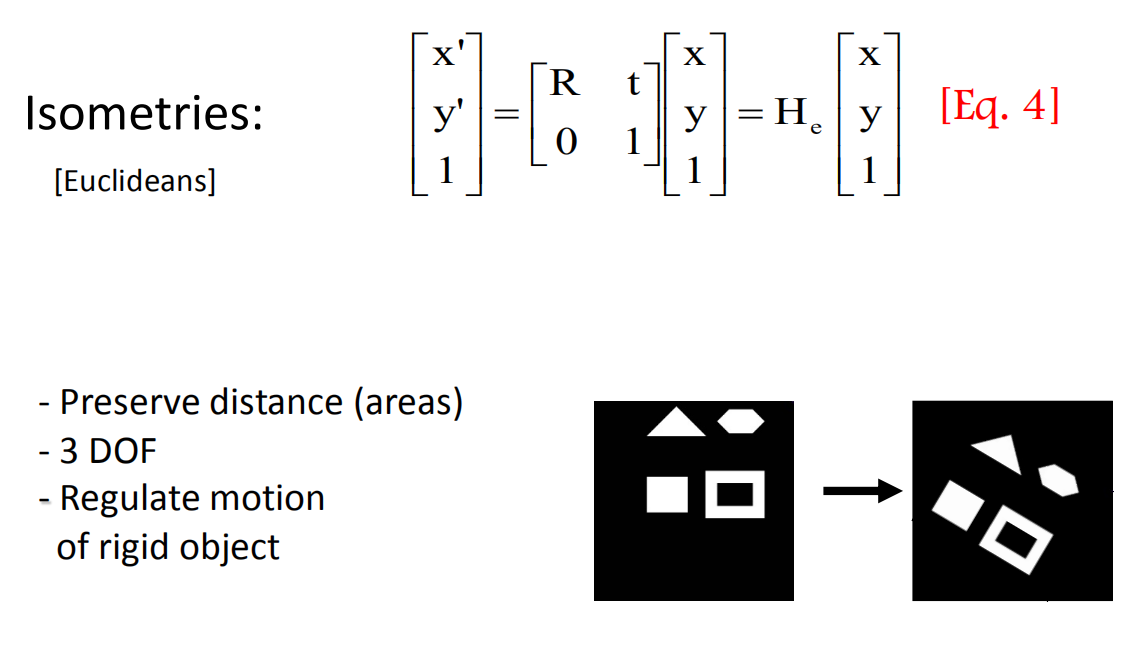
Isometries
等距变换(Isometries),旋转+平移。
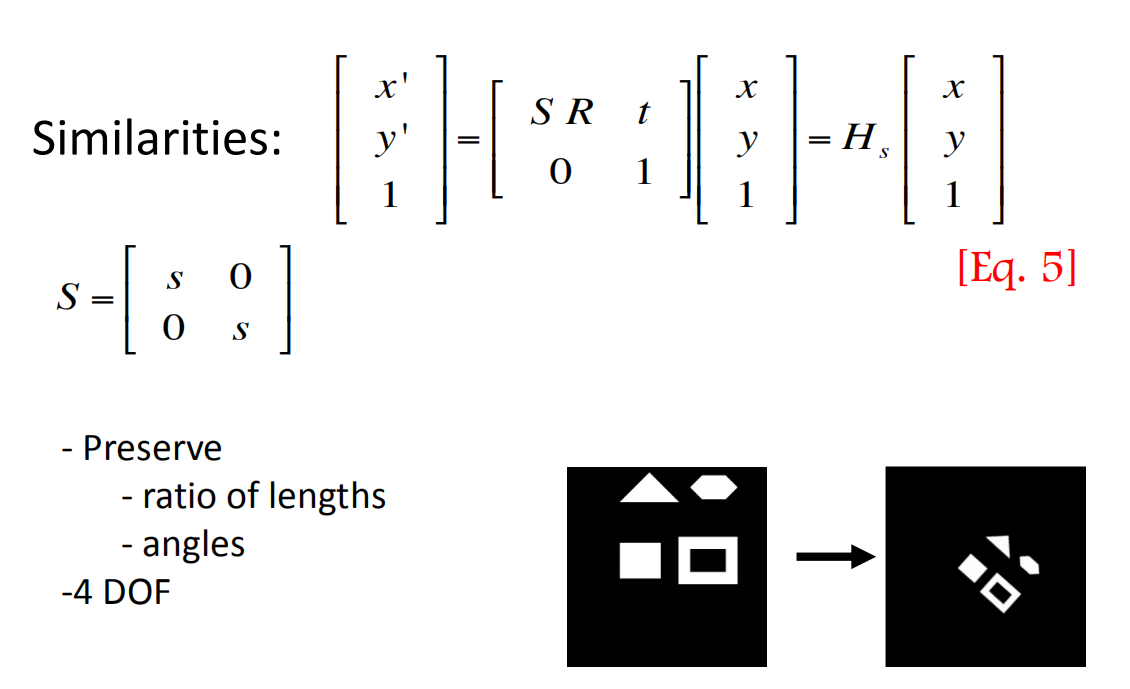
Similarities
相似变换(Similarities),相当于是等距变换与均匀缩放的结合。
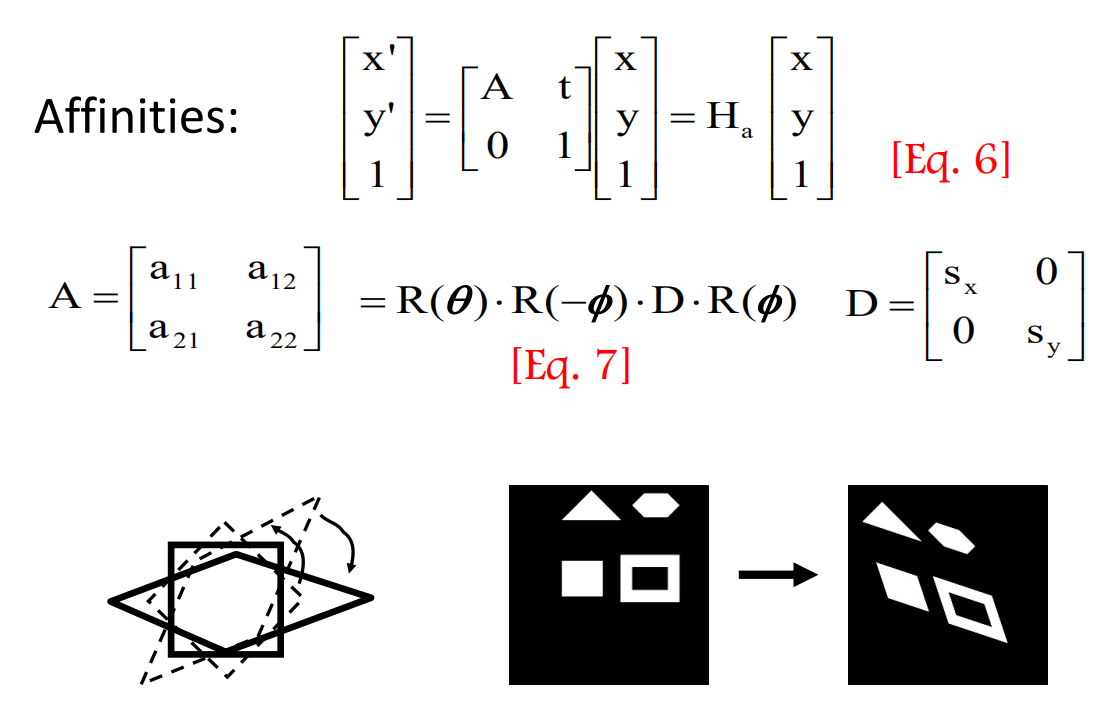
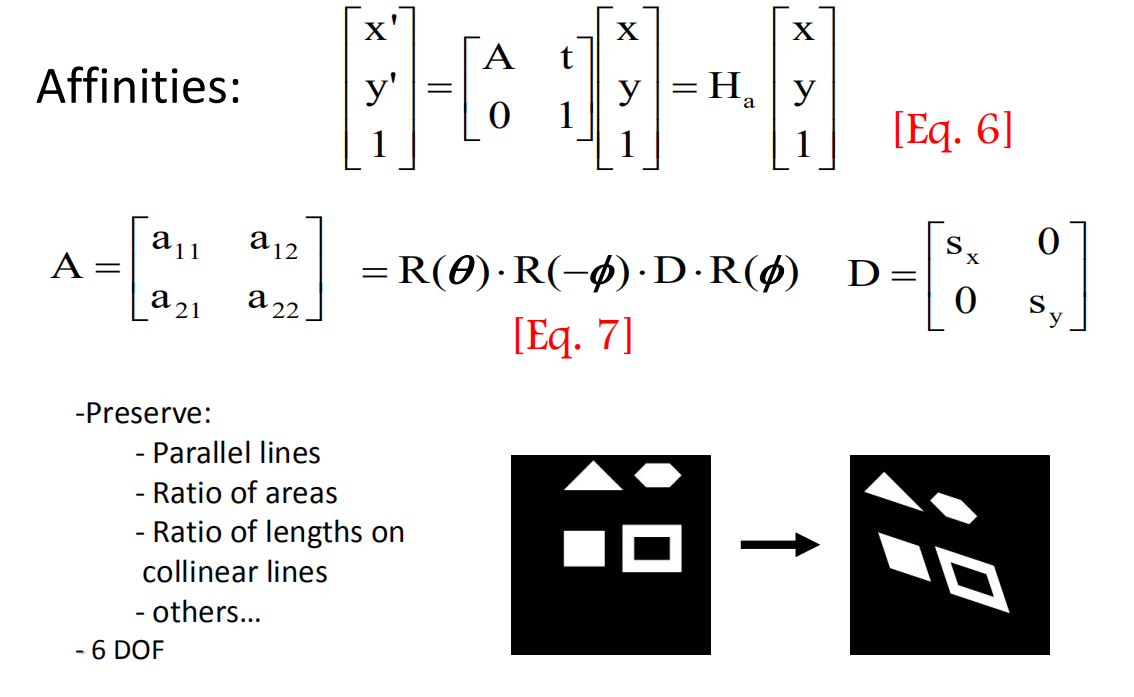
Affinity
仿射变换(Affine),是一个平移变换与一个非奇异线性变换的结合。
其中的A矩阵可以理解成旋转与非均匀缩放的结合。
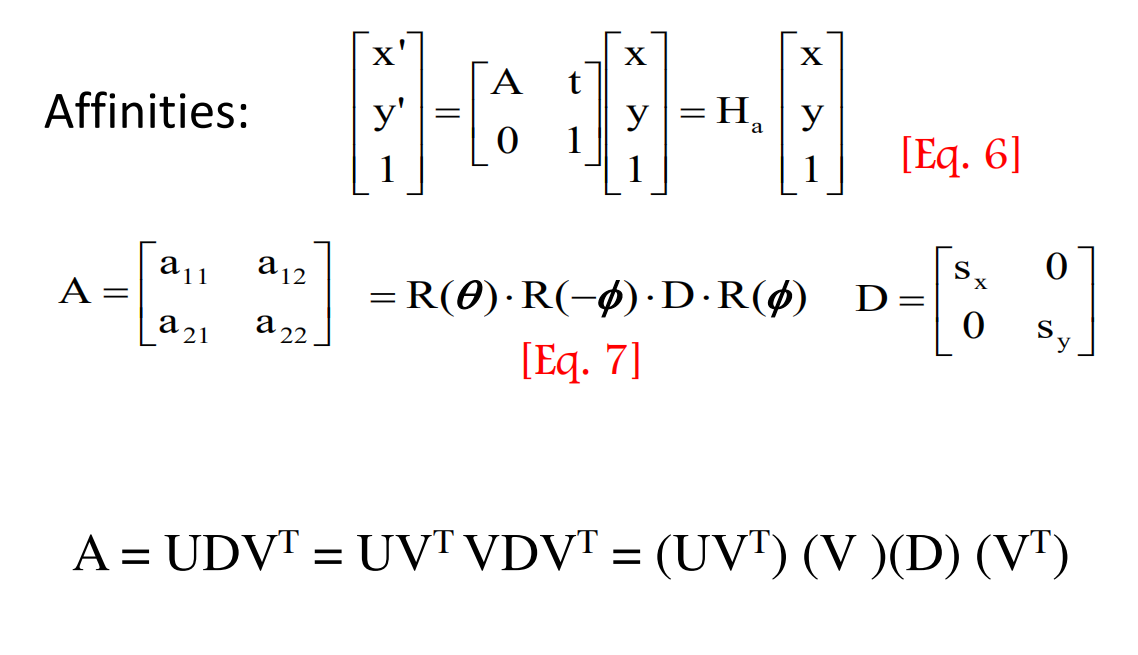
Projective
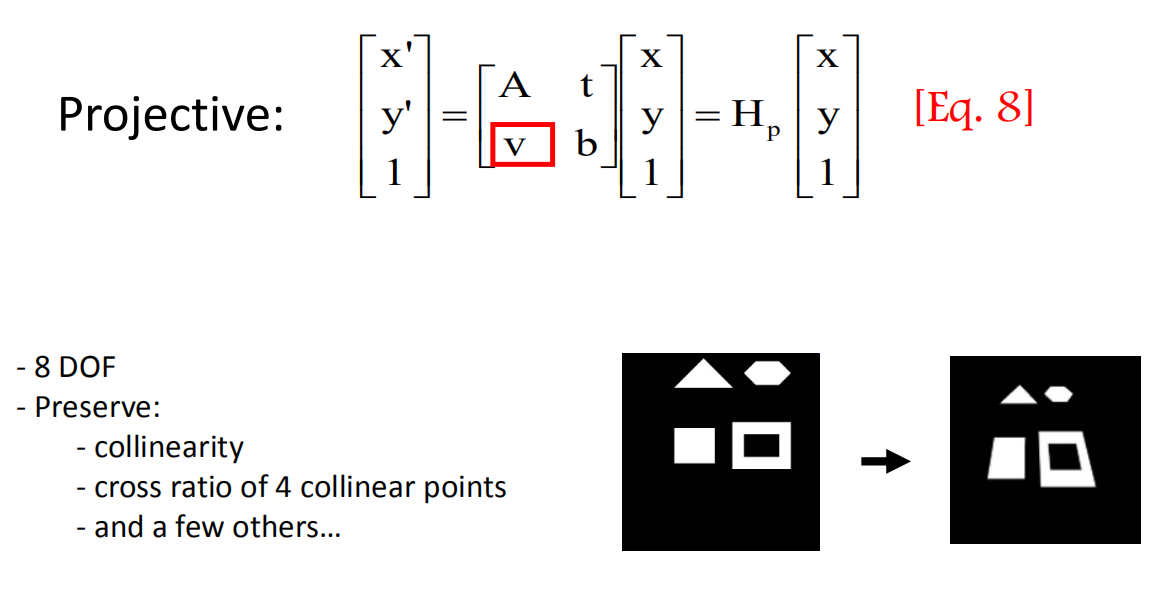
射影变换(Projective),是齐次坐标的一般非奇异线性变换,扩展了仿射变换,是非齐次坐标的一般非奇异线性变换和一个平移的复合。
定义:由有限次中心射影的积定义的两条直线间的一一对应变换称为一维射影变换。由有限次中心射影的积定义的两个平面之间的一一对应变换称为二维射影变换。
性质:交比不变性
如果平面上点场的点建立了一个一一对应,并且满足:
(1)任何共线三点的象仍是共线三点;
(2)共线四点的交比不变。
则这个一一对应叫做点场的射影变换,简称射影变换。
The cross ratio:
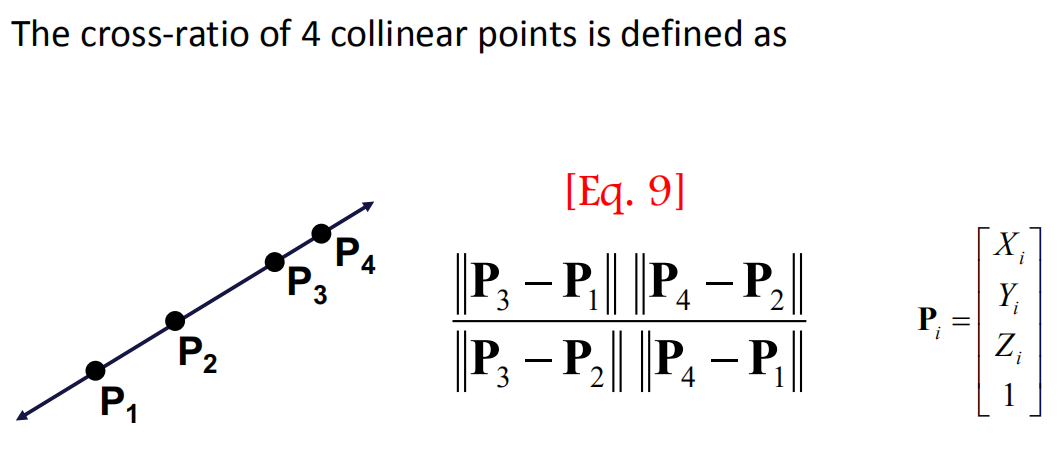
与其他变换的关系:
$H$矩阵是可逆实矩阵,当$v$等于0则变成了仿射变换;在仿射变换的前提下,左上角的$2 \times 2$矩阵正交时为相似变换;左上角矩阵行列式为1时为等距变换。
射影变换可以分解成一串交换链的复合。
$$
H = H_{S}H_{A}H_{P} =
\begin{bmatrix} sR&t \\ 0^{T} & 1 \end{bmatrix}
\begin{bmatrix} K&0 \\ 0^{T} & 1 \end{bmatrix}
\begin{bmatrix} I&0 \\ V^{T} & v \end{bmatrix} =
\begin{bmatrix} A & Vt\\ V^{T} & v \end{bmatrix}
$$
可以看出上式中,$H_S$表示相似变换,$H_A$表示仿射变换,$H_P$表示射影变换。
Questions
Q:射影变换与仿射变换的根本区别在于射影变换中向量$v$不为0,如何理解?
A:对于理想点$(x_{1},x_{2},0)^{T}$在仿射变换与射影变换下面的映射:
在仿射变换下:
$$
\begin{bmatrix} A &t \\ 0^{T} & 1 \end{bmatrix}
\begin{pmatrix} x_{1}\\ x_{2}\\ 0 \end{pmatrix} =
\begin{pmatrix} A\begin{pmatrix} x_{1}\\ x_{2} \end{pmatrix} \\ 0 \end{pmatrix}
$$在射影变换下:
$$
\begin{bmatrix} A &t \\ V^{T} & v \end{bmatrix}
\begin{pmatrix} x_{1}\\ x_{2}\\ 0 \end{pmatrix} =
\begin{pmatrix} A\begin{pmatrix} x_{1}\\ x_{2} \end{pmatrix} \\ v_{1}x_{1}+v_{2}x_{2}
\end{pmatrix}
$$
可以看出,对于仿射变换,理想点变换后还是理想点;对于射影变换,理想点被映射到有限点。说明射影变换能对消影点建模。
Vanishing points and lines
Lines in a 2D plane
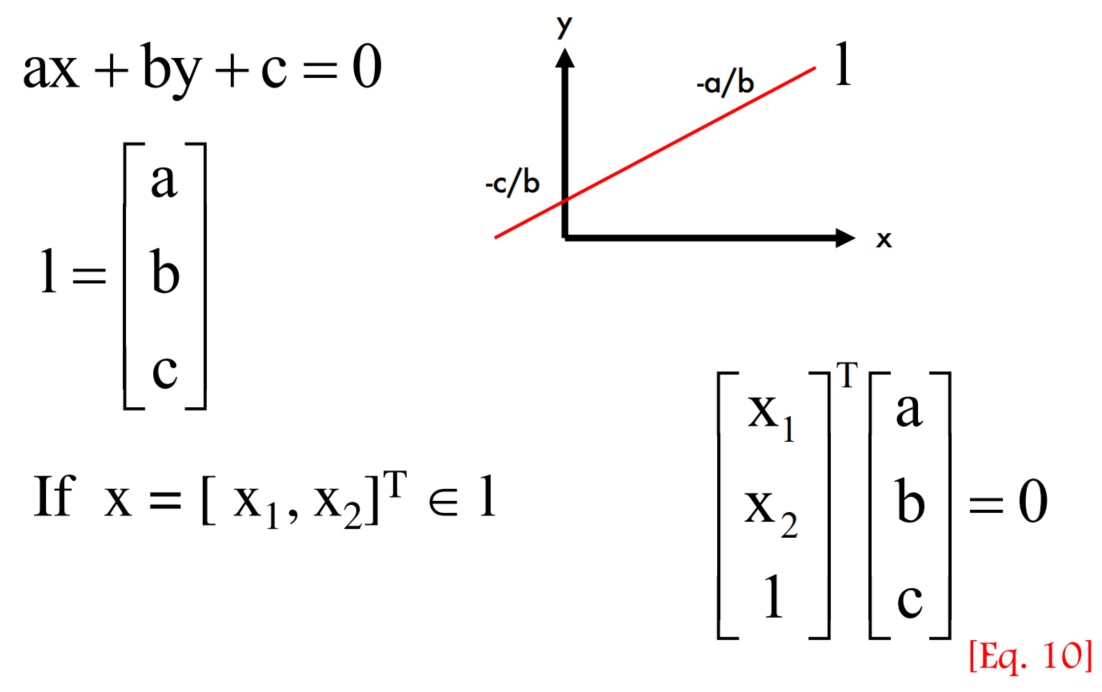
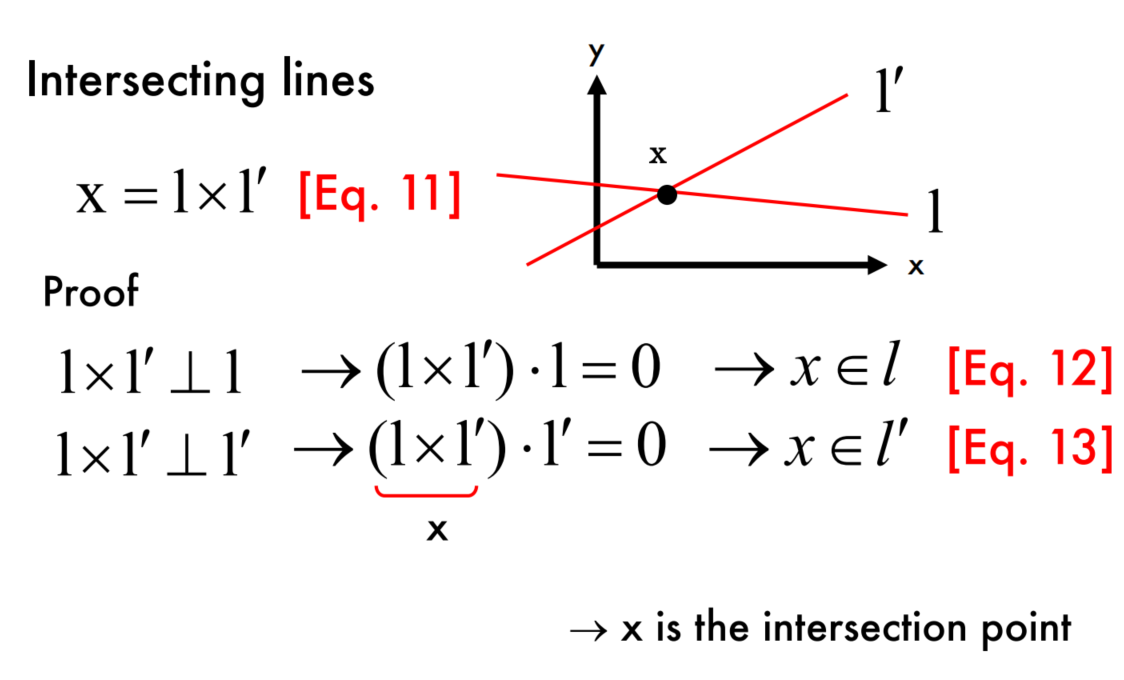
Intersecting lines
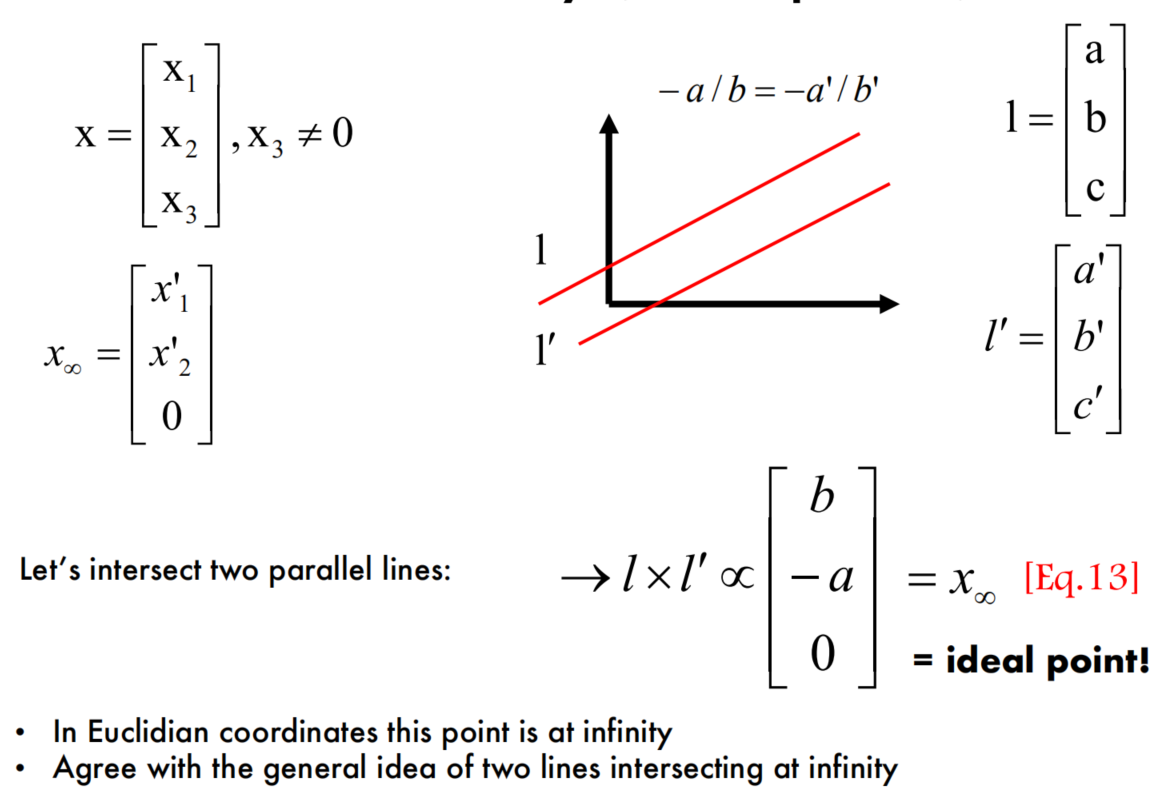
2D Points at infinity (ideal points)
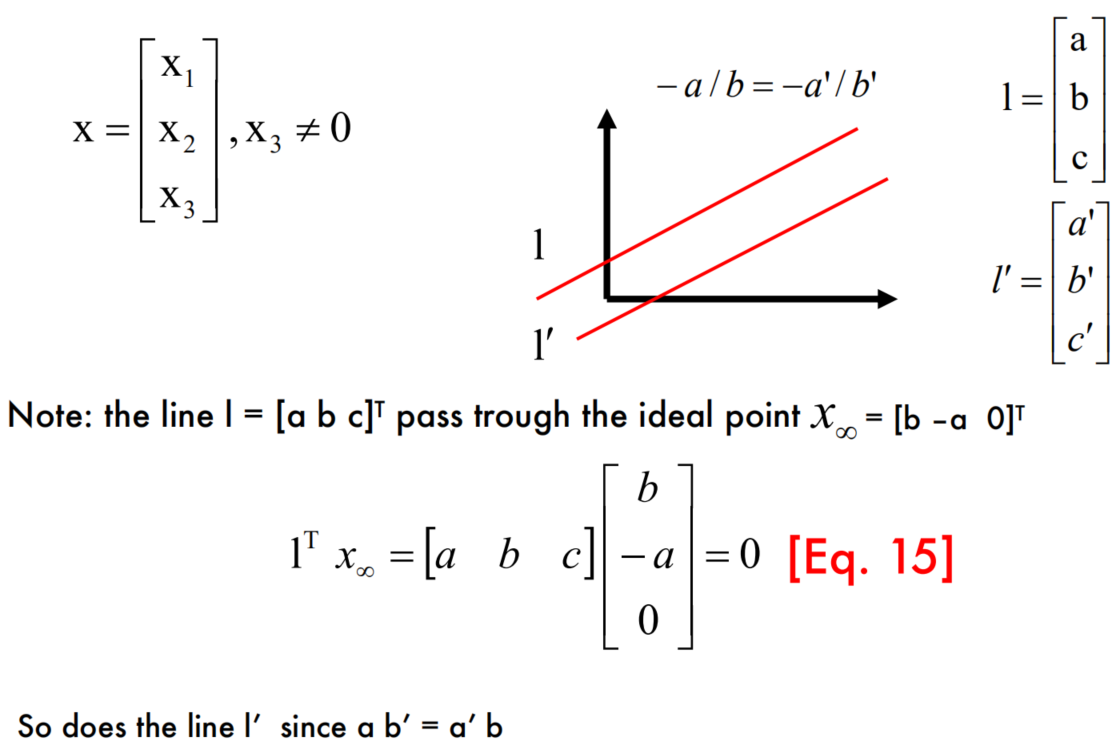
Lines infinity $l_\infty$
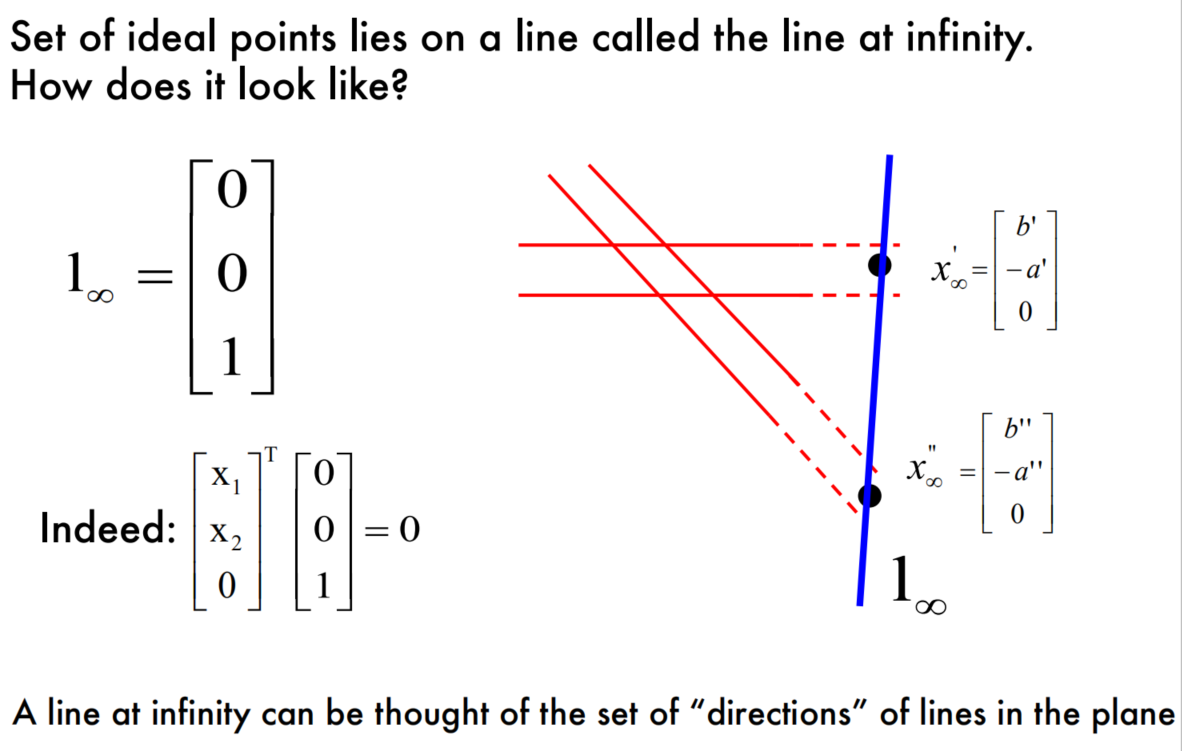
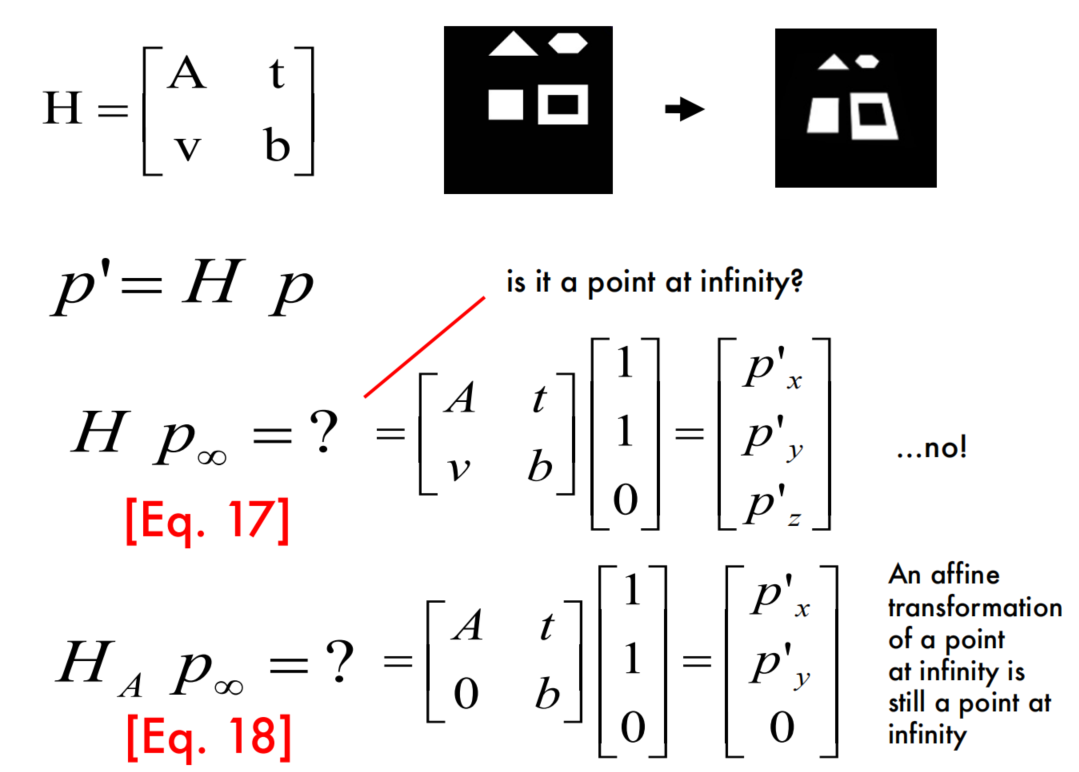
Projective transformation
这部分和2D transformations-Questions是对应的。
a point at infinity
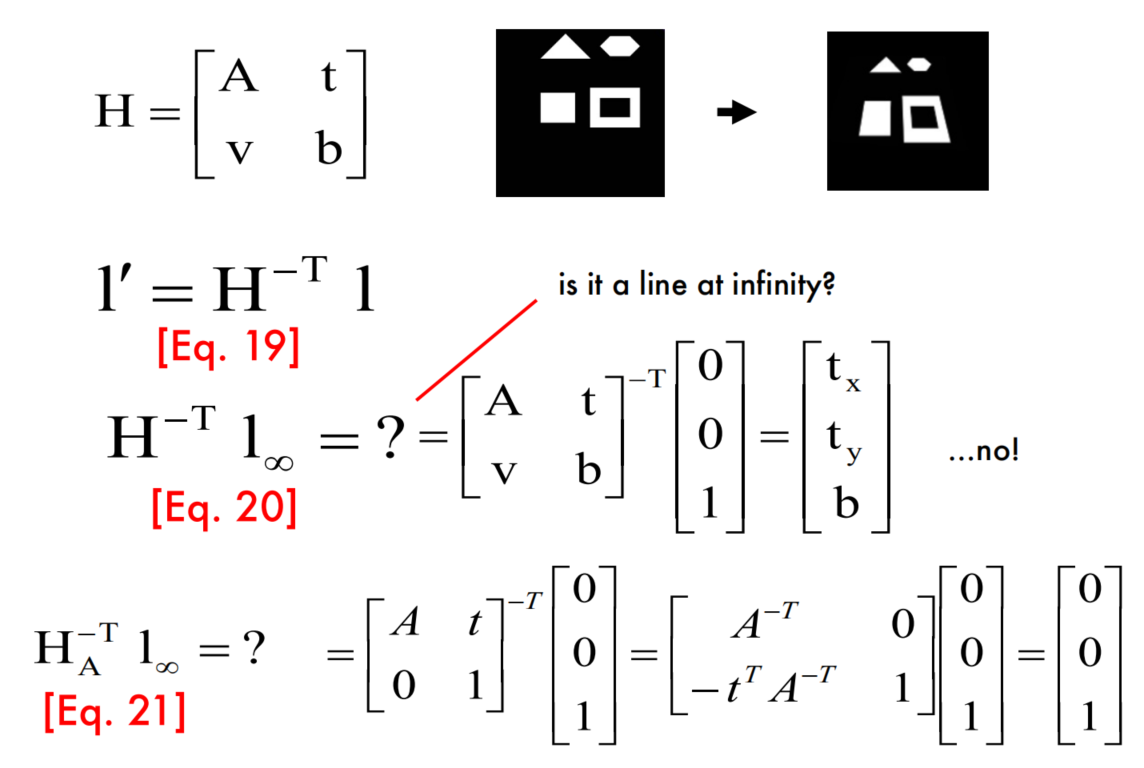
a line (in 2D)
Points and planes in 3D
3D空间中的点与平面:
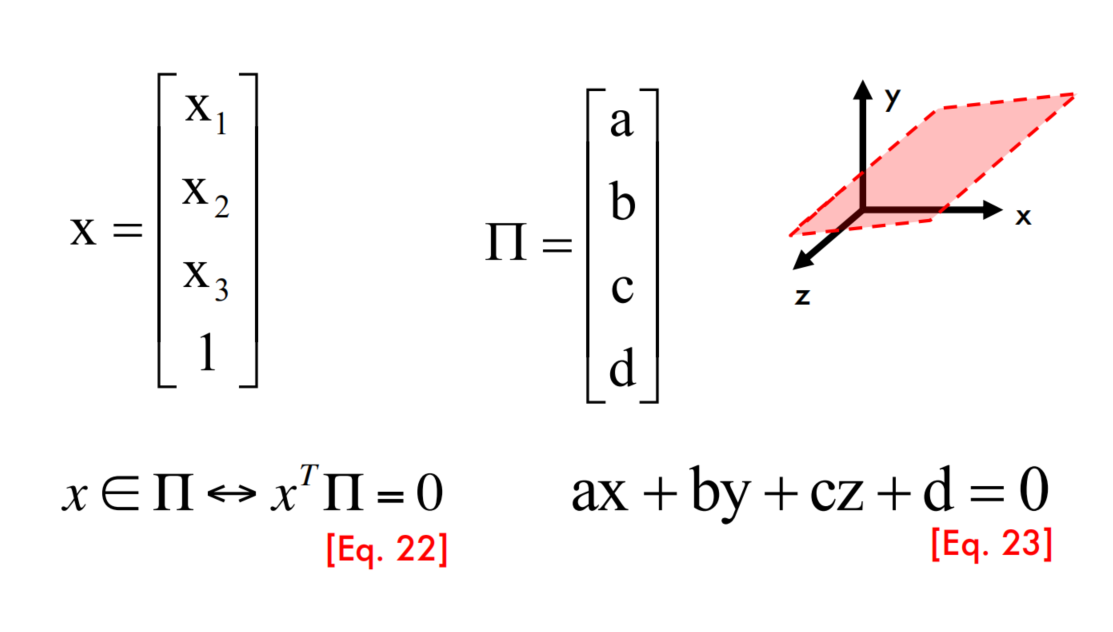
3D空间中的直线:


Points at infinity in 3D
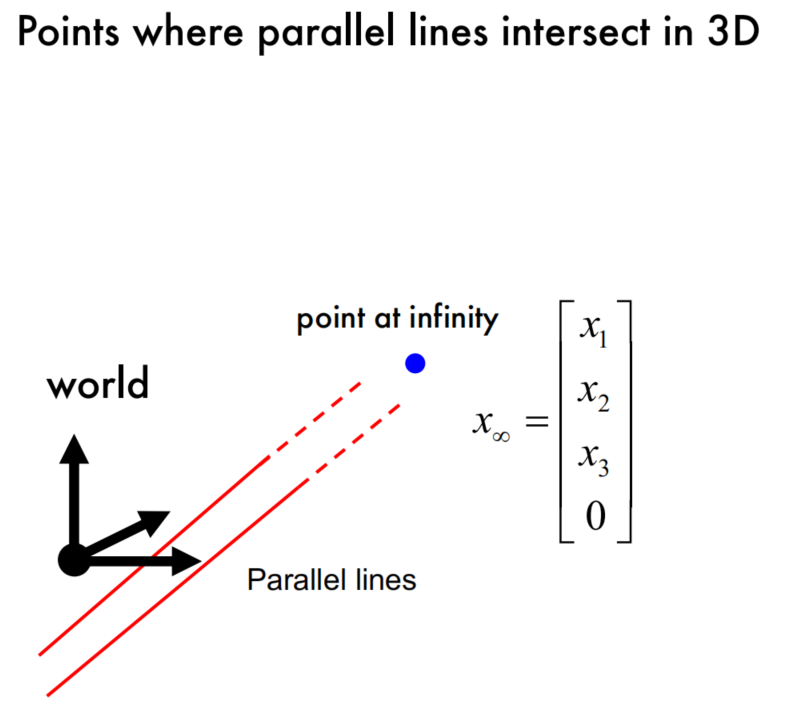
Vanishing points
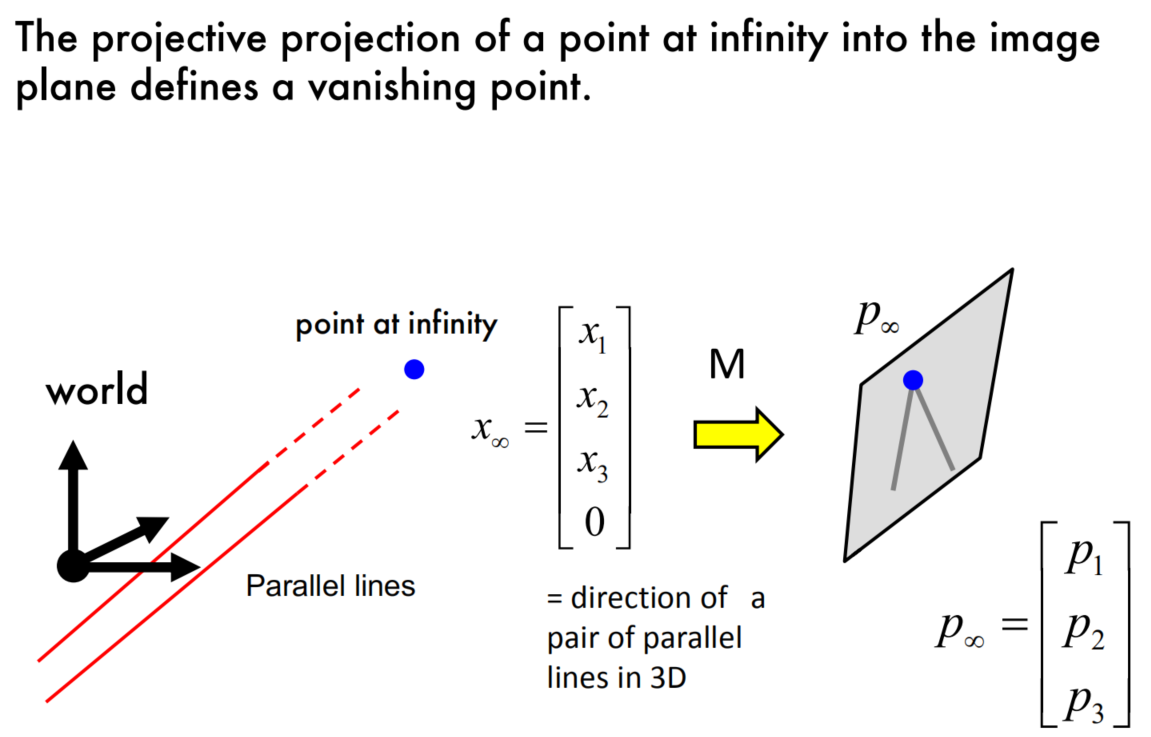
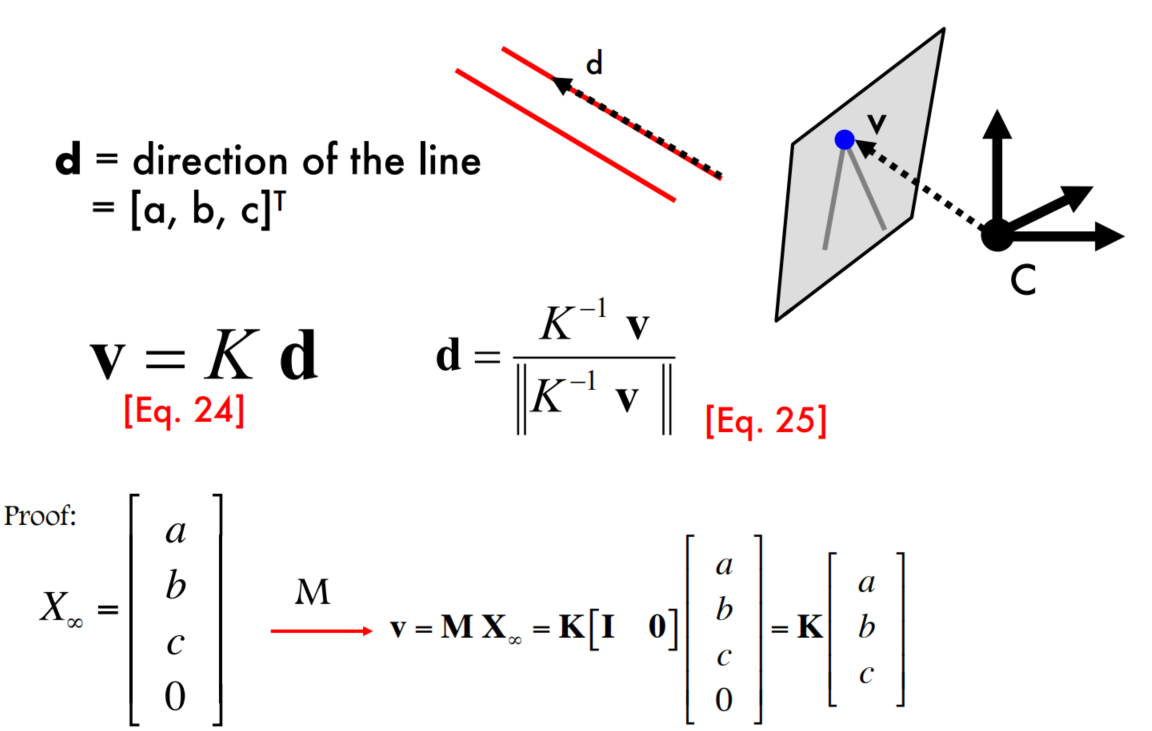
Vanishing points and directions
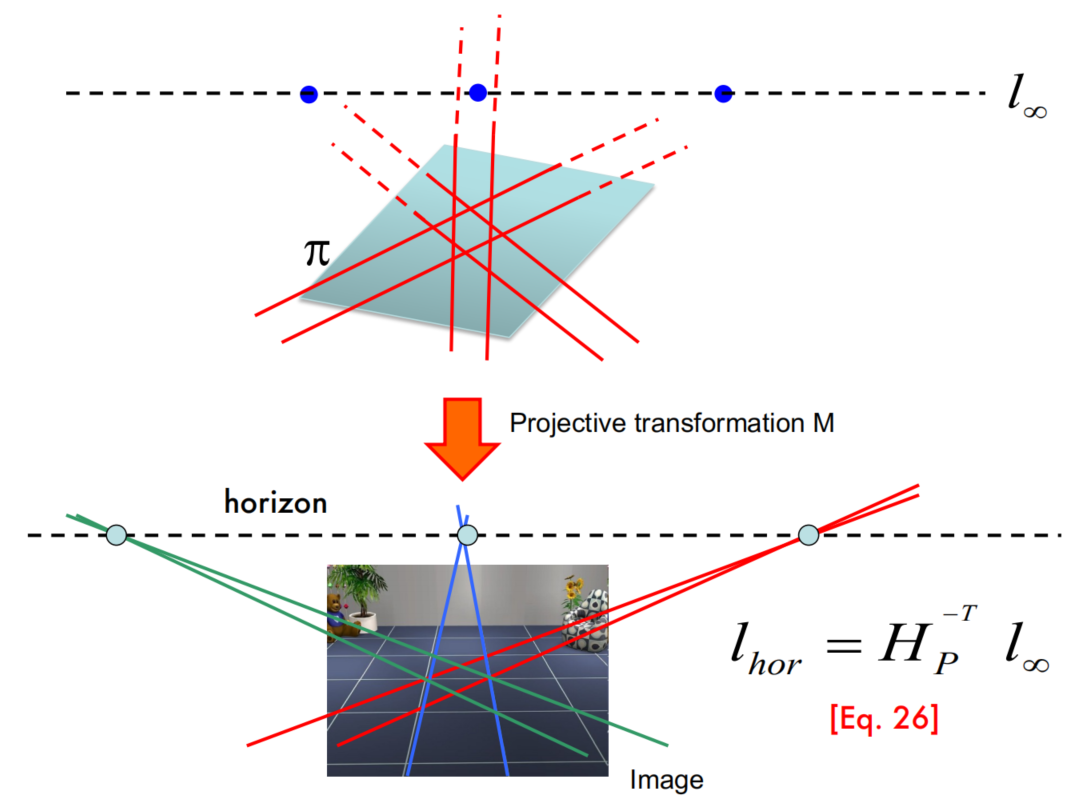
Vanishing (horizon) line
Example: Are these two lines parallel or not?

Vanishing points and planes
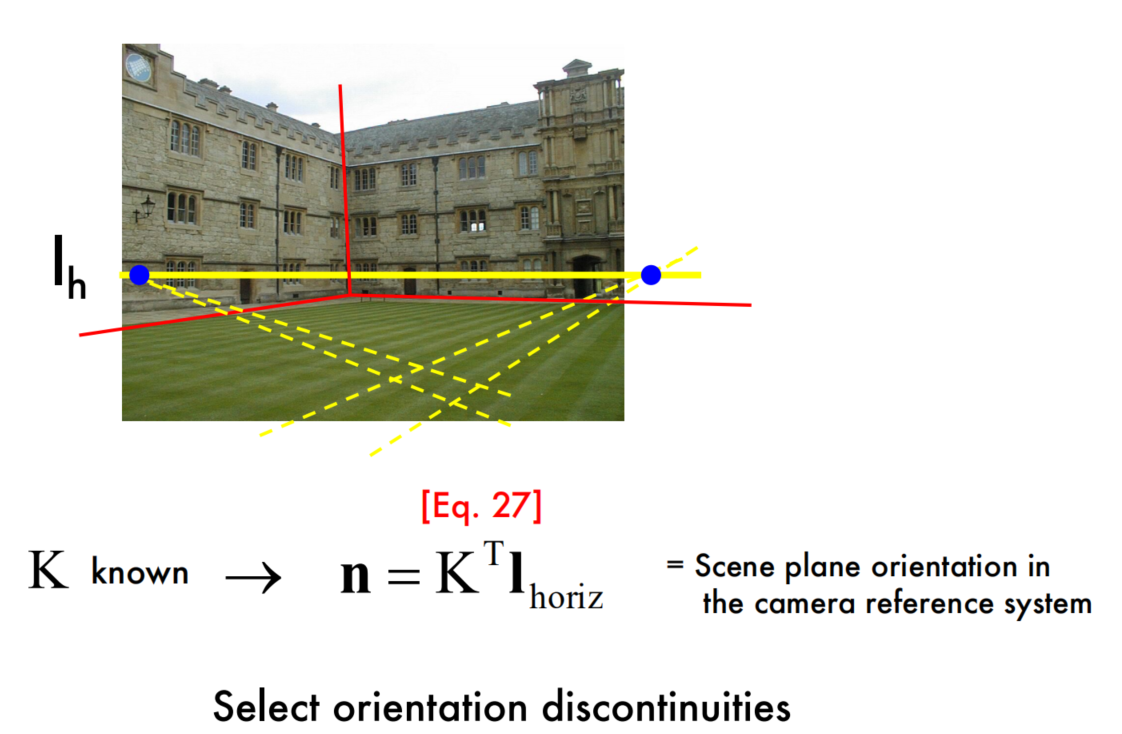
Furthermore, the horizon line allows us to compute useful properties about the world. For example, we can derive an interesting relationship between the the normal n of a plane in 3D with the corresponding horizon line $l_{horiz}$ in an image:
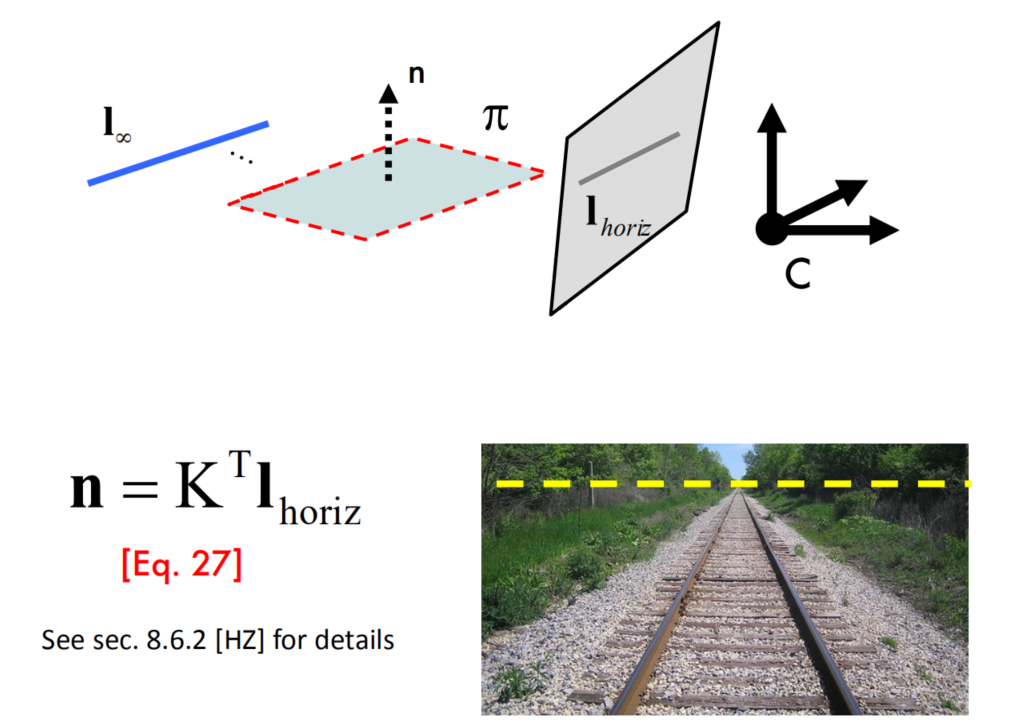
This means that if we can recognize the horizon line associated with a plane, and if our camera is calibrated, then we can estimate the orientation of that plane.
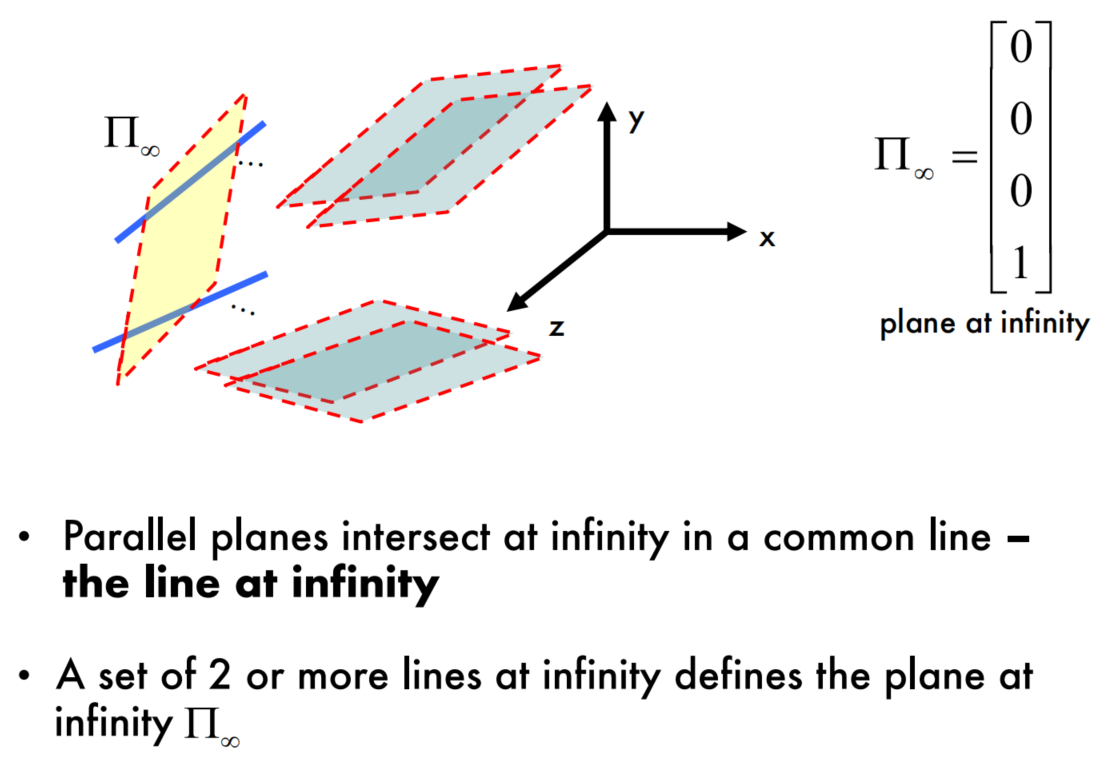
Planes at infinity
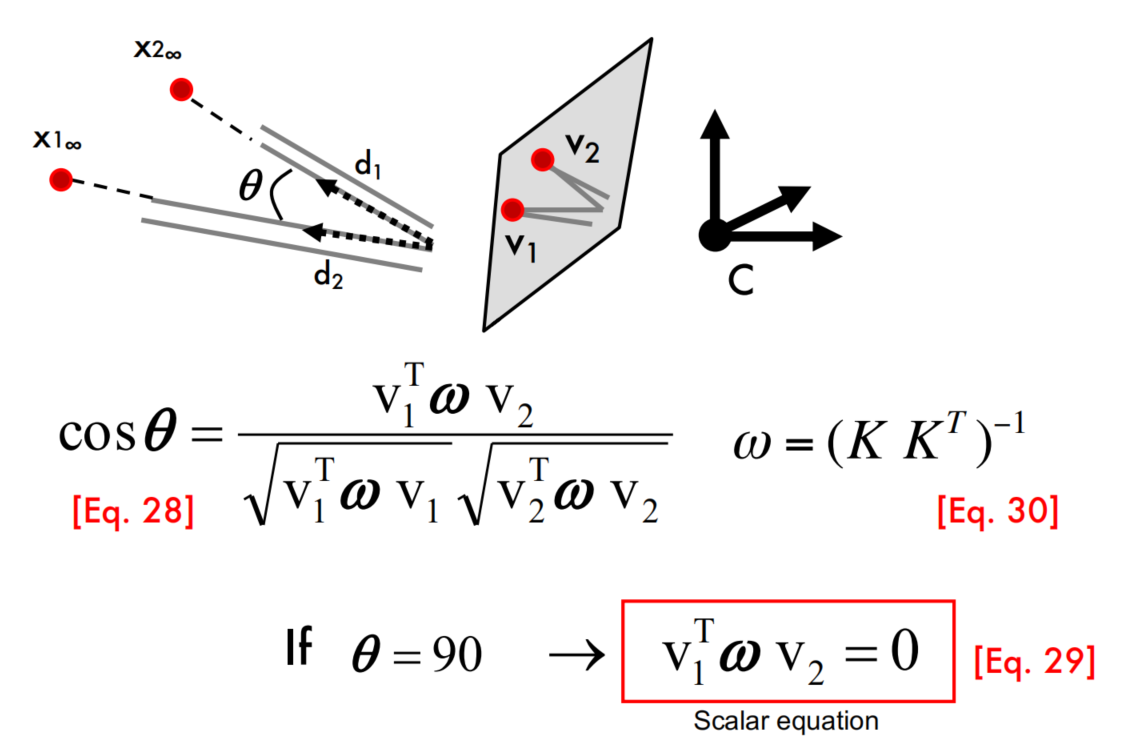
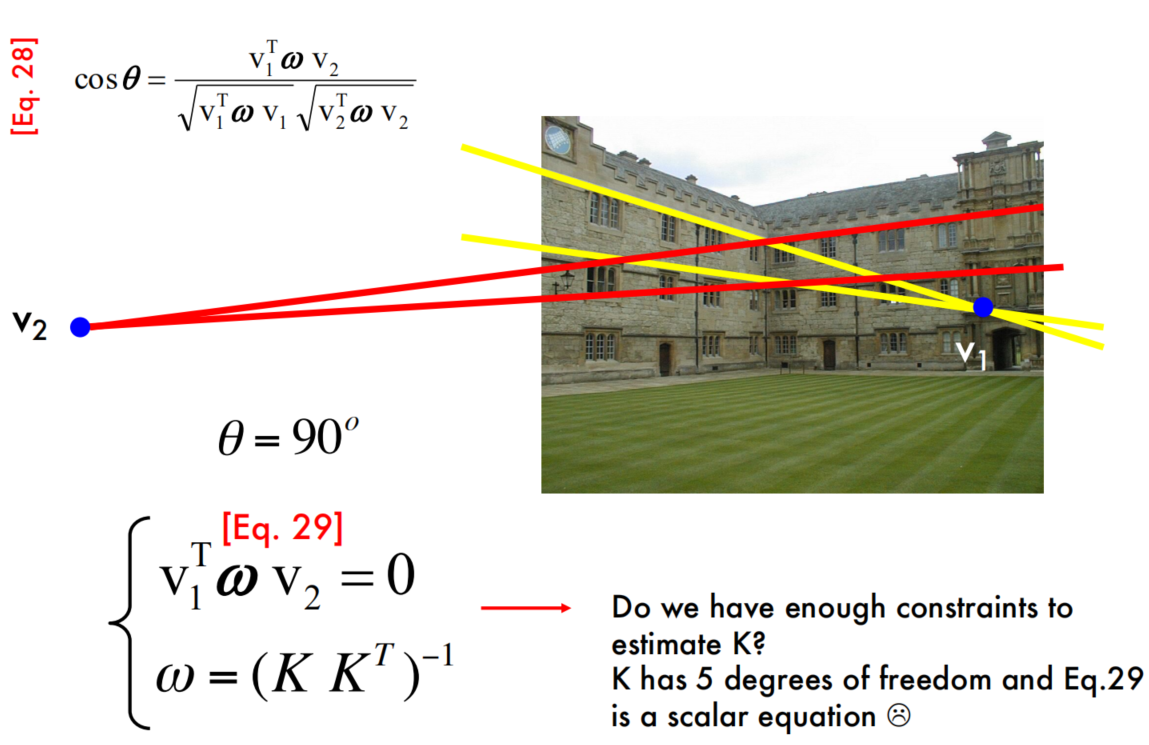
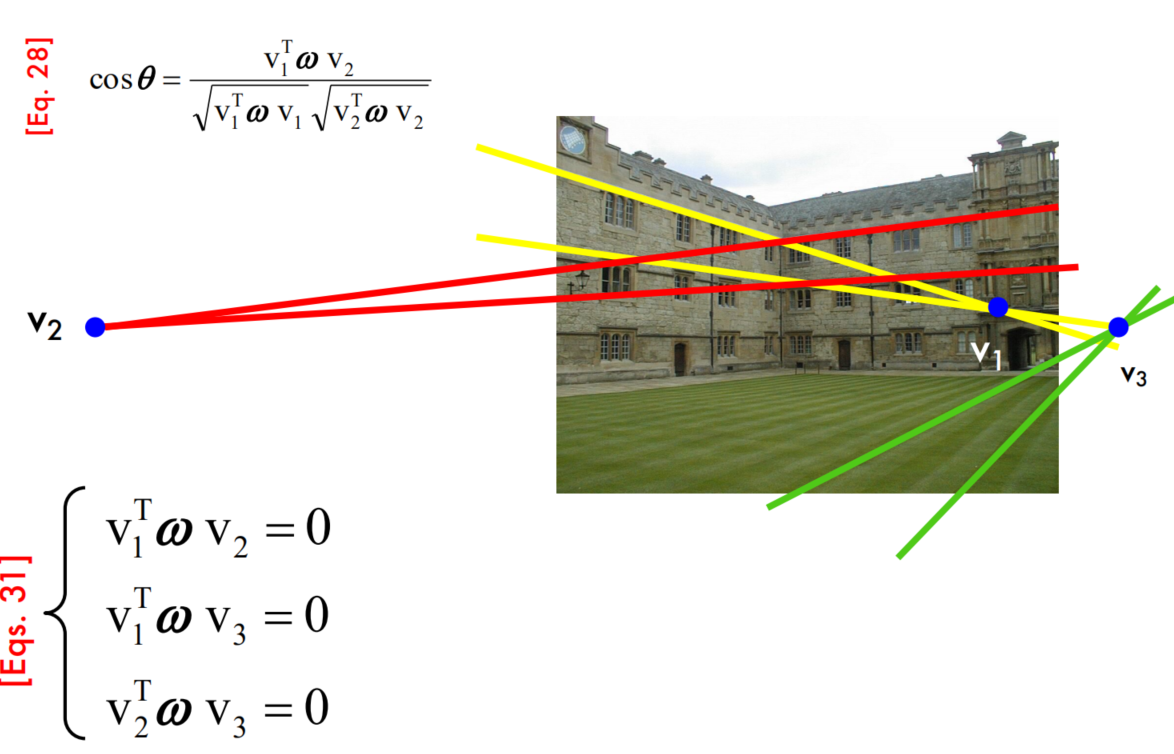
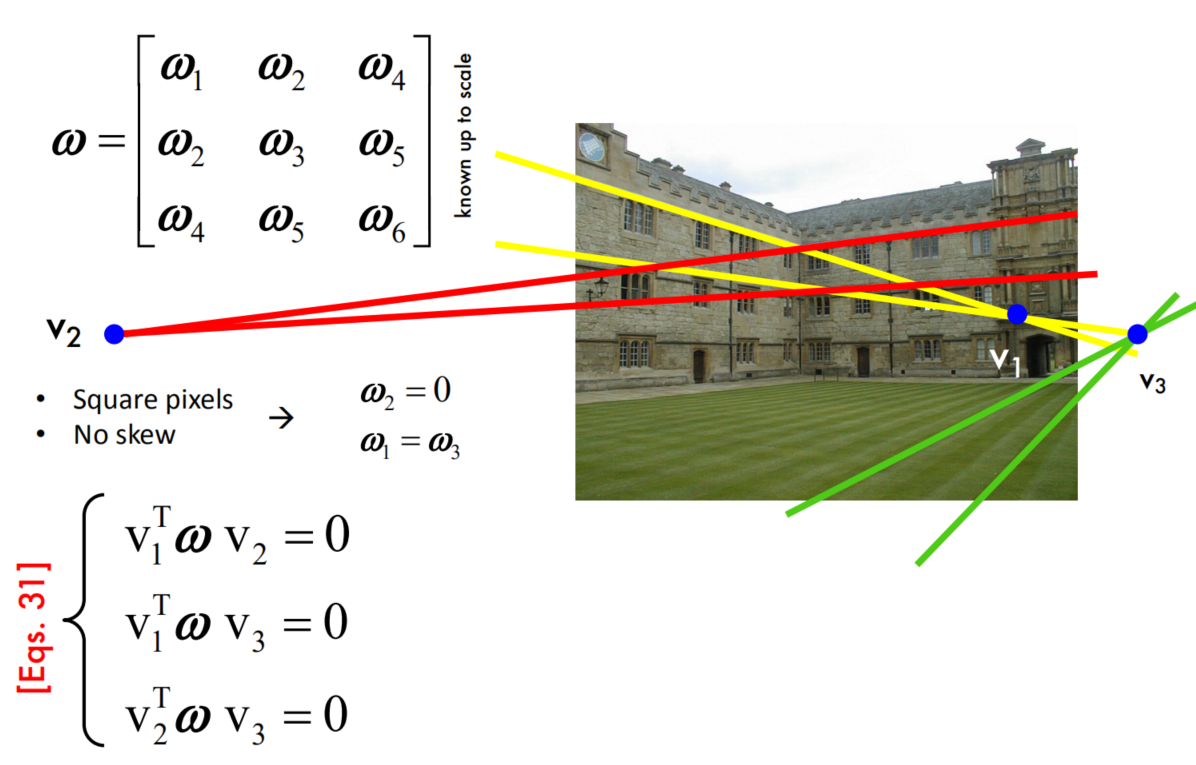
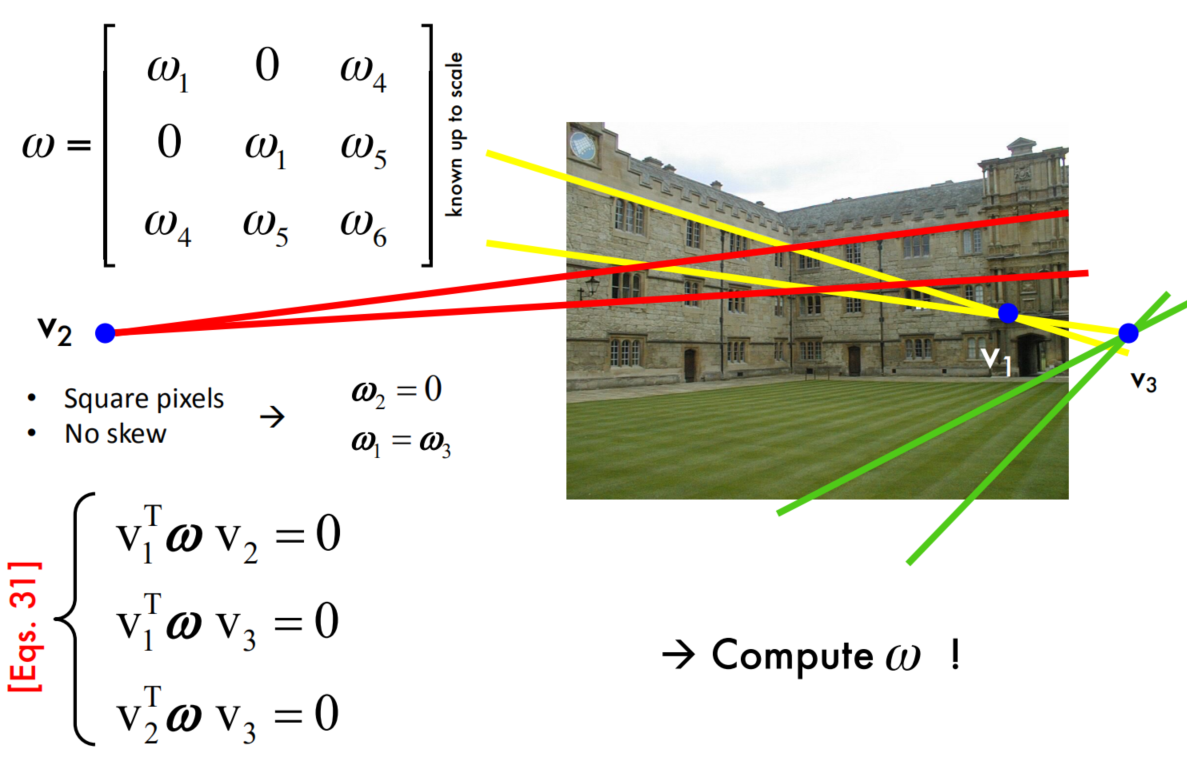
Angle between 2 vanishing points
Properties of $\omega$

Summary
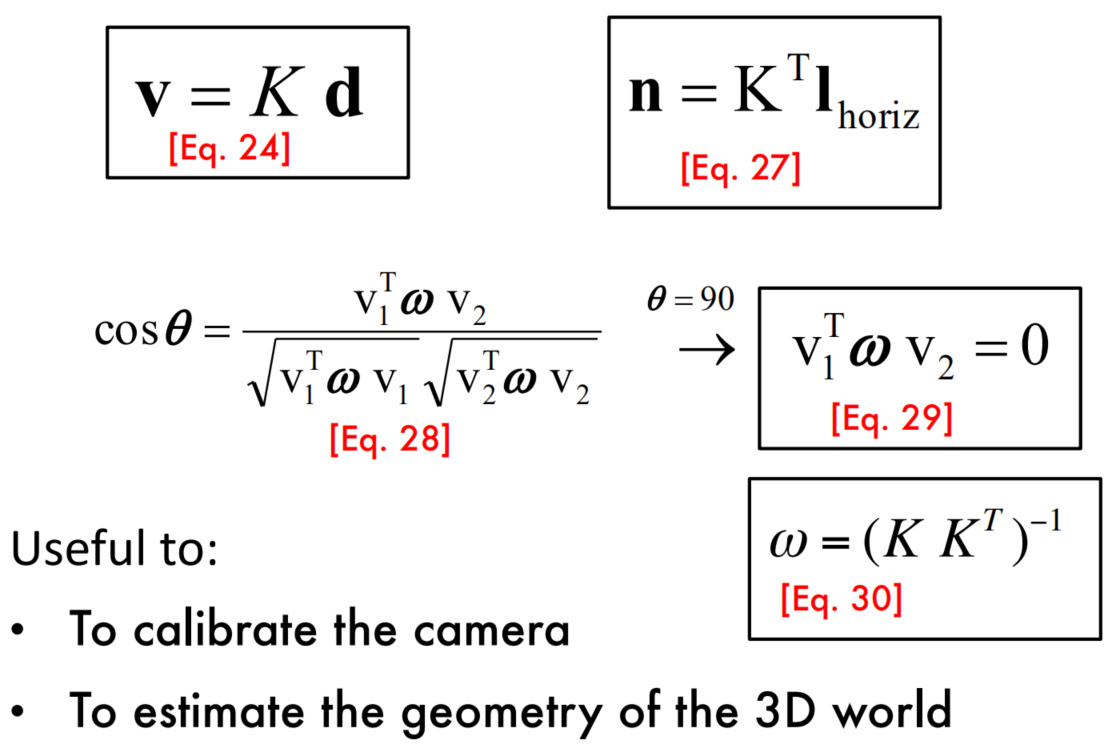
Questions
Q:为什么无穷远处的线$l_\infty=\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}$
A:有穷点显然不在$l_\infty$上,因此$\begin{bmatrix} x \\ y \\ 1 \end{bmatrix} l_\infty \neq 0$;无穷点显然应该在$l_\infty$上,因此$\begin{bmatrix} x \\ y \\ 0 \end{bmatrix} l_\infty = 0$。
Q:为什么3D中两条平行直线的交点与直线的方向向量是相同的
A:TODO(不过把两条直线的一般方程摆出来,确实就应该是直线的方向向量才满足条件)
Estimating geometry from a single image
Single view calibration - example
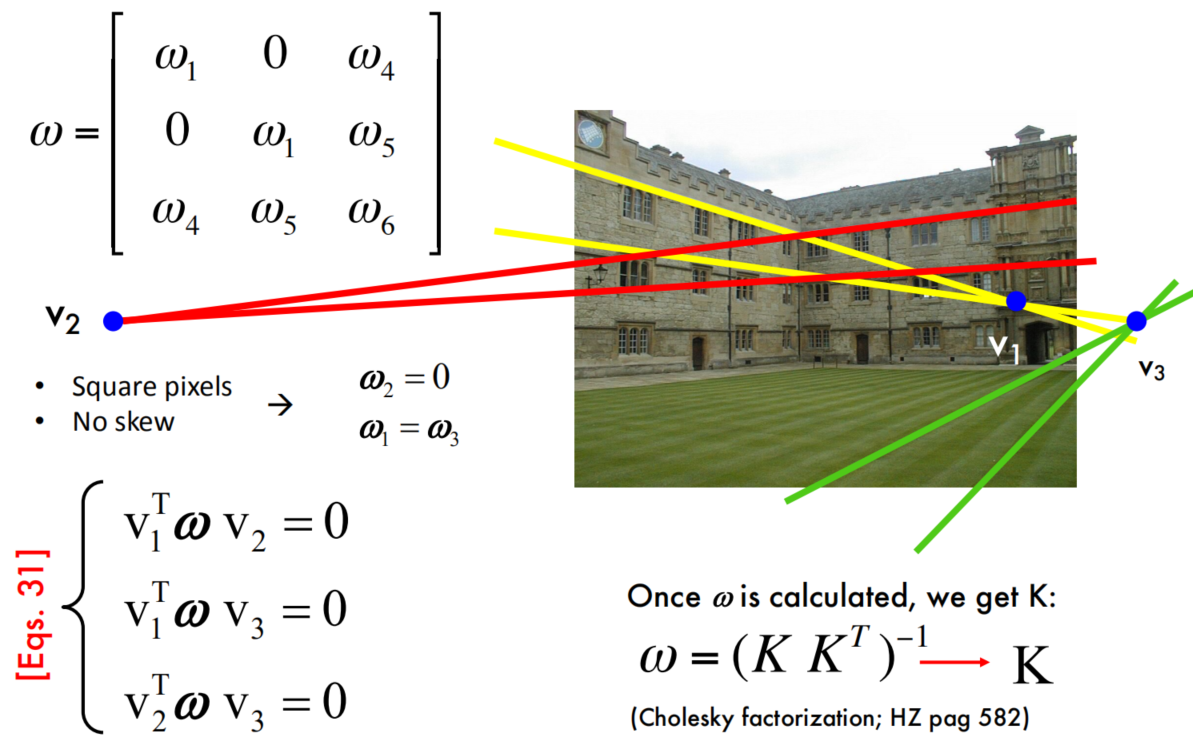
Single view reconstruction - example
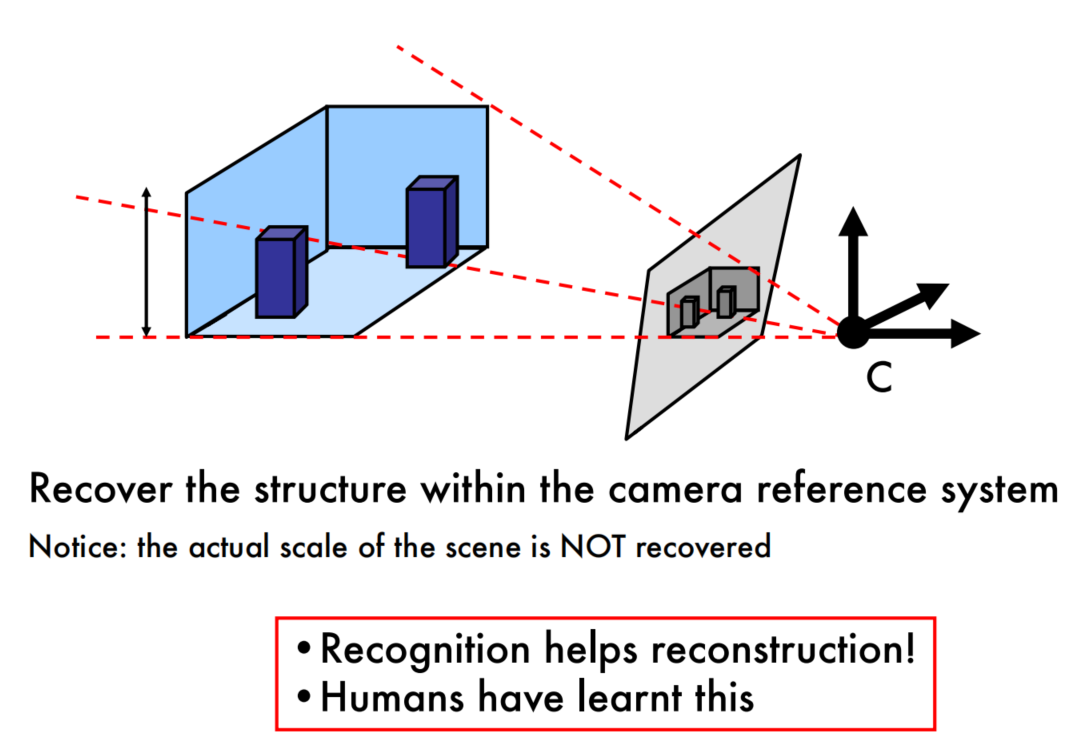
Single view reconstruction - drawbacks