CS231A Lecture 2: Camera Models
Reading:
[FP] Chapter 1, “Geometric Camera Models”
[HZ] Chapter 6 “Camera Models”
Pinhole cameras
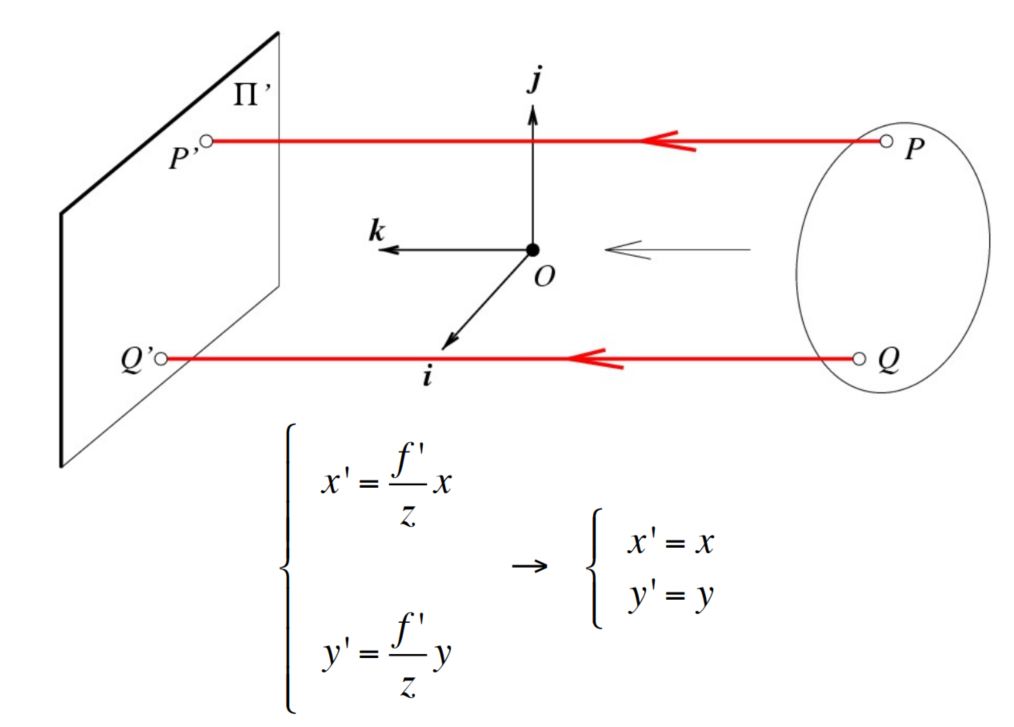
Pinhole Perspective
下面三张图描述的是:从世界坐标系到像平面坐标系的变换,物体最后投影到物理成像平面(image plane)上。
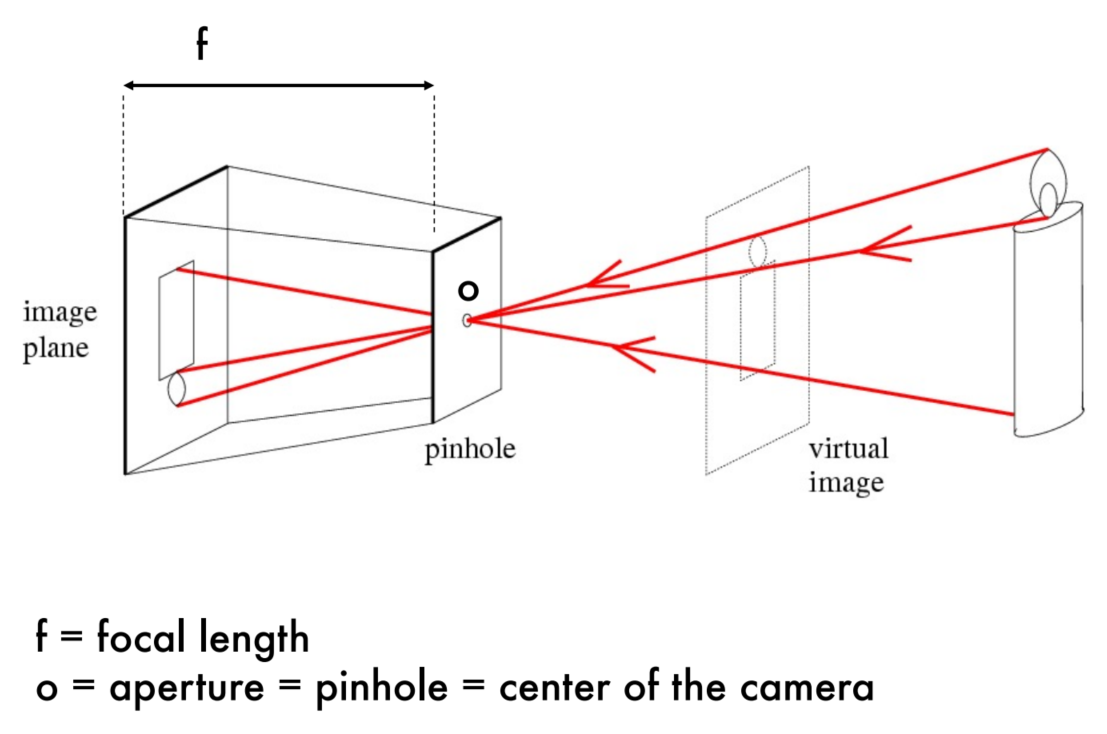
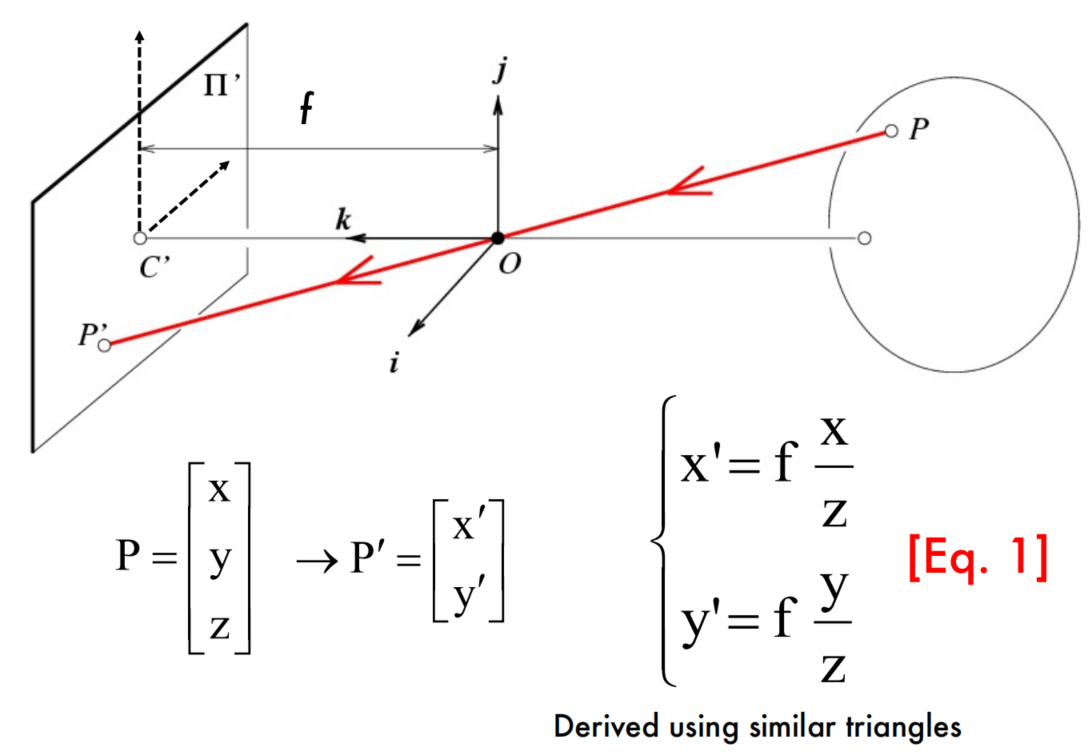
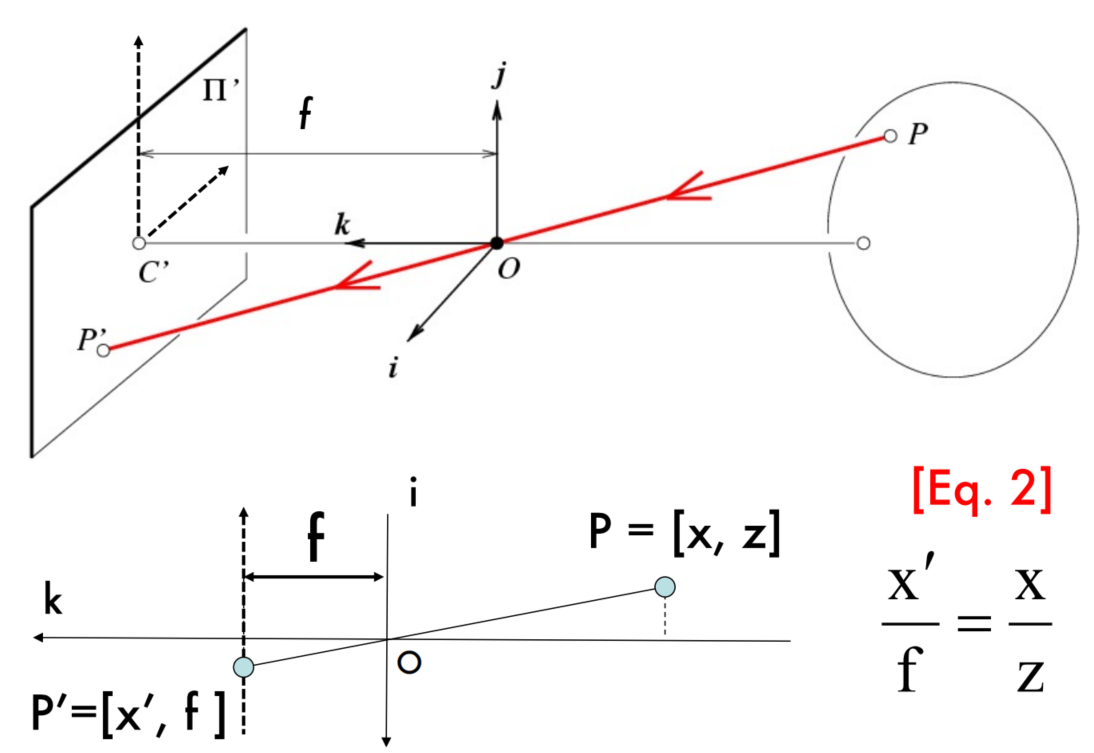
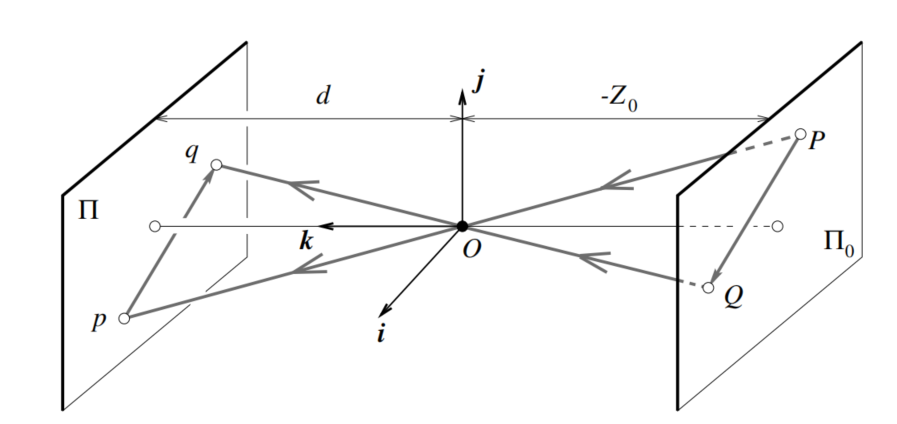
这种针孔透视有两个特点:a)远处的物体成的像更小;b)位于某平面中的两条平行线的投影似乎会聚在水平线h上,该水平线h是由成像平面与平行于某平面并穿过针孔的平面相交而形成的。注意,某平面中平行于成像平面的线根本没有图像。
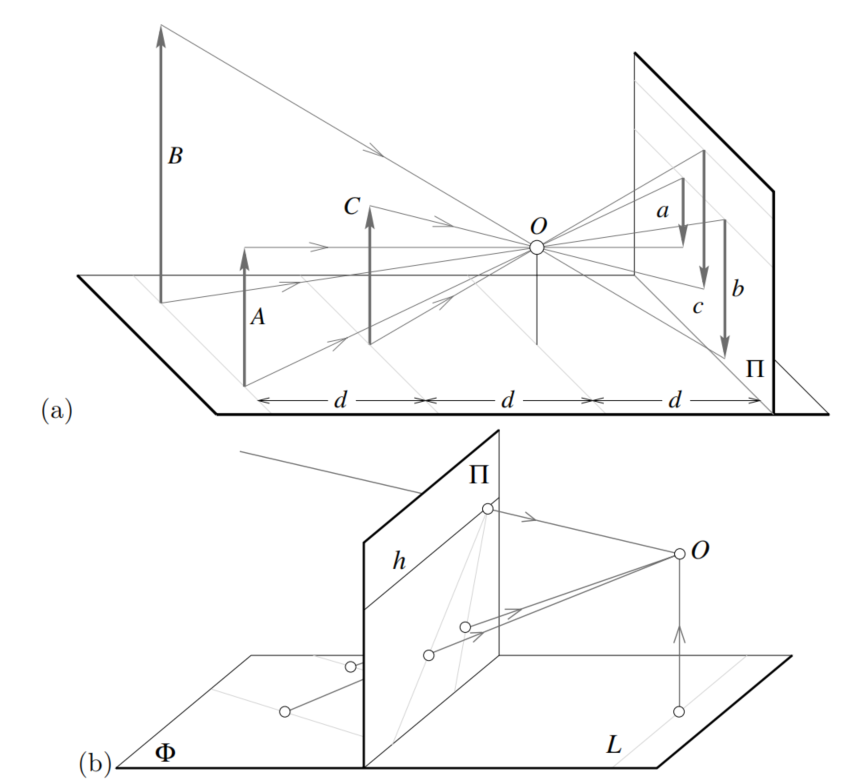
Weak Perspective
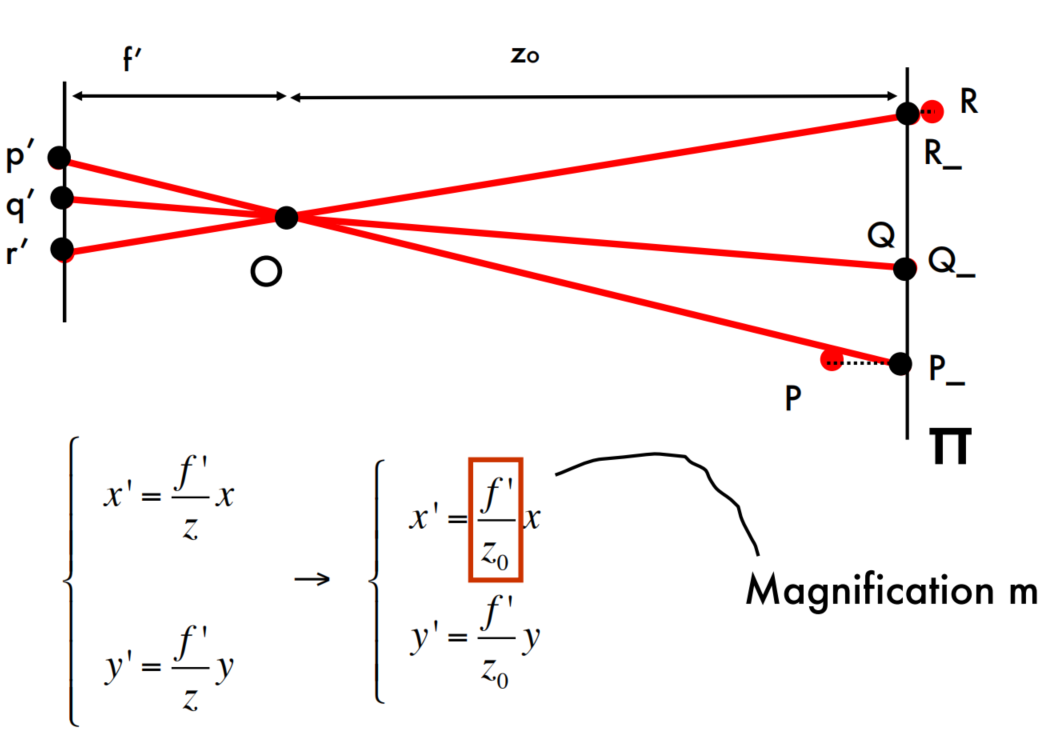
弱透视投影模型:针对于针孔成像模型做了进一步简化,物体投影时各个点与小孔的距离都用物体的平均距离代替,即不存在近大远小了,因为都是相同距离了。这样成像的大小就是成像平面与针孔距离d,以及物体与针孔距离D之间的比例决定了。这个模型对应的投影过程就称之为弱透视投影。
教材原话:When a scene’s relief is small relative to its average distance from the camera, the magnifification can be taken to be constant. This projection model is called weak perspective, or scaled orthography.
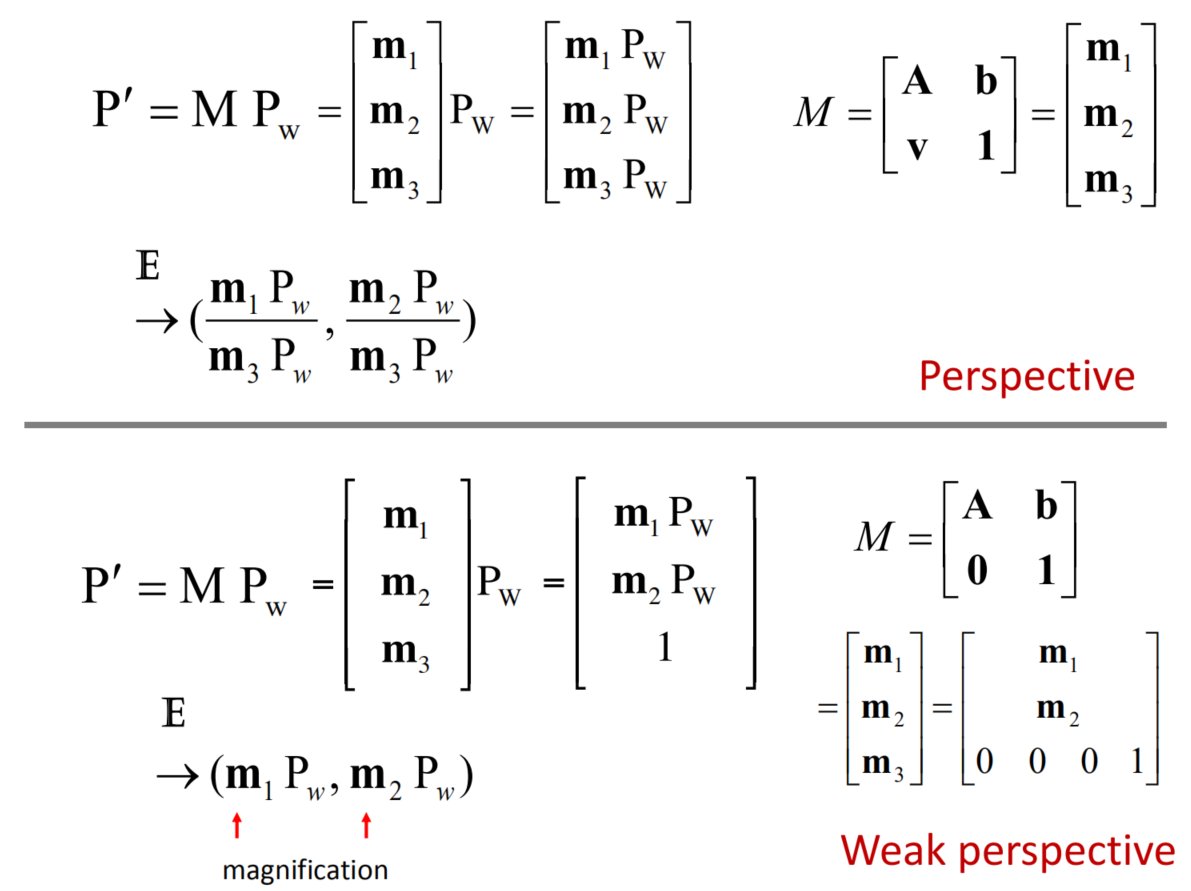
perspective与weak perspective的区别:
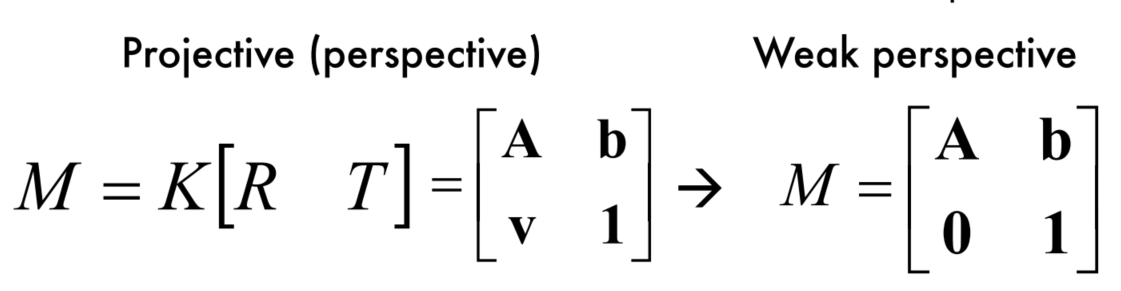
Orthographic projection
正交投影成像模型:在弱透视投影上进一步简化,让弱透视投影中仅存的比例为1,其效果等同于平行光线投射到成像平面上。这个模型对应的投影过程称之为正交投影。正交投影不涉及图像特征的反转,因此,放大倍数为负值,这有点不自然,但简化了投影方程。
Questions
Q:Is the size of the aperture(光圈,孔径) important?
A:光圈越大,成像越模糊;光圈越小,成像越清晰,但会越来越暗,因为透过的光线更少了(还有可能发生衍射)。
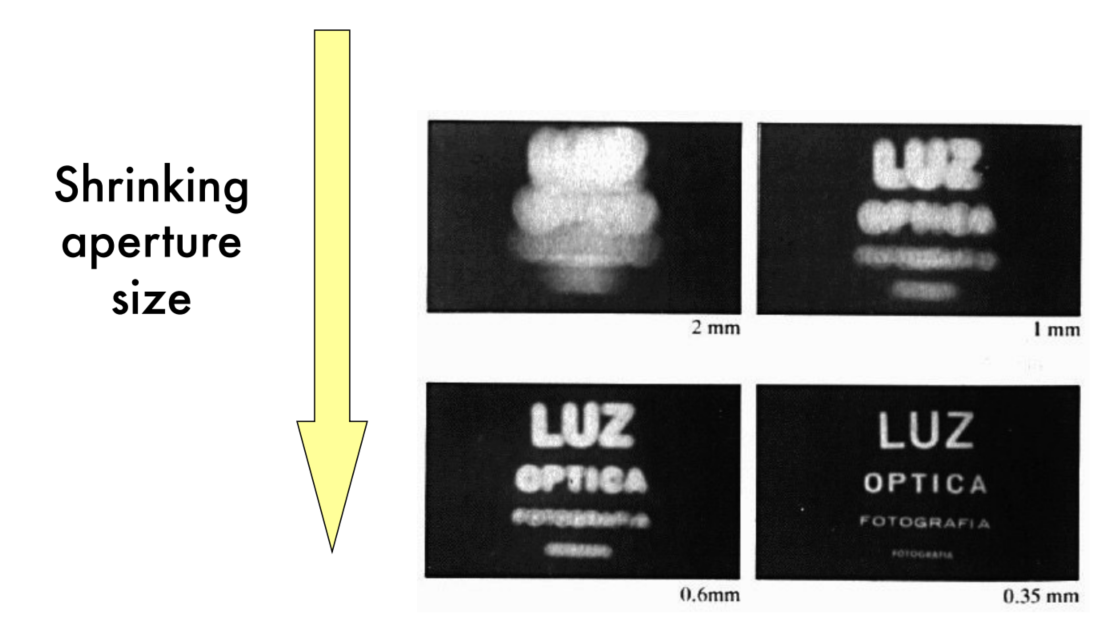
Q:如何应对透过光线更少的问题?
A:Adding lenses! (通过添加透镜将光线汇聚到胶片上)
Q:Pros and Cons of These Models
A:

Cameras & lenses
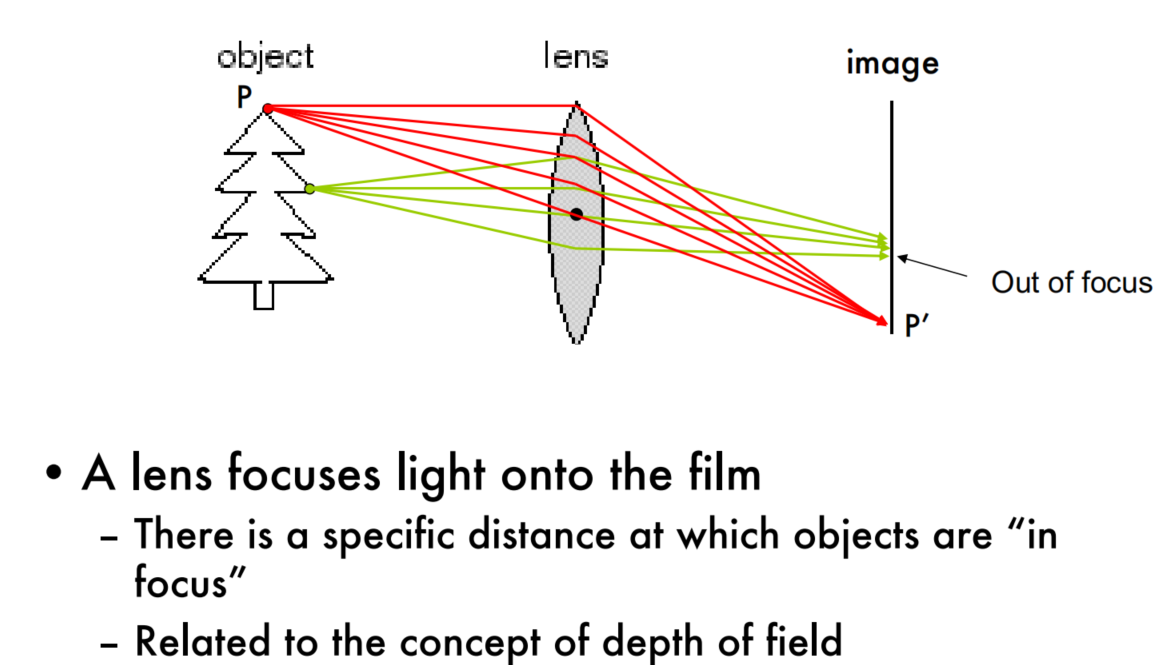
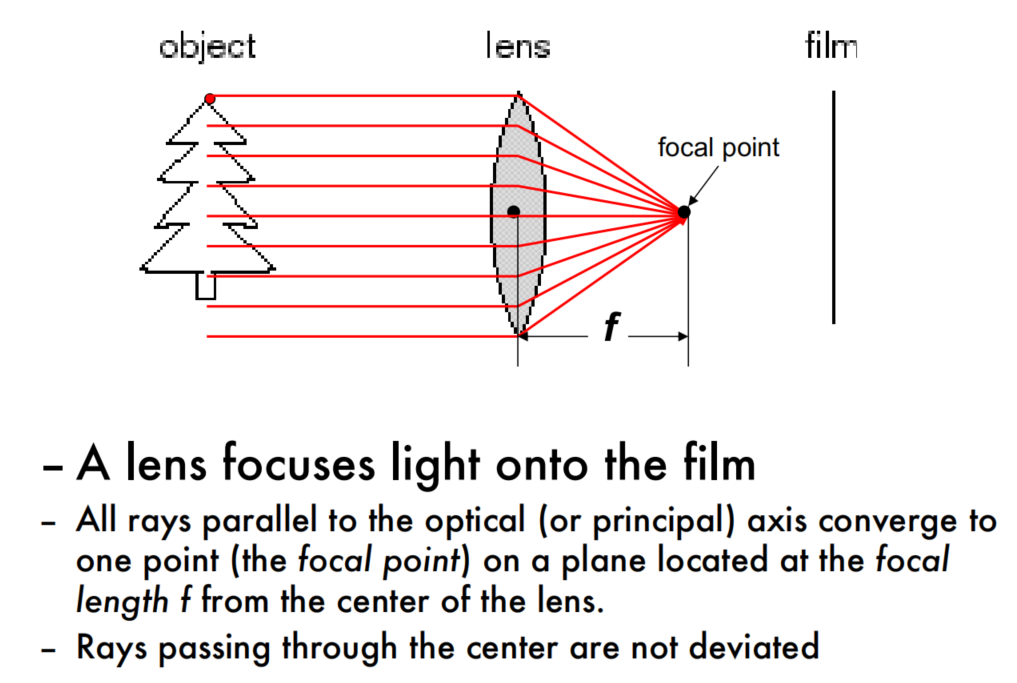
A lens focuses light onto the film
Paraxial refraction model
近轴折射模型
下面的ppt主要表达了一个点,即相机的焦距依然是小孔到成像平面的距离,它和透镜的焦距有区别!(相机焦距还可以计算出来,经典的初中物理题。。。)
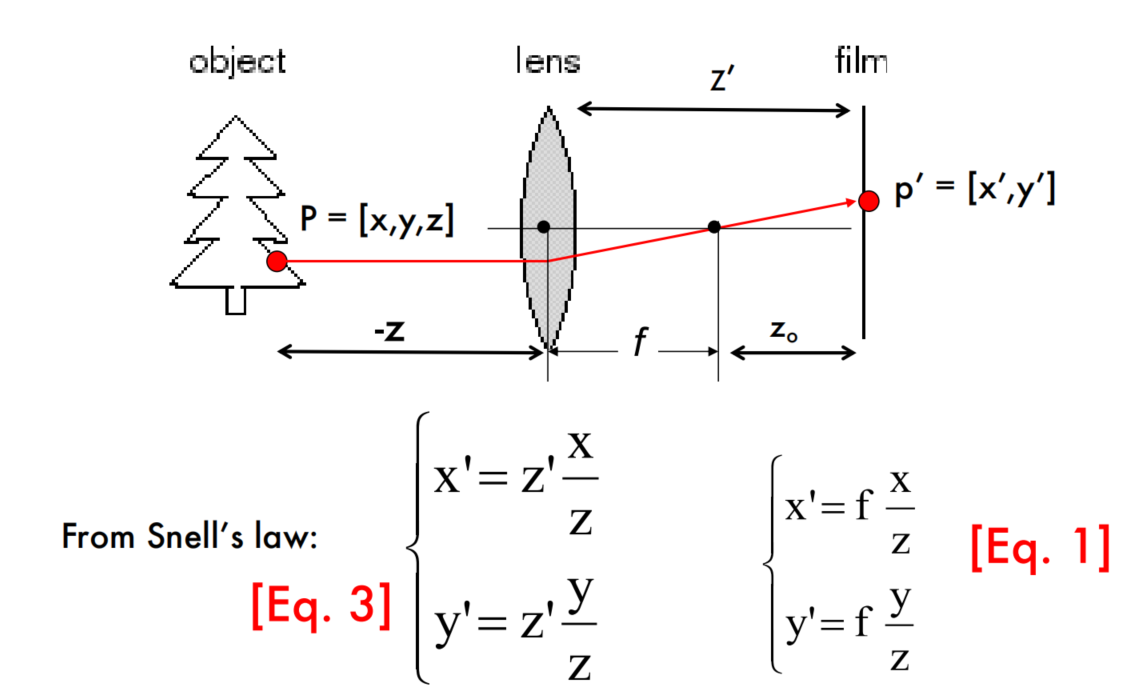
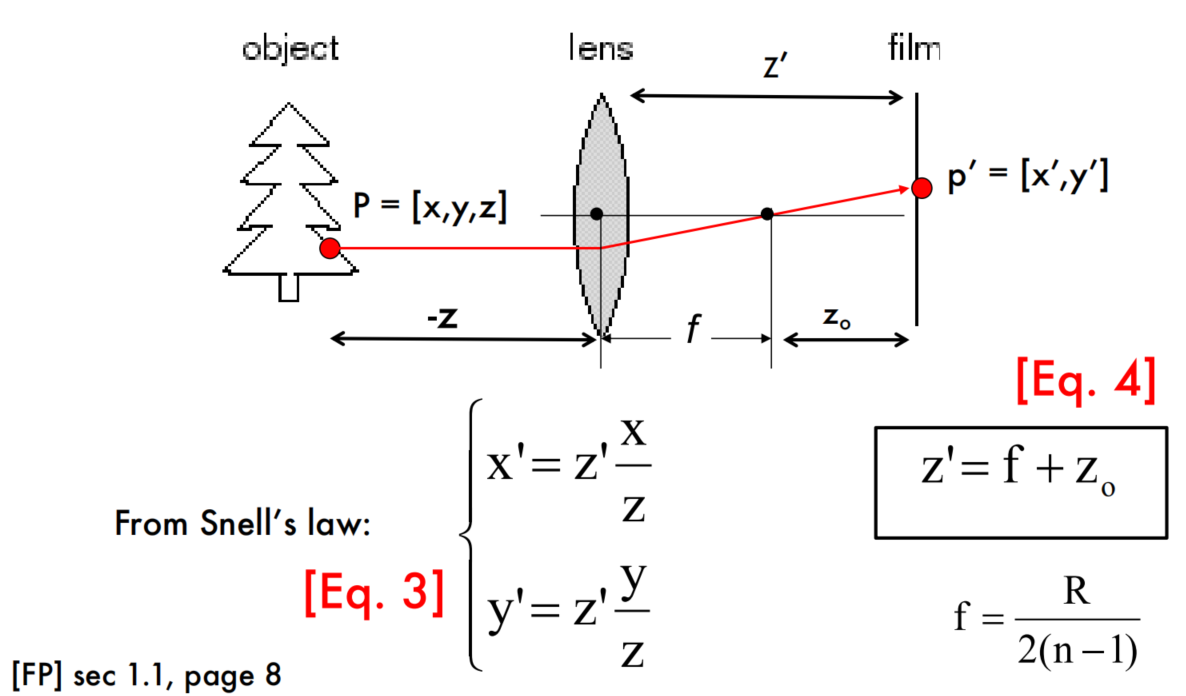
Questions
Q:为什么相机需要装透镜?
A:在教材上有这么一句话:“Most real cameras are equipped with lenses. There are two main reasons for this: The first one is to gather light, because a single ray of light would otherwise reach each point in the image plane under ideal pinhole projection. Real pinholes have a finite size, of course, so each point in the image plane is illuminated by a cone of light rays subtending a finite solid angle. The larger the hole, the wider the cone and the brighter the image, but a large pinhole gives blurry pictures. Shrinking the pinhole produces sharper images but reduces the amount of light reaching the image plane, and may introduce diffraction effects. Keeping the picture in sharp focus while gathering light from a large area is the second main reason for using a lens.”
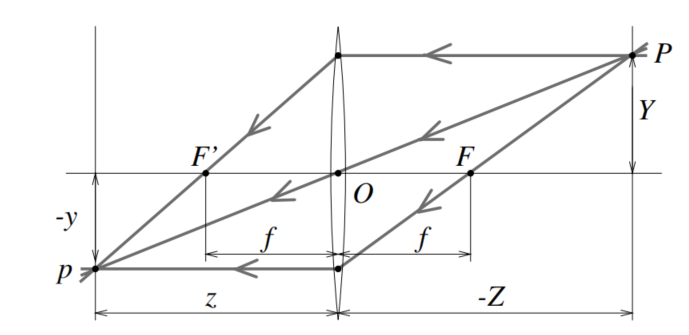
Q:透镜是如何聚集光线的?
A:如下图所示。
Q:相机的针孔和透镜的关系?有了透镜之后还需要针孔吗?
A:我的理解是,透镜中心点O就是所谓的针孔。
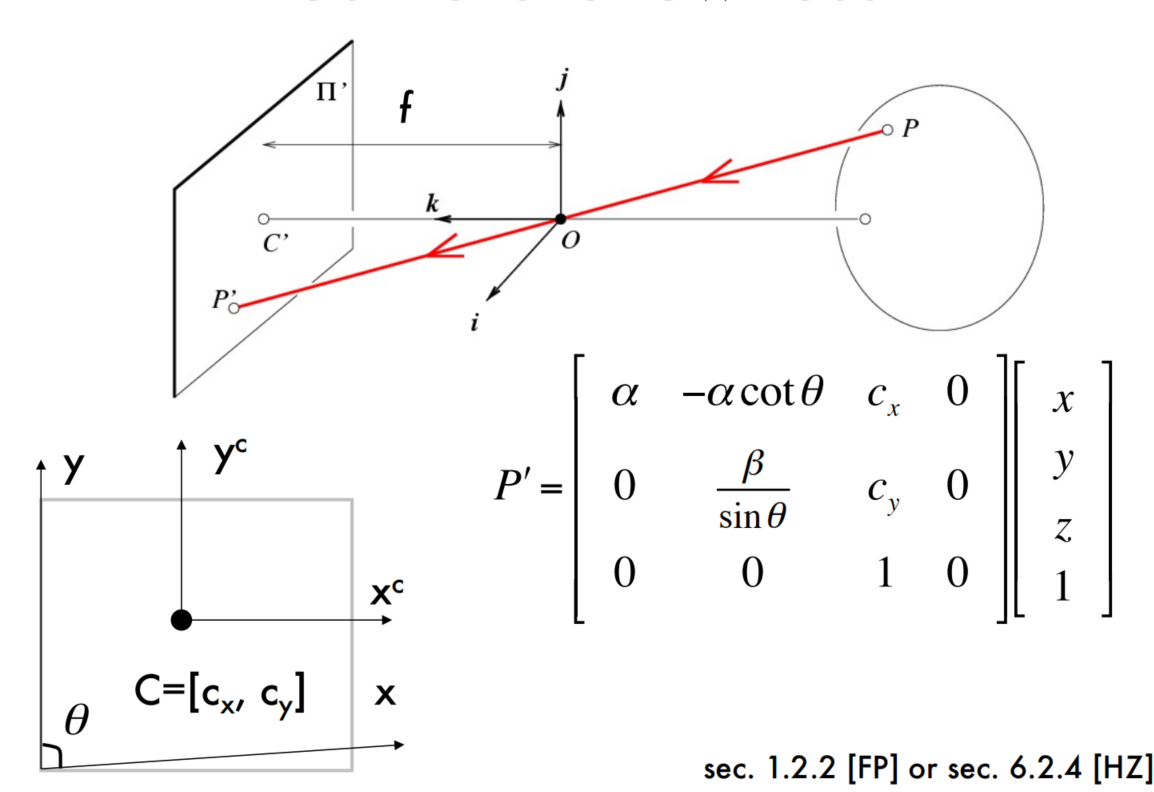
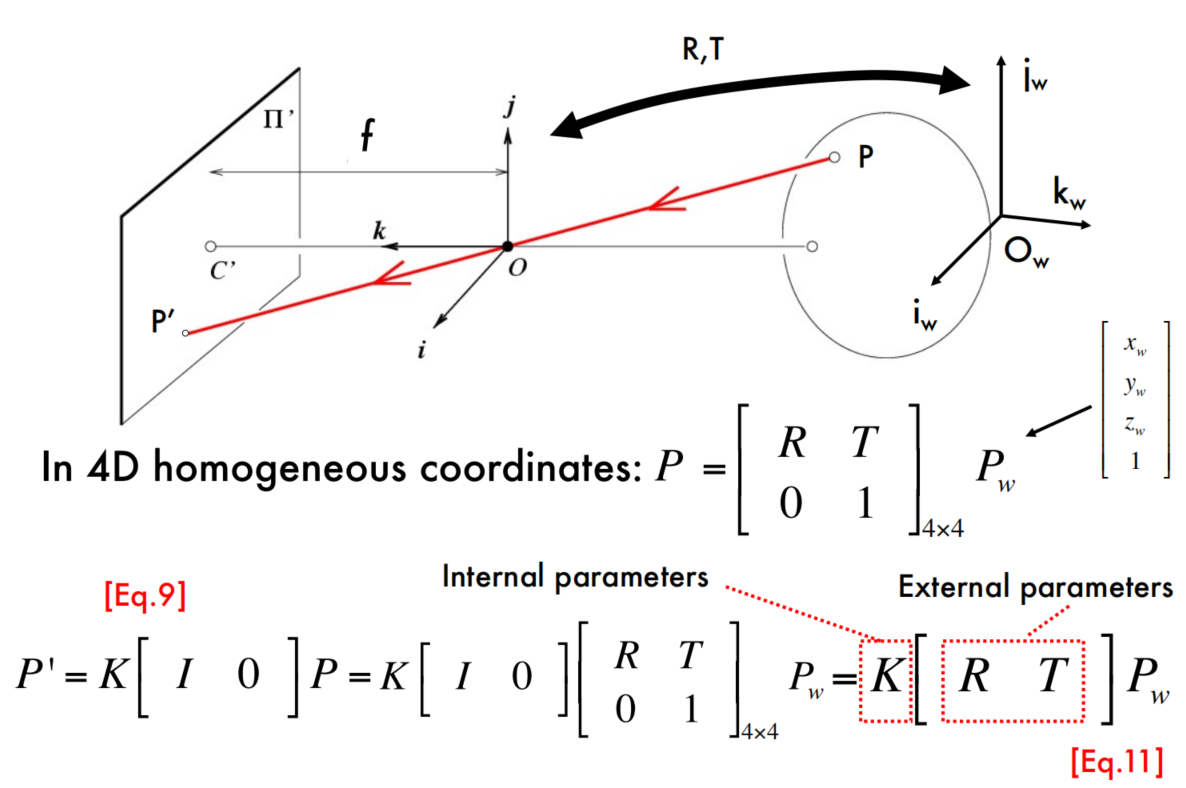
The geometry of pinhole cameras-Intrinsic
Converting to pixels
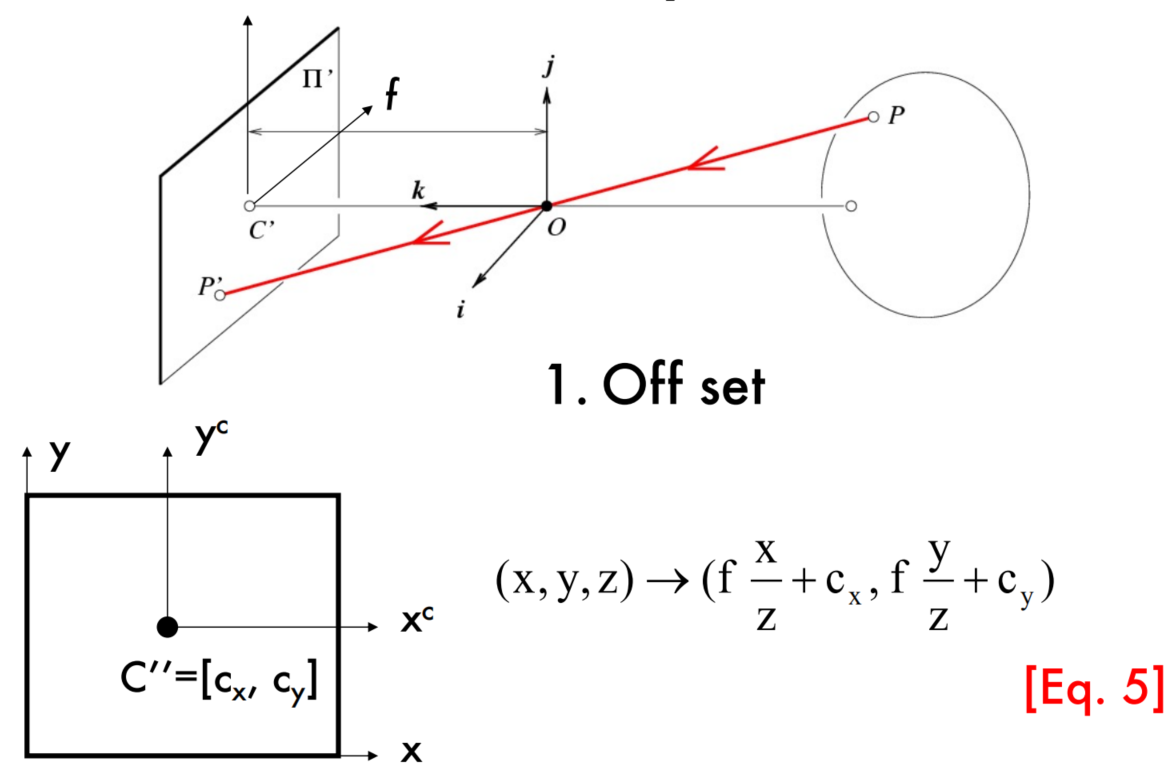
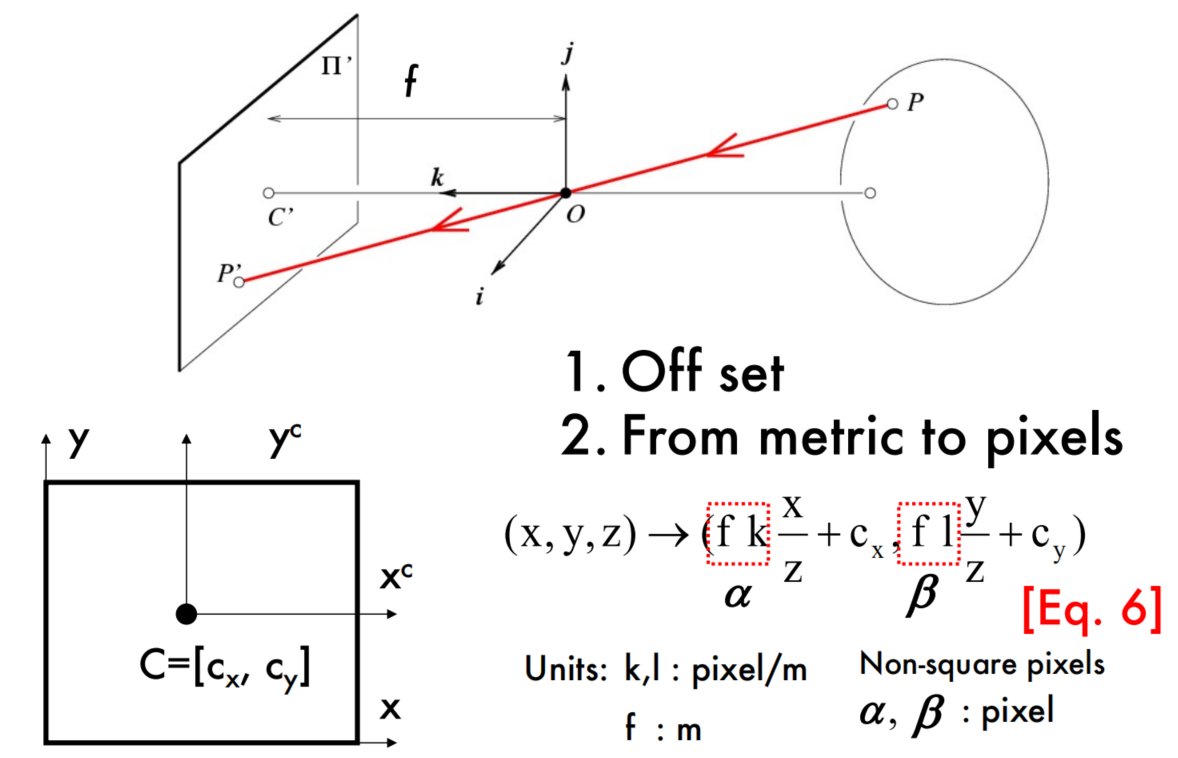
Homogeneous coordinates

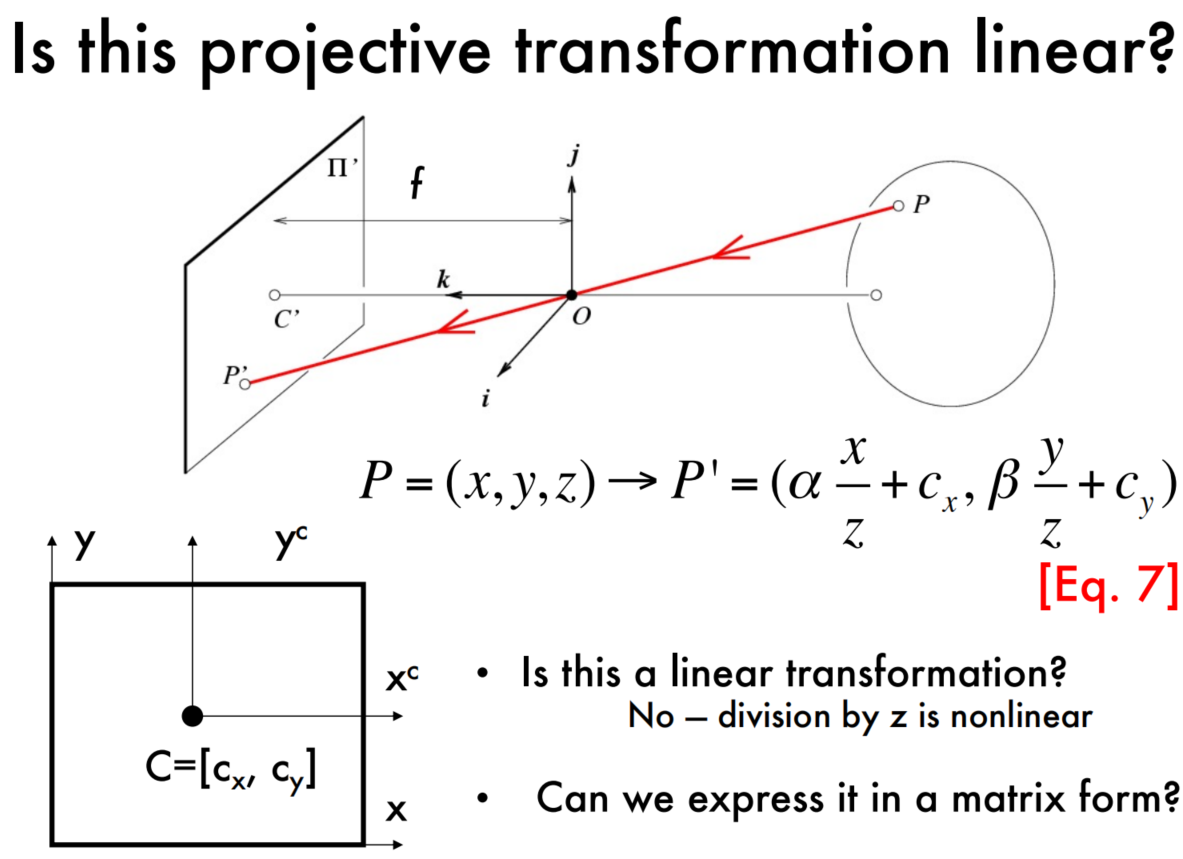
Projective transformation in the homogenous coordinate system
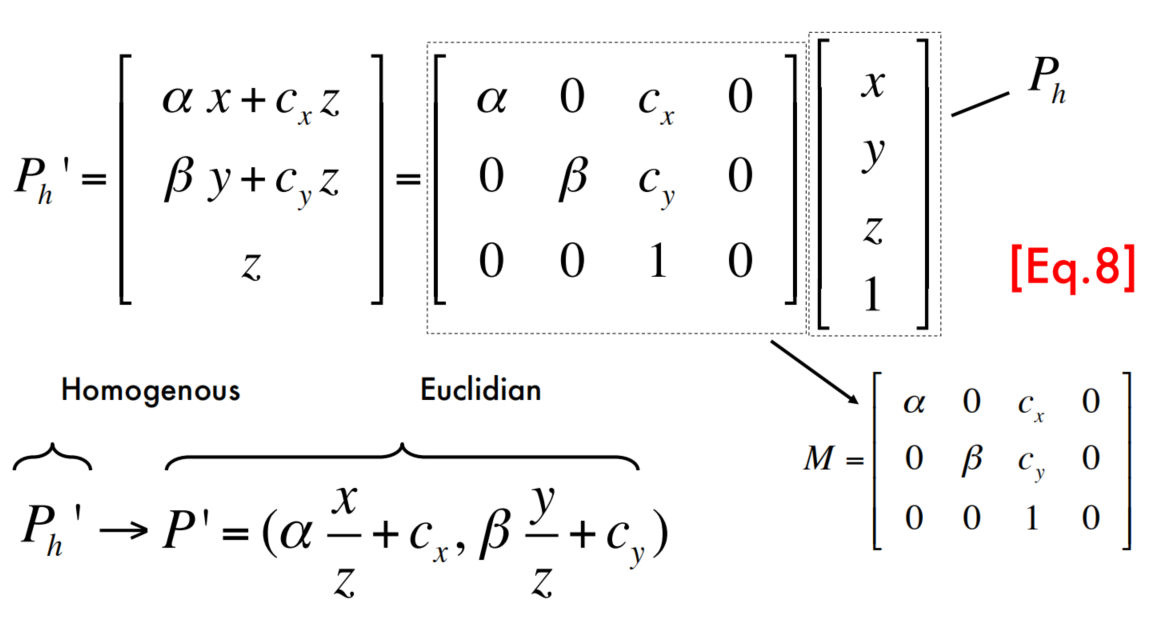
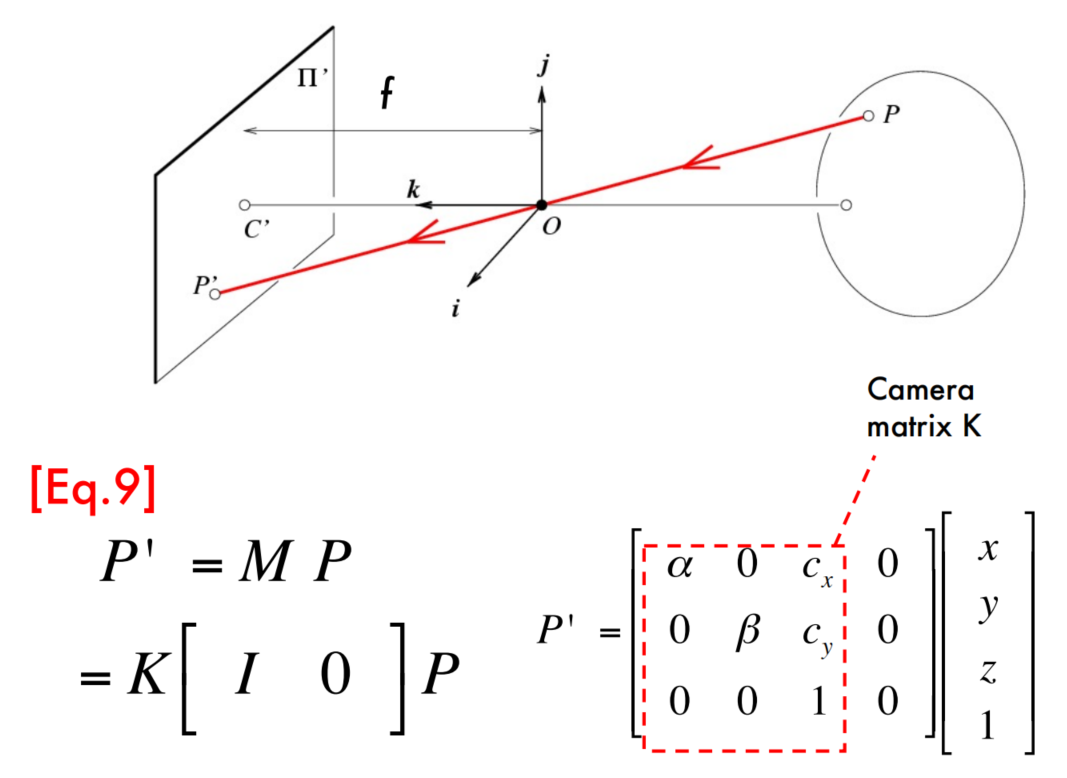
The Camera Matrix
Camera Skewness
How many degrees of freedom does K have?
5 degrees of freedom!
Question
Q:为什么相机内参K有五个自由度?
A:矩阵K中有五个互相独立的变量!
The geometry of pinhole cameras-Extrinsic
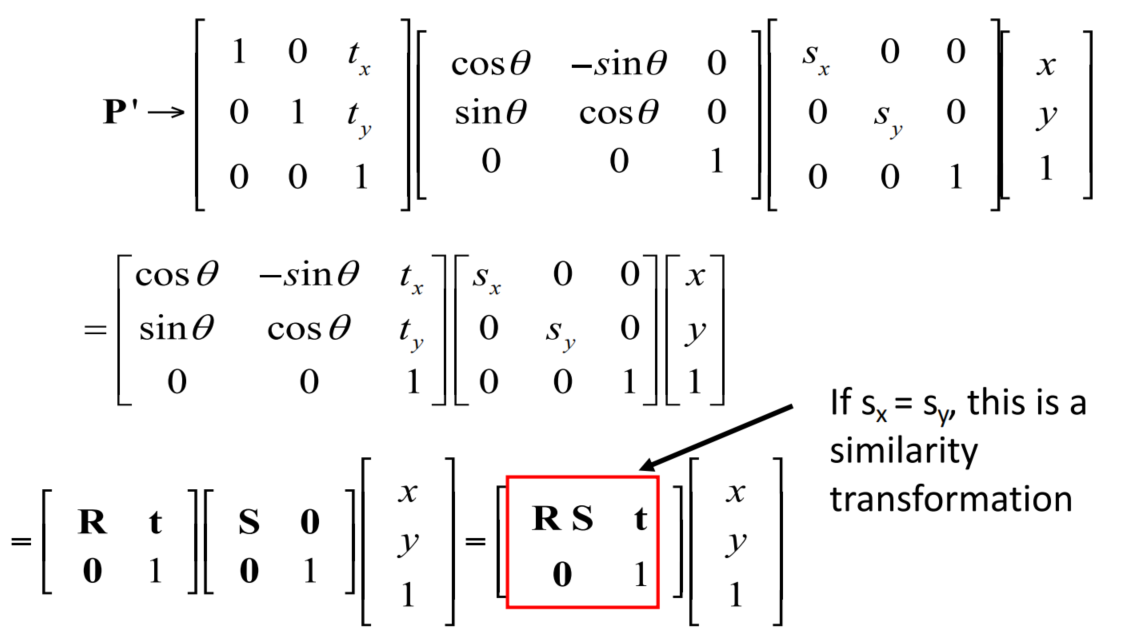
2D Scale + Rotation + Translation
3D Translation and Rotation
3D Rotation of Points

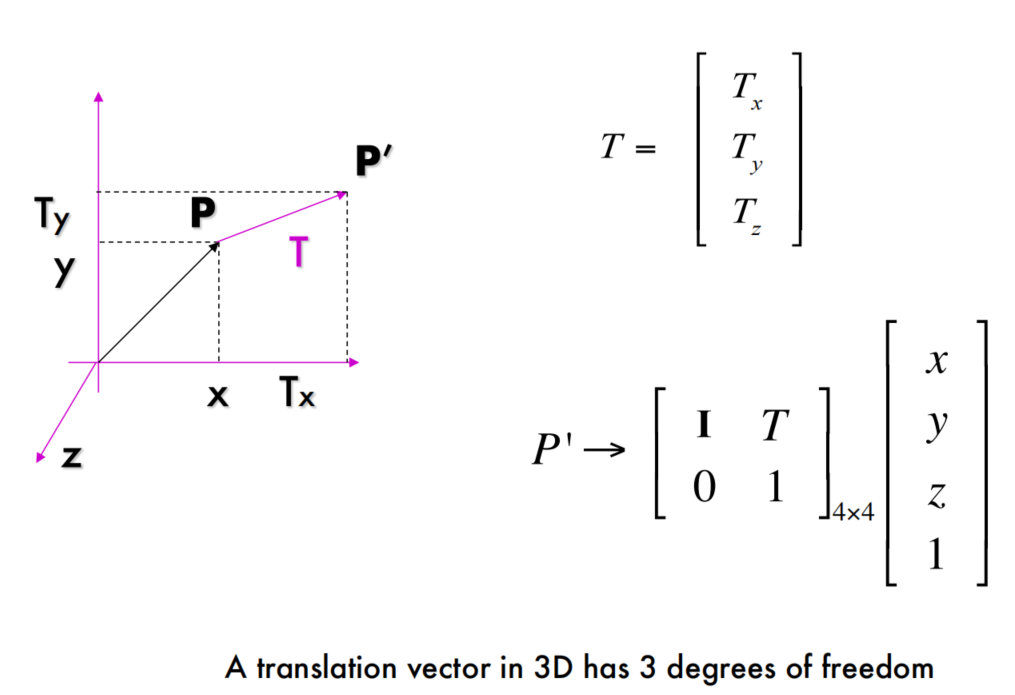
3D Translation of Points
Translation and Rotation
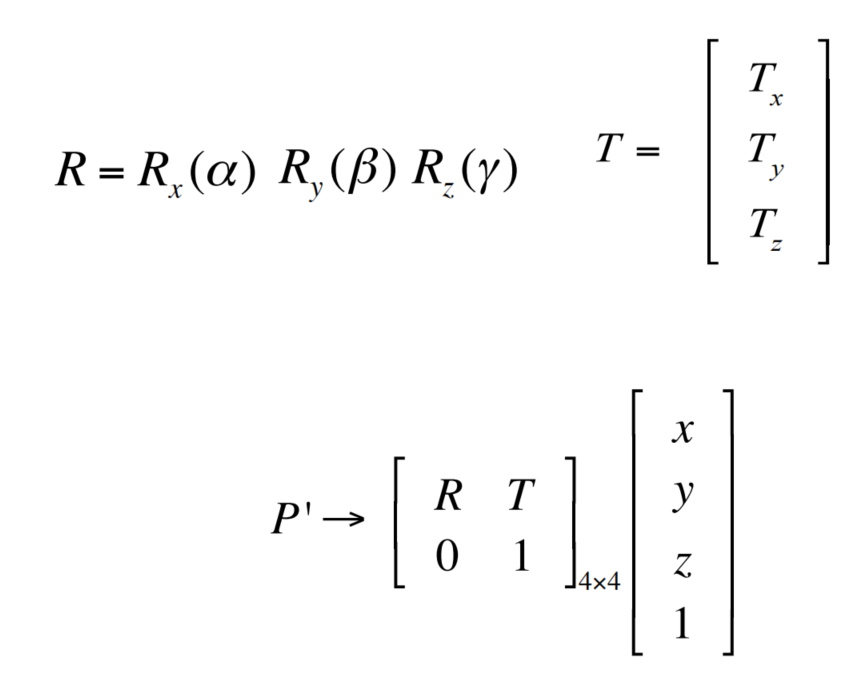
World reference system
The projective transformation
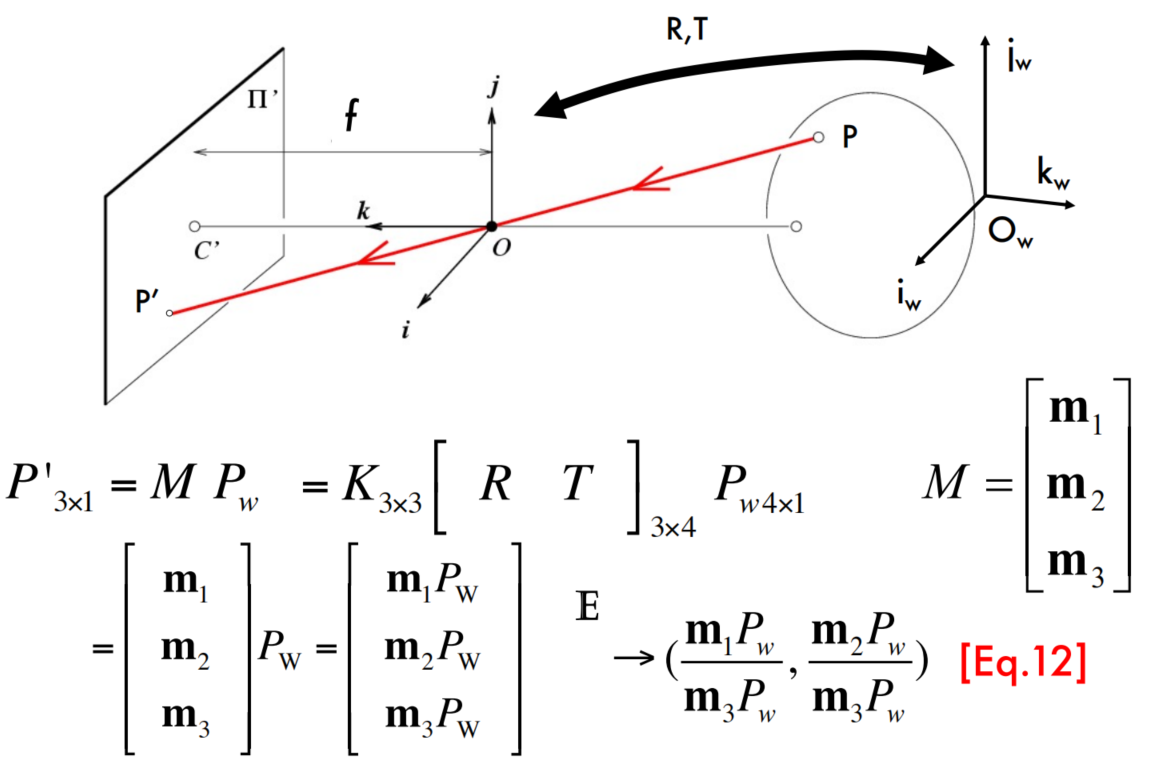
How many degrees of freedom does M have?
5 + 3 + 3 =11
Perspective Projection Matrices

Camera distortion
该部分参考:https://xhy3054.github.io/camera-calibration-undistort
现代相机为了获得更好的成像效果,相机里一般都加入了透镜。而透镜的加入对成像过程中光线的传播会产生新的影响,进而出现畸变,一般有两种主要的畸变(其实也还有其他的种类的畸变,但是不如这两种明显):
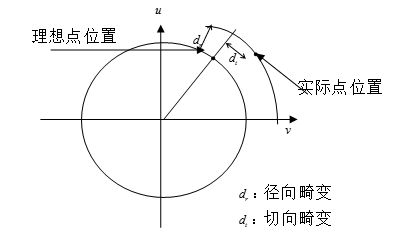
Radial Distortion
径向畸变:透镜自身的形状对光线传播会有影响;
- 桶形畸变:图像放大率随着与光轴之间的距离增加而减小
- 枕形畸变:图像放大率随着与光轴之间的距离增大而增大

一般径向畸变对于二维平面上一个坐标$(x,y)$(如上图畸变最小的点为坐标原点,一般在图像中心,$r$是点到原点的距离)的影响可以使用如下公式表述:
$$
x_{distorted} = x( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6)
\\
y_{distorted} = y( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6)
$$
无论是桶形畸变还是枕形畸变,由于他们都是随着与中心之间的距离增加而增加,因此可以使用一个多项式函数来描述畸变前后的像素坐标变化。
这个公式中,对于畸变较小的图像中心区域,畸变主要是$k_1$在起作用;而对于畸变较大的边缘区域,主要是$k_2$在起作用。一般的普通摄像头用这两个系数就已经可以很好地纠正径向畸变了,但是对于一部分畸变很大的摄像头,比如说鱼眼镜头等,还需要加入$k_3$畸变项才能比较好的表述畸变情况。
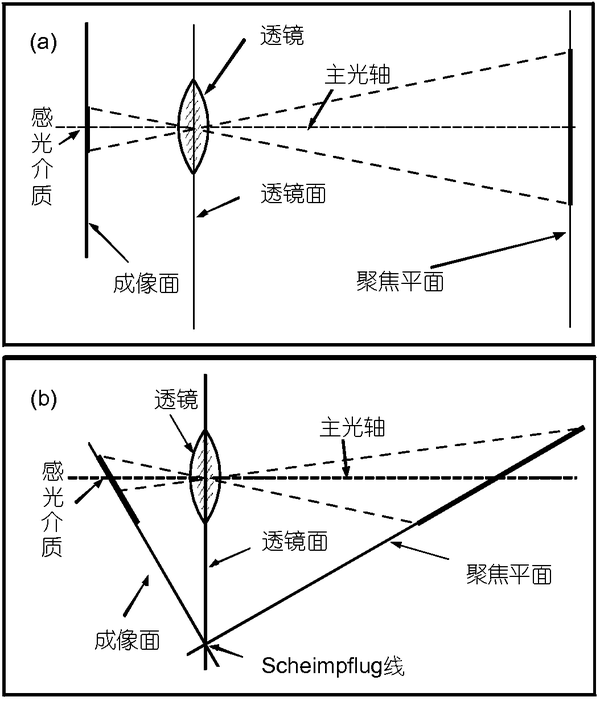
Tangential distortion
切向畸变:在机械组装过程中,透镜和成像平面不可能完全平行,这也会使得光线穿过透镜投影到成像面时的位置出现变化;
一般切向畸变对于二维平面上的坐标(x,y)的影响可以使用如下公式进行表述:
$$
x_{distorted} = x + 2p_1xy + p_2(r^2+2x^2)
\\
y_{distorted} = y + p_1(r^2+ 2y^2)+ 2p_2xy
$$
Radial and tangential distortion
结合上面两种径向畸变和切向畸变的公式,可以得到综合的去畸变公式,也就是说我们通过五个畸变系数就可以确定点在像素平面的正确位置。
$$
x_{distorted} = x( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + 2p_1xy + p_2(r^2+2x^2)
\\
y_{distorted} = y( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + p_1(r^2+ 2y^2)+ 2p_2xy
$$



