机器学习笔记(六):深入理解卷积神经网络
一、卷积计算层CONV
1.1 什么是“卷积”?
什么是卷积:
图像中不同数据窗口的数据和卷积核(一个滤波矩阵)作内积的操作叫做卷积。
简单来说,卷积(或称内积)就是“对应相乘,再结果累加”。
卷积的计算过程又称为滤波(filter),本质是提取图像不同频段的特征。
1.2 什么是“卷积核”?
什么是卷积核:
卷积核也称为滤波器filter,带着一组固定权重的神经元,通常是n*m二维的矩阵,n和m也是神经元的感受野。n*m 矩阵中存放的是对感受野中数据处理的系数。
一个卷积核的滤波可以用来提取特定的特征(例如可以提取物体轮廓、颜色深浅等)。
通过卷积层从原始数据中提取出新的特征的过程,又成为feature map(特征映射)。
举例说明:
【1】比如,我现在要训练一个最简单的CNN,用来识别一张图片里的字母是X还是O

人眼一看,很简单,明显就是X,但是计算机不知道,它不明白什么是X。所以,我们给这张图片加一个标签,也就是俗称的Label,Label=X,就告诉了计算机这张图代表的是X。计算机就记住了X的长相。
【2】但是并不是所有的X都长这样。
比如说…

这四个都是X,但它们和之前那张X明显不一样,计算机没见过它们,又都不认识了。
【3】不认识了怎么办?
当然是计算机‘回忆’是不是见过差不多的。——这时候CNN要做的,就是如何提取内容为X的图片的特征。
我们都知道,图片在计算机内部以像素值的方式被存储。
也就是说,两张X在计算机看来,其实是这样子的。其中1代表白色,-1代表黑色


如果按照每像素逐个比较,肯定是不科学,结果不对而且效率低下,因此提出其他匹配方法。
观察这两张X图,可以发现尽管像素值无法一一对应,但也存在着某些共同点。如下图所示,两张图中三个同色区域的结构完全一致!
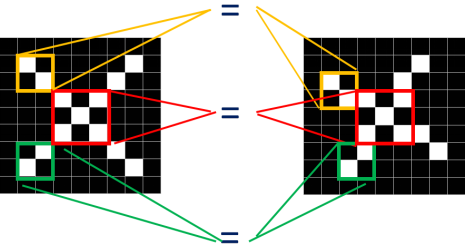
Q: 要将这两张图联系起来,无法进行全体像素对应,但是否能进行局部匹配?
A:肯定可以!!!
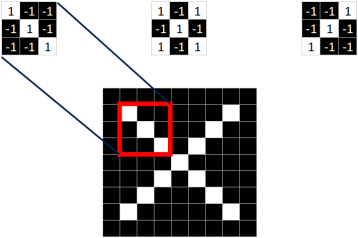
【4】从标准的X图中我们提取出三个特征(feature)
1号特征:
2号特征:
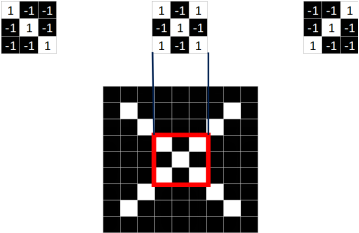
3号特征:
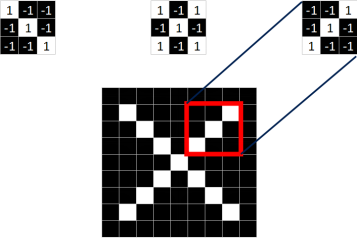
发现,只要用这三个feature,便可定位到X图片的某个局部
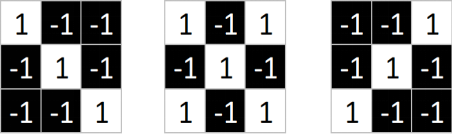
【5】这样的feature,在CNN中也被成为卷积核或者卷积单元(filter),一般是3X3,或者5X5的大小。而feature里的值,是通过模型学习得到的。
1.3 CNN中的二维卷积(Convolution2D)
卷积神经网络(CNN)包括一维卷积神经网络,二维卷积神经网络以及三维卷积神经网络。
一维卷积神经网络主要用于序列类的数据处理, 二维卷积神经网络常应用于图像类文本的识别, 三维卷积神经网络主要应用于医学图像以及视频类数据识别。
2D卷积是一个比较简单的操作:
(1)先从一个 3*3 的权重矩阵,也就是卷积核(filter)开始,让它逐步在二维输入数据上“扫描”。
(2)卷积核“滑动”的同时,计算权重矩阵和扫描所得的数据矩阵的乘积,然后把结果汇总成一个输出像素。
(3)卷积核会在它经过的所有位置上,都重复以上操作,直到把输入特征矩阵转换为另一个二维的特征矩阵。
动图的演示:
这是2D视角的动图:

这是3D视角的动图:
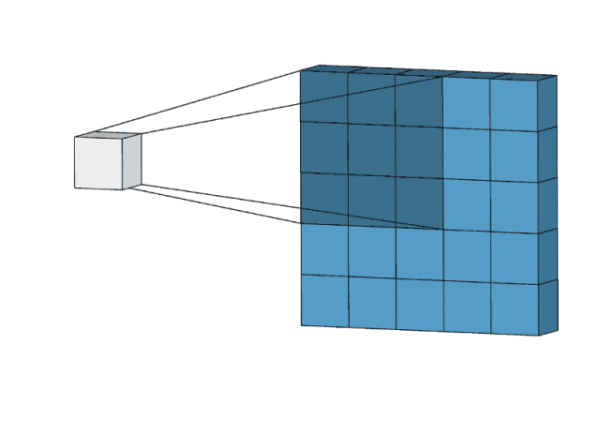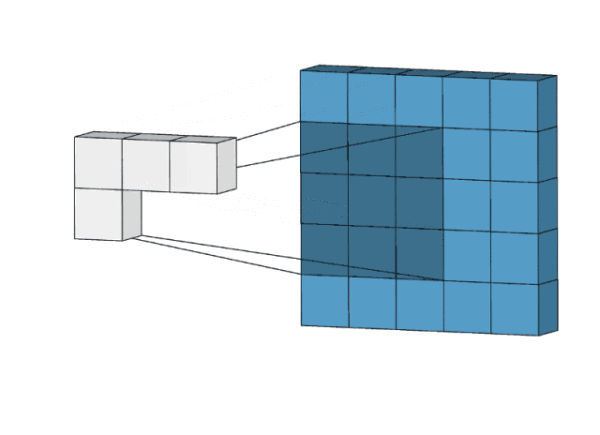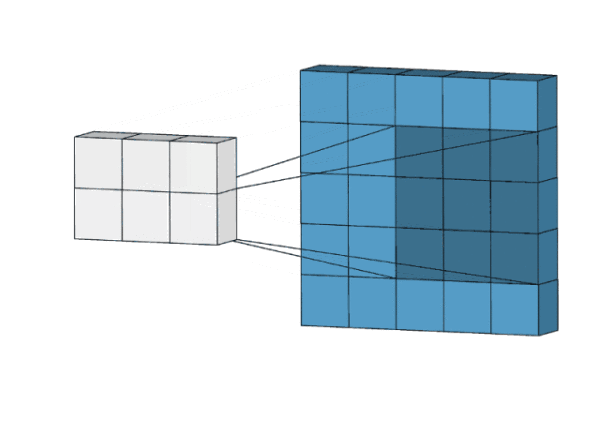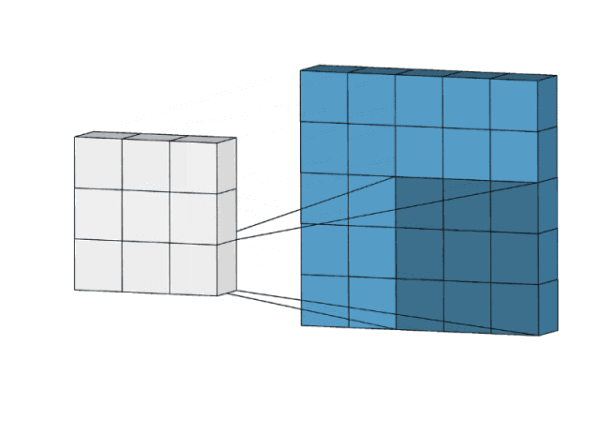
1.4 总结:
简而言之,输出的特征,基本上就是原输入特征的加权和(权重是卷积核自带的值),而从像素位置上看,它们所处的地方大致相同。
那么为什么输出特征,会落入这个“大致区域”呢?
这取决于卷积核的大小。 卷积核的大小直接决定了在生成输出特征时,它合并了多少输入特征,也就是说:卷积核越小,输入输出的位置越接近;卷积核越大,距离就越远。
这和全连接层很不一样。
在上图的例子中,我们的输入有5×5=25个特征,而我们的输出则是3×3=9个特征。
如果这是一个全连接层,输入25个特征后,我们会输出包含25×9=225个参数的权重矩阵,每个输出特征都是每个输入特征的加权和。
这意味着对于每个输入特征,卷积执行的操作是使用9个参数进行转换。
二、非线性激活层
CNN中非线性激活层通常使用relu函数,所以我们这里先介绍relu,再介绍其他的激活函数
2.1 什么是relu
官方解释:卷积层对原图运算多个卷积,产生一组线性激活响应,而非线性激活层是对之前的结果进行一个非线性的激活响应。
激活函数的作用是用来加入非线性因素,把卷积层输出结果做非线性映射。
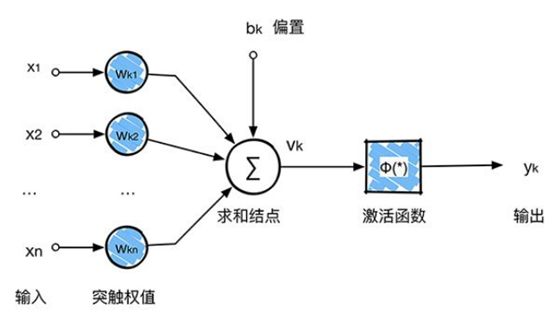
在卷积神经网络中用到最多的非线性激活函数是relu函数,
它的公式定义:f(x)=max(0,x)
即,保留大于等于0的值,其余所有小于0的数值直接改写为0
>=0的值全部保持不变:
而<0的值全部改写为0:
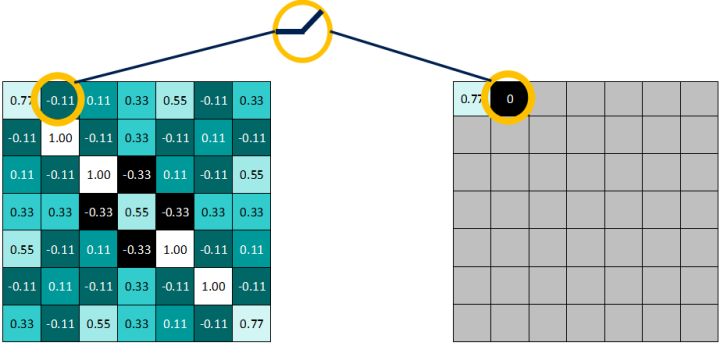
作用后的结果:
2.2 其他常见的非线性激活函数
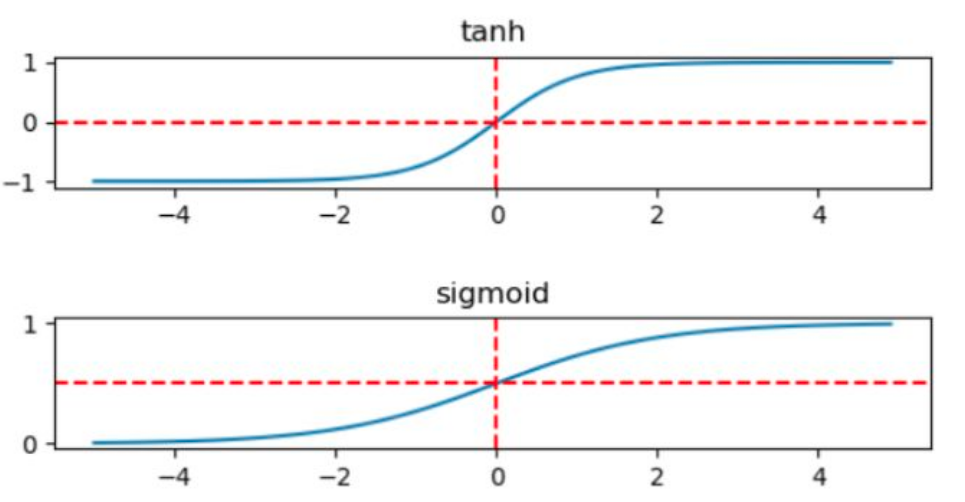
sigmoid函数:$sigmoid(x)=\frac{1}{1+e^{-x}} $
tanh函数: $tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
这两个函数的图像如下所示:
2.3 为何使用relu
实际应用中,特别是深层网络在训练时,tanh和sigmoid会在端值趋于饱和,造成训练速度减慢,故深层网络的激活函数默认大多采用relu函数,浅层网络可以采用sigmoid和tanh函数。
那么为什么现在这么多网络,都更多地使用relu函数呢?一个重要原因就是上面提到的,其稀疏激活性。
- 标准的sigmoid函数输出不具备稀疏性,需要用一些惩罚因子来训练出一大堆接近0的冗余数据来,从而产生稀疏数据
- 而relu是线性修正。它的作用是如果计算出的值小于0,就让它等于0,否则保持原来的值不变。
这是一种简单粗暴地强制某些数据为0的方法,然而经实践证明,训练后的网络完全具备适度的稀疏性。而且训练后的可视化效果和传统方式预训练出的效果很相似,这也说明了relu具备引导适度稀疏的能力。
因此,relu的使用,使得网络可以自行引入稀疏性,同时大大地提高了训练速度。
三、池化层pooling
3.1 池化的作用
池化操作,最大的作用就是减少数据量。池化层的引入,是仿照人的视觉系统对视觉输入对象进行降维和抽象。
在卷积神经网络过去的工作中,研究者普遍认为池化层有如下三个功效:
特征不变形:池化操作使得模型更加关注是否存在某些特征,而不是特征具体的位置。
特征降维:池化相当于在空间范围内做了维度约减,从而使模型可以抽取更加广范围的特征。同时减小了下一层的输入大小,进而减少计算量和参数个数。
在一定程度上防止过拟合,更方便优化。由1、2可知,这种池化机制能够有效地原因在于,在发现一个特征之后,它的精确位置远不及它和其他特征的相对位置的关系重要。池化层会不断地减小数据的空间大小,因此参数的数量和计算量也会下降,这在一定程度上也控制了过拟合。
3.2 池化的分类
池化分为两种,Max Pooling 最大池化、Average Pooling平均池化。
顾名思义,最大池化就是取最大值,平均池化就是取平均值。其中“最大池化(Max pooling)”最为常见。
当前最常用形式的池化层,是每隔2个元素从图像划分出2*2的区块,然后对每个区块中的4个数取最大值,这将会减少75%的数据量。
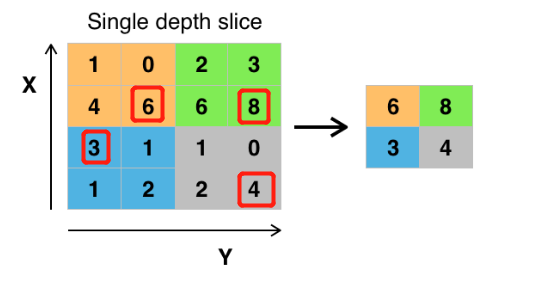
3.3 池化操作
通常,CNN的卷积层之间都会周期性地插入池化层
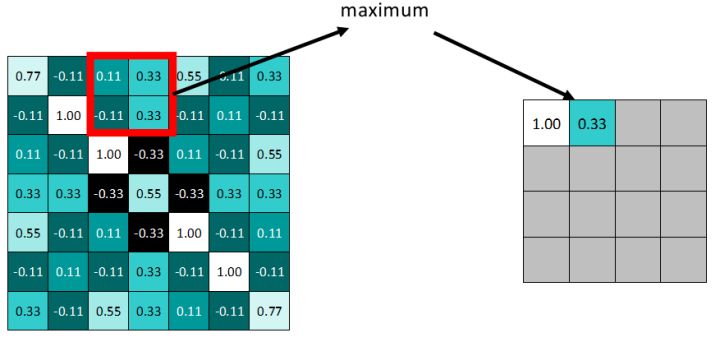
举例说明:
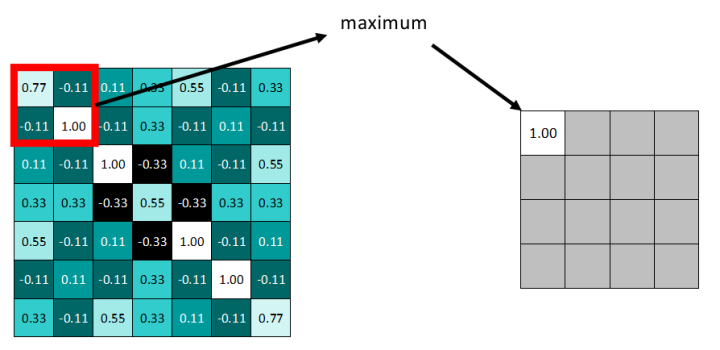
依据步长,滑动窗口
得到池化后的feature map,明显发现数据量减少了很多
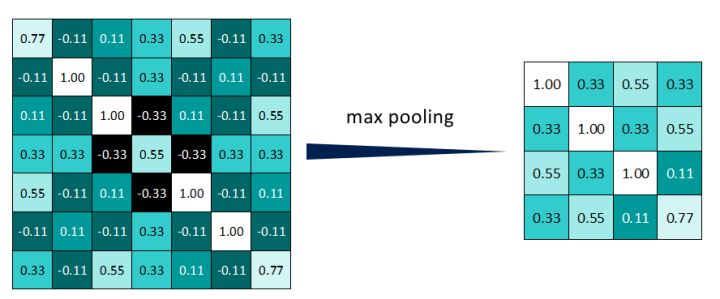
3.4 池化操作总结
因为最大池化保留了每一个小块内的最大值,所以它相当于保留了这一块最佳匹配结果。
这也就意味着:池化操作不会具体关注窗口内到底是哪一个地方匹配了,而只关注是不是有某个地方匹配上了。
侧面说明——CNN能够发现图像中是否具有某种特征,而不用在意到底在哪里具有这种特征。
这也就帮助解决,之前提到的计算机逐一像素匹配的死板做法。
四、全连接层
4.1 全连接层的作用
从侧面来理解
我们知道,局部连接与参数共享是卷积神经网络最重要的两个性质
局部连接?——回忆一下卷积层的操作,是用一个3X3的fliter与原图进行连接操作,很明显原图中只有一个3X3的窗口能够与fliter连接起来。
参数共享?——那窗口之外的、未连接的部分怎么办呢? 我们知道,采用的是将窗口滑动起来的方法后续进行连接。这个方法的思想就是“参数共享” ,参数指的就是filter,用滑动窗口的方式,将这个filter值共享给原图中的每一块区域,连接进行卷积运算。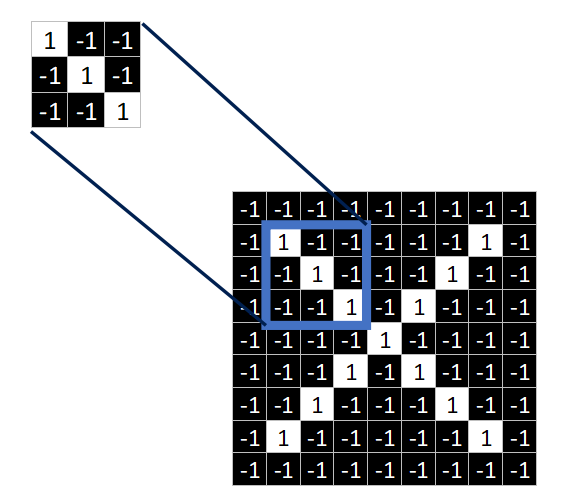
为什么是全连接?
卷积取的是局部特征,全连接就是把以前的局部特征重新通过权值矩阵,组装成完整的图,因为用到了所有的局部特征,所以叫全连接。
全连接层要做的,是什么?
起到“分类”的作用。
全连接层要做的,就是对之前的所有操作进行一个总结。对特征图进行维度上的改变,来得到每个分类类别对应的概率值。
4.2 全连接操作
接着上面的例子,原图片尺寸为9X9,在一系列的卷积、relu、池化操作后,得到尺寸被压缩为2X2的三张特征图。如下图所示:
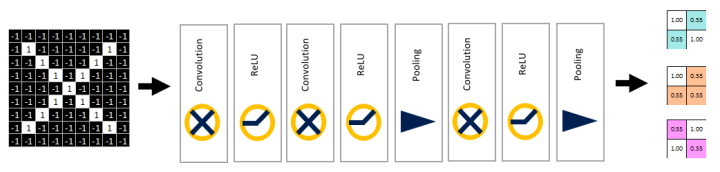
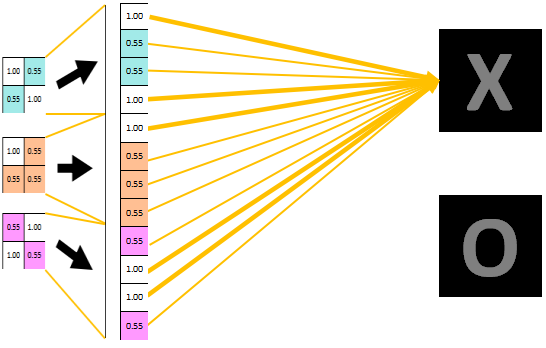
将三个特征图改变维度直接变成一维的数据,展开的数据即为属于类别X的概率值,值大小也在对应X的线条粗细中表现出来了。以上所有的操作都是对标准的原图X来进行的,因此最终分类显示即为X。
如果,对并不标准的图进行分类

进行一系列操作后,0.92表示极其大可能是X,因此对应到X的黄色线条比对应到O的绿色线条要粗很多很多
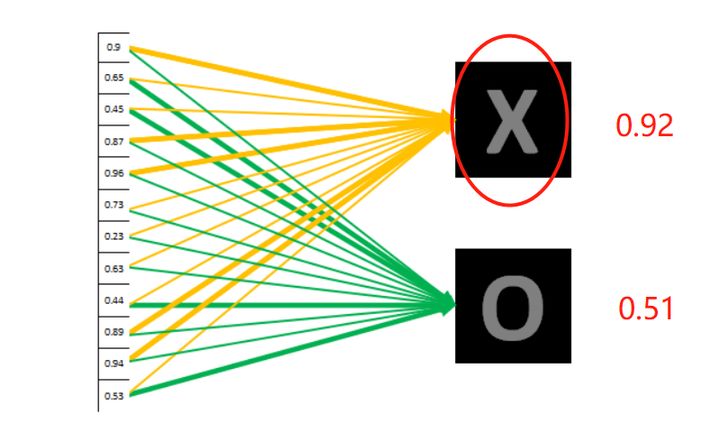
我们对结果进行统计分析后,可判断这张图片里的字母为X。
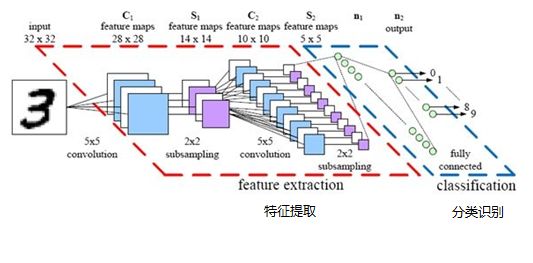
五、CNN总结
卷积神经网络主要由两部分组成,一部分是特征提取(卷积、激活函数、池化),另一部分是分类识别(全连接)