机器学习笔记（四）：手写多层神经网络并应用

在上一篇文章中，我们已经学习了多层神经网络的基本原理，并且对正向传播、反向传播和激活函数都有了一定的了解。

在这部分，我们将仅通过numpy和sklearn的accuracy_score（偷了个懒，没手写）来实现一个多层神经网络，并且将其应用到不同的情景中。

多层神经网络的构建

在理解了多层神经网络的原理之后，手写一个下面这样的代码并不是很难，所以这里就讲一讲主要的思路：

• 这里使用sigmoid函数作为激活函数；
• 根据上一篇文章介绍的神经网络的矩阵表示，我们这里直接用矩阵表示每一层的参数，并且将每一层的参数保存到一个列表中；
• 根据之前讲的正向传播、反向传播公式来构造正向传播、反向传播函数。
• 既然是使用矩阵表示神经网络，我们增加、减少层数都非常容易，所以我们可以通过初始化的时候传入参数来指定这个多层神经网络的结构，这样使用的时候就更灵活了。

需要注意的地方：

• 在手写实现的过程中我发现原始的sigmoid函数可能会溢出，所以就做了一点处理；

• 反向传播这里需要判断是输出层还是隐藏层，计算公式不一样；

• softmax函数仅仅用在predict函数中，目的是输出每一个种类的概率；

  这里的predict函数其实本质上就是正向传播，我为了方便处理数据才这么写的，实际上并不需要这么做。

import numpy as np
from sklearn.metrics import accuracy_score

# def sigmoid(x):
#     """
#     sigmoid函数
#     """
#     return 1.0 / (1 + np.exp(-x))

def sigmoid(Z):
    """
    sigmoid函数，解决了溢出的问题
    把大于0和小于0的元素分别处理
    原来的sigmoid函数是 1/(1+np.exp(-Z))
    当Z是比较小的负数时会出现上溢，此时可以通过计算exp(Z) / (1+exp(Z)) 来解决
    """
    mask = (Z > 0)
    positive_out = np.zeros_like(Z, dtype='float64')
    negative_out = np.zeros_like(Z, dtype='float64')

    # 大于0的情况
    positive_out = 1 / (1 + np.exp(-Z, positive_out, where=mask))
    # 清除对小于等于0元素的影响
    positive_out[~mask] = 0

    # 小于等于0的情况
    expZ = np.exp(Z, negative_out, where=~mask)
    negative_out = expZ / (1 + expZ)
    # 清除对大于0元素的影响
    negative_out[mask] = 0

    return positive_out + negative_out


# FIXME softmax函数输出的概率比较低，比如错误分类概率为0.18，而正确概率为0.22，相差不太大
def softmax(x):
    """
    对输入x的每一行计算softmax。
    该函数对于输入是向量（将向量视为单独的行）或者矩阵（M x N）均适用。
    代码利用softmax函数的性质: softmax(x) = softmax(x + c)
    :param x: 一个N维向量，或者M x N维numpy矩阵.
    """
    # 根据输入类型是矩阵还是向量分别计算softmax
    if len(x.shape) > 1:
        # 矩阵
        tmp = np.max(x, axis=1)  # 得到每行的最大值，用于缩放每行的元素，避免溢出。 shape为(x.shape[0],)
        x -= tmp.reshape((x.shape[0], 1))  # 利用性质缩放元素
        x = np.exp(x)  # 计算所有值的指数
        tmp = np.sum(x, axis=1)  # 每行求和
        x /= tmp.reshape((x.shape[0], 1))  # 求softmax
    else:
        # 向量
        tmp = np.max(x)  # 得到最大值
        x -= tmp  # 利用最大值缩放数据
        x = np.exp(x)  # 对所有元素求指数
        tmp = np.sum(x)  # 求元素和
        x /= tmp  # 求somftmax
    return x


class Neural_Network:
    """
    多层全连接神经网络
    """

    def __init__(self, nodes, rate=0.01, epoch=1000):
        """
        初始化一个神经网络实例
        :param nodes: 网络层次结构
        :param rate: 学习速率
        :param epoch: 最大迭代次数
        """
        # 网络层次结构
        self.nodes = nodes
        # 学习速率
        self.rate = rate
        # 最大迭代次数
        self.epoch = epoch

        # 偏置矩阵
        self.B = []
        # 权重矩阵
        self.W = []
        # 每一层的输出
        self.Z = []

        # 初始化权重与偏重
        for i in range(len(self.nodes) - 1):  # 对于每一层网络，根据该层节点数目进行初始化
            # 权重矩阵，不能初始化为0或1，不然迭代会失去梯度！
            w = np.random.randn(self.nodes[i], self.nodes[i + 1]) / np.sqrt(self.nodes[i])
            b = np.ones((1, self.nodes[i + 1]))
            self.W.append(w)
            self.B.append(b)

    def forward(self, data):
        """
        正向传播函数
        """
        # 存放每层输出
        Z = []
        x = data
        for j in range(len(self.nodes) - 1):
            x = sigmoid(x.dot(self.W[j]) + self.B[j])
            # 所有层输出存入list中
            Z.append(x)
        self.Z = Z

    def backpropagation(self, data, t):
        """
        反向传播函数
        """
        D = []
        d = t
        # 计算delta
        n_layer = len(self.nodes)
        for j in range(n_layer - 1, 0, -1):
            if j == n_layer - 1:  # 如果是输出层
                # delta = y * (1 - y) * (t - y)
                d = self.Z[-1] * (1 - self.Z[-1]) * (t - self.Z[-1])
            else:  # 如果是隐藏层
                # delta = y * (1-y) * sum( delta_k * w_k)
                d = self.Z[j - 1] * (1 - self.Z[j - 1]) * np.dot(d, self.W[j].T)
            # 存入list中，反向计算，后计算的存前面
            D.insert(0, d)

        # 更新权重和偏置
        # w += n * delta
        self.W[0] += self.rate * np.dot(data.T, D[0])
        self.B[0] += self.rate * np.sum(D[0], axis=0)
        for k in range(1, len(self.nodes) - 1):
            self.W[k] += self.rate * np.dot(self.Z[k - 1].T, D[k])
            self.B[k] += self.rate * np.sum(D[k], axis=0)

    def train(self, data, label, show_process=False):
        """
        进行训练
        :param data: 训练集数据
        :param label: 训练集标签
        :param show_process: 是否展示迭代过程
        """
        # 根据样本个数创建正确结果矩阵，每个样本对应结果矩阵中正确的结果位置值1，其他置0
        t = np.zeros((np.shape(data)[0], self.nodes[-1]))
        for i in range(self.nodes[-1]):
            t[np.where(label == i), i] = 1

        for i in range(self.epoch):
            self.forward(data)

            if show_process:
                loss = np.sum((t - self.Z[-1]) ** 2)
                predict = np.argmax(self.Z[-1], axis=1)
                accuracy = accuracy_score(label, predict)
                print("Loss:%f" % loss, end=' ')
                print("accuracy%f" % accuracy)

            self.backpropagation(data, t)

    def predict(self, data, display=False):
        """
        进行预测，通过softmax给出最后的预测结果和类别所属的概率
        :param data: 预测数据
        :param display: 是否展示softmax的结果
        :return: 预测结果和预测概率
        """
        # 存放每层输出
        Z = []
        x = data
        for j in range(len(self.nodes) - 1):
            x = sigmoid(x.dot(self.W[j]) + self.B[j])
            # 所有层输出存入list中
            Z.append(x)
        softmax_result = softmax(Z[-1])
        result = np.argmax(softmax_result, axis=1)
        rate = []
        for i in range(len(result)):
            rate.append(softmax_result[i, result[i]])
        if display:
            print(softmax_result)
        return result, rate

解决circles问题

这里使用的是和机器学习笔记（一）：K-Means聚类算法一样的数据集，获取方式参考这篇文章即可。

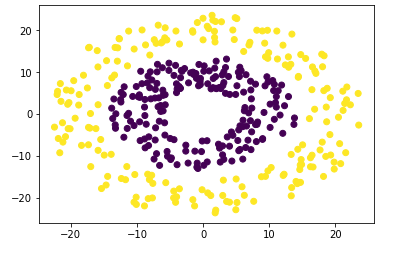
定义Neural Network实例时我们传入了参数nodes=[2, 8, 8, 2]，因为

• 数据集是两个平面上的圆环，所以每个点的坐标都可以用两个数表示，从而输入层节点为2；
• 我们定义中间有两个隐藏层，每个隐藏层有8个节点；
• 我们需要预测某个点是属于哪个圆环上的，只有两种圆环，所以是一个二分类问题，因此输出层节点为2。

import time
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import accuracy_score

import sklearn.neural_network as NN
import Neural_Network as MyNN

fig_num = 0


def plotFeature(data, labels_):
    """
    二维空间显示聚类结果
    """
    # 获取簇集的个数
    clusterNum = len(set(labels_))
    # 内定的颜色种类
    scatterColors = ["orange", "purple", "cyan", "red", "green"]

    # 判断数据的维度是不是２
    if np.shape(data)[1] != 2:
        print("sorry,the dimension of your dataset is not 2!")
        return 1
    # 判断簇集类别是否大于５类
    if clusterNum > len(scatterColors):
        print("sorry,your k is too large,please add length of the scatterColors!")
        return 1

    # 散点图的绘制
    for i in range(clusterNum):
        colorSytle = scatterColors[i % len(scatterColors)]
        subCluster = data[np.where(labels_ == i)]
        plt.scatter(subCluster[:, 0], subCluster[:, 1], c=colorSytle, s=20)

    # 设置x、y轴和标题
    plt.xlabel("x-label")
    plt.ylabel("y-label")
    plt.show()


def load_circles(rate=0.7):
    # 从文本中加载数据
    dataset_circles = np.loadtxt("../dataset_circles.csv", delimiter=",")
    # 随机打乱数据
    data_size = np.shape(dataset_circles)[0]
    shuffled_index = np.random.permutation(data_size)
    dataset_circles = dataset_circles[shuffled_index]
    # 分割前两列为data
    data = dataset_circles.T[0:2]
    # 分割第三列为label
    label = dataset_circles.T[2:3]
    # 分割数据集
    split_index = int(data_size * rate)
    train_data = data.T[:split_index]
    train_label = label.T[:split_index]
    test_data = data.T[split_index:]
    test_label = label.T[split_index:]
    return train_data, train_label, test_data, test_label


if __name__ == "__main__":
    train_data, train_label, test_data, test_label = load_circles(rate=0.75)
    # =====================使用自己的方法做预测========================
    # 构建一个多层神经网络
    nn = MyNN.Neural_Network(nodes=[2, 8, 8, 2], rate=0.01, epoch=2000)

    # 开始训练并且计时
    start = time.clock()
    nn.train(train_data, train_label, show_process=False)
    end = time.clock()
    print("MyNN 训练用时:\t%f s" % (end - start))

    # 对训练集做预测并且输出准确度与结果
    train_result, _ = nn.predict(train_data)
    print("MyNN 对训练集做预测:\t", accuracy_score(train_label, train_result))
    plotFeature(train_data, train_result)

    # 对测试集做预测并且输出准确度与结果
    test_result, _ = nn.predict(test_data)
    print("MyNN 对测试集做预测:\t", accuracy_score(test_label, test_result))
    plotFeature(test_data, test_result)
    # =====================使用sklearn做预测========================
    # 构建一个多层神经网络
    # 因为这里使用的数据量很少，根据网上的介绍，使用lbfgs方法来优化权重，收敛更快效果也更好
    clf = NN.MLPClassifier(solver='lbfgs', activation='logistic', max_iter=300, alpha=1e-5, hidden_layer_sizes=(30, 30))
    # 开始训练并且计时
    start = time.clock()
    clf.fit(train_data, train_label)
    end = time.clock()
    print("sklearn 训练用时:\t%f s" % (end - start))

    # 对训练集做预测并且输出准确度与结果
    train_result = clf.predict(train_data)
    print("sklearn 对训练集做预测:\t", accuracy_score(train_label, train_result))
    plotFeature(train_data, train_result)

    # 对测试集做预测并且输出准确度与结果
    test_result = clf.predict(test_data)
    print("sklearn 对测试集做预测:\t", accuracy_score(test_label, test_result))
    plotFeature(test_data, test_result)

解决moons问题

这里我们使用的是sklearn的moons数据集，通过sklearn.datasets.make_moons函数就可以创建一个指定规模和噪声的数据集。

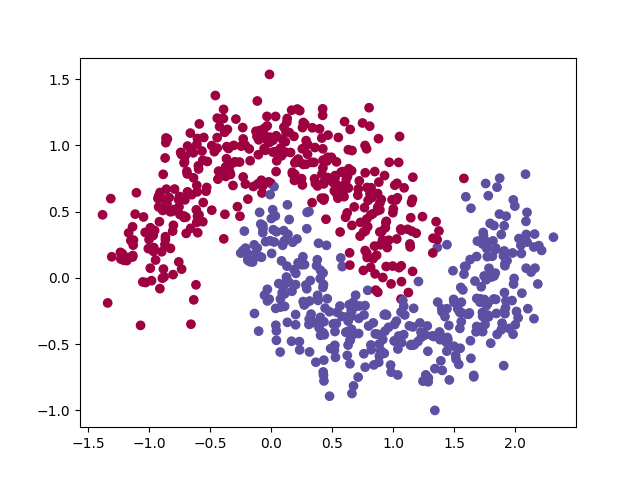
这个数据集本质上和circles没有区别，都是二分类问题，所以代码基本上和上面一样。

不过因为之前的circles可以通过特征变换，变成点到原点的距离，然后采用KMeans可以得到一个比较好的效果；而这里的moons并不是很好处理，直接采用KMeans算法可能效果并不是很好。

import time
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score

import sklearn.neural_network as NN
import Neural_Network as MyNN


def load_moons(size=200, rate=0.7, noise=0.20):
    # generate sample data
    np.random.seed(0)
    data, label = datasets.make_moons(size, noise=noise)
    # 随机打乱数据
    shuffled_index = np.random.permutation(size)
    data = data[shuffled_index]
    label = label[shuffled_index]
    # 分割数据集
    split_index = int(size * rate)
    train_data = data[:split_index]
    train_label = label[:split_index]
    test_data = data[split_index:]
    test_label = label[split_index:]
    return train_data, train_label, test_data, test_label


def plotFeature(data, label):
    plt.scatter(data[:, 0], data[:, 1], c=label, cmap=plt.cm.Spectral)
    plt.show()


if __name__ == "__main__":
    train_data, train_label, test_data, test_label = load_moons(size=1000, rate=0.75, noise=0.20)
    # =====================使用自己的方法做预测========================
    # 构建一个多层神经网络
    nn = MyNN.Neural_Network(nodes=[2, 8, 8, 2], rate=0.01, epoch=1000)

    # 开始训练并且计时
    start = time.clock()
    nn.train(train_data, train_label, show_process=False)
    end = time.clock()
    print("MyNN 训练用时:\t%f s" % (end - start))

    # 对训练集做预测并且输出准确度与结果
    train_result, _ = nn.predict(train_data)
    print("MyNN 对训练集做预测:\t", accuracy_score(train_label, train_result))
    plotFeature(train_data, train_result)

    # 对测试集做预测并且输出准确度与结果
    test_result, _ = nn.predict(test_data)
    print("MyNN 对测试集做预测:\t", accuracy_score(test_label, test_result))
    plotFeature(test_data, test_result)
    # =====================使用sklearn做预测========================
    # 构建一个多层神经网络
    # 因为这里使用的数据量很少，根据网上的介绍，使用lbfgs方法来优化权重，收敛更快效果也更好
    clf = NN.MLPClassifier(solver='lbfgs', activation='logistic', max_iter=300, alpha=1e-5, hidden_layer_sizes=(16, 16))
    # 开始训练并且计时
    start = time.clock()
    clf.fit(train_data, train_label)
    end = time.clock()
    print("sklearn 训练用时:\t%f s" % (end - start))

    # 对训练集做预测并且输出准确度与结果
    train_result = clf.predict(train_data)
    print("sklearn 对训练集做预测:\t", accuracy_score(train_label, train_result))
    plotFeature(train_data, train_result)

    # 对测试集做预测并且输出准确度与结果
    test_result = clf.predict(test_data)
    print("sklearn 对测试集做预测:\t", accuracy_score(test_label, test_result))
    plotFeature(test_data, test_result)

解决手写数字识别问题

这里使用的是和机器学习（二）：逻辑回归算法一样的数据集。

手写数字识别比上面两个要稍微复杂一点，我们先分析手写数字识别的特征：

• 每一张图片是8*8大小的，但这里我们定义的全连接神经网络不支持输入矩阵，所以我们需要把每一张图片变成向量，这样输入层节点数目就应该是64；
• 我们需要区分0~9这10个手写数字，所以这是一个多分类问题，输出层的节点数目应该是10。

确定了输入输出，我们就可以很容易的定义一个多层神经网络来处理这个问题了。

这部分定义Neural Network实例时我们传入的参数nodes=[64, 64, 32, 10]。

import time
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_digits
from sklearn.metrics import confusion_matrix, accuracy_score

import sklearn.neural_network as NN
import Neural_Network as MyNN

fig_num = 0


def display(images, ground_truth, predict, rate, fig_name):
    """
    画出预测结果
    :param images: 数字的图片
    :param ground_truth: 真值
    :param predict: 预测值
    :param fig_name: 图片名字
    """
    # plot the digits
    global fig_num
    fig_num += 1
    if fig_name is None:
        fig = plt.figure(fig_num, figsize=(6, 6))  # figure size in inches
    else:
        fig = plt.figure(fig_name, figsize=(6, 6))  # figure size in inches
    fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
    size = np.shape(predict)[0]
    if size > 56:
        size = 56
    # plot the digits: each image is 8x8 pixels
    for i in range(size):
        ax = fig.add_subplot(8, 8, i + 1, xticks=[], yticks=[])
        ax.imshow(images[i], cmap=plt.cm.binary)
        # label the image with the target value
        ax.text(0, 7, str(ground_truth[i]))
        if int(ground_truth[i]) == int(predict[i]):
            ax.text(6, 7, str(int(predict[i])), color='green', size=15)
            if rate is not None:
                ax.text(4, 1, str(int(rate[i] * 100) / 100), color='green', size=10)
        else:
            ax.text(6, 7, str(int(predict[i])), color='red', size=20)
            if rate is not None:
                ax.text(4, 1, str(int(rate[i] * 100) / 100), color='red', size=10)

    # plot confusion matrix
    cm = confusion_matrix(ground_truth, predict)
    plt.matshow(cm)
    plt.colorbar()
    plt.title(fig_name + ' ' + 'Confusion Matrix')
    plt.ylabel('Groundtruth')
    plt.xlabel('Predict')


def load_data(train_size=0.75):
    """
    加载数据同时分割出训练集和测试集
    :param train_size: 训练集的比例
    :return 分割好的数据集
    """
    # 加载数据
    # 这个函数返回的应该是一个类实例，里面有很多的变量，需要“单独的拿出来用”
    digits = load_digits()
    # 输出查看一下这个类的属性和方法
    # print(dir(digits))
    # 获得数据的大小
    data_size = np.shape(digits.data)[0]
    # 将数据打乱，这里需要把这个类的要用上的变量都对应上，有点麻烦（是否有更简便的方法？）
    shuffled_index = np.random.permutation(data_size)

    digits.data = digits.data[shuffled_index]
    digits.images = digits.images[shuffled_index]
    digits.target = digits.target[shuffled_index]

    # 分割数据集
    split_index = int(data_size * train_size)

    train_data = digits.data[0:split_index]
    train_target = digits.target[0:split_index]
    train_images = digits.images[0:split_index]

    test_data = digits.data[split_index:]
    test_target = digits.target[split_index:]
    test_images = digits.images[split_index:]

    return train_data, train_target, train_images, test_data, test_target, test_images


if __name__ == "__main__":
    # FIXME:
    #  1. 数据的加载应该没问题，在逻辑回归里面得到的结果是正确的
    #  但放到神经网络里面，如果给的训练集过多（1000以上），就没有收敛，但给的数据集少一些效果好一些
    #  2. 感觉是有地方溢出了，导致直接就没有收敛，猜测是sigmoid函数溢出
    #  3. 测试发现sigmoid函数没有溢出，可能是学习率过低，陷入了局部最优解，但调大学习率就会报警，说sigmoid函数溢出
    #  4. 调整sigmoid函数后，调大学习率没有影响，但把学习率调小会得到一个很好的结果。
    #  问题：如何获得最优的学习率？如何知道学习率是过大还是过小？
    # 加载并且分割各种数据
    train_data, train_target, train_images, test_data, test_target, test_images = load_data(train_size=0.75)
    # =====================使用自己的方法做预测========================
    nn = MyNN.Neural_Network(nodes=[64, 64, 32, 10], rate=0.001, epoch=1000)

    # 开始训练并且计时
    # FIXME 这里时间测量的不对，但其他地方没有问题
    start = time.clock()
    nn.train(train_data, train_target, show_process=True)
    end = time.clock()
    print("MyNN 训练用时:\t%f s" % (end - start))

    # 对训练集做预测并且输出准确度与结果
    train_result, train_rate = nn.predict(train_data)
    print("MyNN 对训练集做预测:\t", accuracy_score(train_target, train_result))
    display(train_images, train_target, train_result, train_rate, "My Train")

    # 对测试集做预测并且输出准确度与结果
    test_result, test_rate = nn.predict(test_data)
    print("MyNN 对测试集做预测:\t", accuracy_score(test_target, test_result))
    display(test_images, test_target, test_result, test_rate, "My Test")
    # =====================使用sklearn做预测========================
    # 构建一个多层神经网络
    # 因为这里使用的数据量很少，根据网上的介绍，使用lbfgs方法来优化权重，收敛更快效果也更好
    clf = NN.MLPClassifier(solver='lbfgs', activation='logistic', max_iter=300, alpha=1e-5, hidden_layer_sizes=(64, 64))
    # 开始训练并且计时
    start = time.clock()
    clf.fit(train_data, train_target)
    end = time.clock()
    print("sklearn 训练用时:\t%f s" % (end - start))

    # 对训练集做预测并且输出准确度与结果
    train_result = clf.predict(train_data)
    print("sklearn 对训练集做预测:\t", accuracy_score(train_target, train_result))
    display(train_images, train_target, train_result, None, "sklearn Train")

    # 对测试集做预测并且输出准确度与结果
    test_result = clf.predict(test_data)
    print("sklearn 对测试集做预测:\t", accuracy_score(test_target, test_result))
    display(test_images, test_target, test_result, None, "sklearn Test")

    plt.show()