机器学习笔记（二）：逻辑回归算法

机器学习（二）：逻辑回归算法

逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上，套用了一个逻辑函数，但也就由于这个逻辑函数，使得逻辑回归模型能够输出类别的概率。

逻辑回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。

1. 什么是回归

一说回归最先想到的是终结者那句：I’ll be back

regress，re表示back，gress等于go，数值go back to mean value，也就是I’ll be back 的意思

在数理统计中，回归是确定多种变量相互依赖的定量关系的方法

通俗理解：越来越接近期望值的过程，回归 于事物的本质

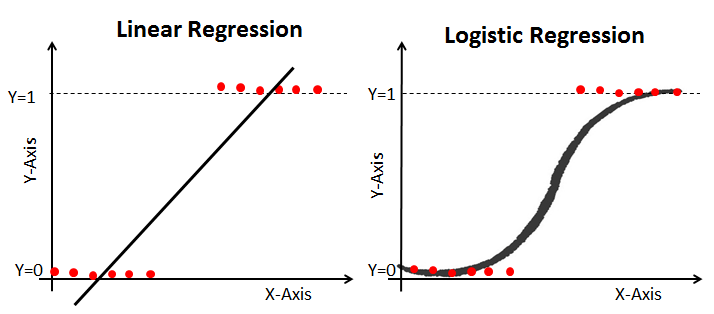
最简单的回归是线性回归(Linear Regression)，也就是通过最小二乘等方法得到模型的参数。线性回归假设输出变量是若干输出变量的线性组合，并根据这一关系求解线性组合中的最优系数。

通俗理解：输出一个线性函数，例如$y=f(x; \theta)$，通过寻找最优的参数$\theta$使得观测数据与模型数据相吻合。

2. 逻辑回归模型

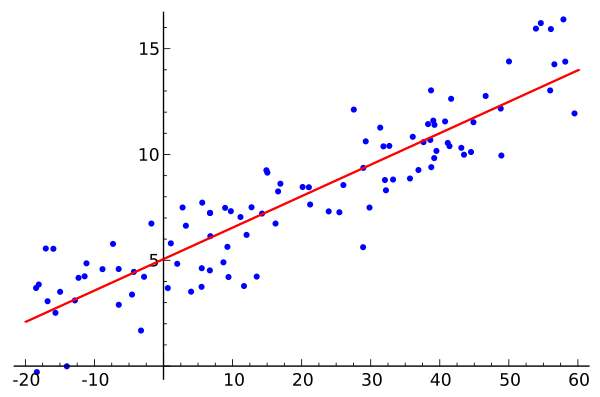
回归是一种比较容易理解的模型，就相当于$y=f(x)$，表明自变量$x$与因变量$y$的关系。

以常见的看医举例，医生治病时的望、闻、问、切，之后判定病人是否生病或生了什么病，其中的望闻问切就是获取自变量$x$，即特征数据，判断是否生病就相当于获取因变量$y$，即预测分类。

$X$为数据点——肿瘤的大小，$Y$为观测值——是否是恶性肿瘤。

通过构建线性回归模型，如$h_\theta(x)$所示，构建线性回归模型后，即可以根据肿瘤大小，预测是否为恶性肿瘤$h_\theta(x)) \ge 0.5$为恶性，$h_\theta(x) \lt 0.5$为良性。

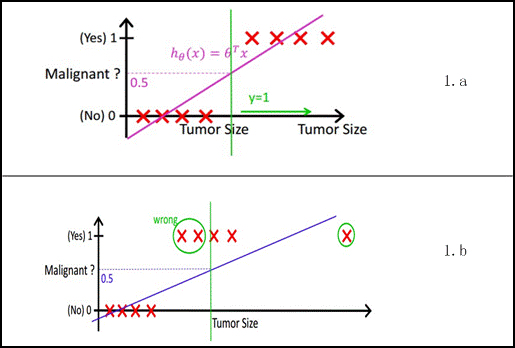
然而线性回归的鲁棒性很差，例如在上图的数据集上建立回归，因最右边噪点的存在，使回归模型在训练集上表现都很差。这主要是由于线性回归在整个实数域内敏感度一致，而分类范围，需要在$[0,1]$。

逻辑回归就是一种减小预测范围，将预测值限定为$[0,1]$间的一种回归模型，其回归方程与回归曲线如下图所示。逻辑曲线在$z=0$时，十分敏感，在$z>>0$或$z<<0$处，都不敏感，将预测值限定为$(0,1)$。

2.1 逻辑回归表达式

这个函数称为Logistic函数(Logistic Function)，也称为Sigmoid函数(Sigmoid Function)。函数公式如下：

$$
g(z) = \frac{1}{1+e^{-z}}
$$

Logistic函数:

• 当$z$趋近于无穷大时，$g(z)$趋近于1；
• 当$z$趋近于无穷小时，$g(z)$趋近于0。

Logistic函数的图形如上图所示。Logistic函数求导时有一个特性，这个特性将在下面的推导中用到，这个特性为：
$$
g’(z) = \frac{d}{dz} \frac{1}{1+e^{-z}} \
= \frac{1}{(1+e^{-z})^2}(e^{-z}) \
= \frac{1}{(1+e^{-z})} (1 - \frac{1}{(1+e^{-z})}) \
= g(z)(1-g(z))
$$
逻辑回归本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数$g(z)$将做为假设函数来预测。

$g(z)$可以将连续值映射到0到1之间。线性回归模型的表达式带入$g(z)$，就得到逻辑回归的表达式:
$$
h_\theta(x) = g(\theta^T x) = \frac{1}{1+e^{-\theta^T x}}
$$

2.2 逻辑回归的软分类

现在我们将y的取值$h_\theta(x)$通过Logistic函数归一化到(0,1)间，$y$的取值有特殊的含义，它表示结果取1的概率，因此对于输入$x$分类结果为类别1和类别0的概率分别为：

$$
P(y=1|x,\theta) = h_\theta(x) \
P(y=0|x,\theta) = 1 - h_\theta(x)
$$

对上面的表达式合并一下就是：

$$
p(y|x,\theta) = (h_\theta(x))^y (1 - h_\theta(x))^{1-y}
$$

2.3 梯度上升

得到了逻辑回归的表达式，下一步跟线性回归类似，构建似然函数，然后最大似然估计，最终推导出$\theta$的迭代更新表达式。只不过这里用的不是梯度下降，而是梯度上升，因为这里是最大化似然函数。

假设训练样本相互独立，那么似然函数表达式为：

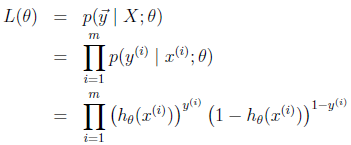
同样对似然函数取log，转换为：

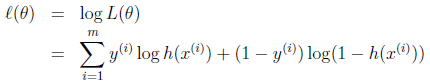
转换后的似然函数对$\theta$求偏导，在这里我们以只有一个训练样本的情况为例：

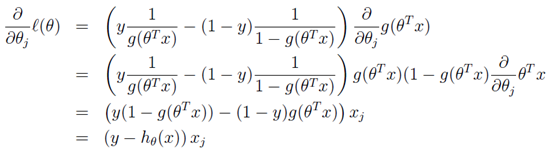
这个求偏导过程中：

• 第一步是对$\theta$偏导的转化，依据偏导公式：$y=lnx$, $y’=1/x$。
• 第二步是根据$g(z)$求导的特性$g’(z) = g(z)(1 - g(z))$ 。
• 第三步就是普通的变换。

这样我们就得到了梯度上升每次迭代的更新方向，那么$\theta$的迭代表达式为：
$$
\theta = \theta + \eta (y^i - h_\theta(x^i)) x_j^i
$$

其中$\eta$是学习速率。

3. 手写逻辑回归

这里以手写数字识别为例。我们手写一个逻辑回归类处理这个多分类问题，同时使用sklearn的逻辑回归模型作对比。

import random
import time
import matplotlib.pyplot as plt
import numpy as np
from math import inf
from sklearn.datasets import load_digits
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix


def sigmoid(x):
    """
    sigmoid函数
    """
    return 1.0 / (1 + np.exp(-x))


def acc_score(predict_data, raw_data):
    """
    计算结果的准确率
    :param predict_data: 预测值
    :param raw_data: 真值
    """
    cnt = 0
    size = np.shape(predict_data)[0]
    for i in range(size):
        if int(raw_data[i]) == int(predict_data[i]):
            cnt += 1
    score = float(cnt / size)
    return score


fig_num = 0


def display(images, ground_truth, predict, fig_name):
    """
    画出预测结果
    :param images: 数字的图片
    :param ground_truth: 真值
    :param predict: 预测值
    :param fig_name: 图片名字
    """
    # plot the digits
    global fig_num
    fig_num += 1
    if fig_name is None:
        fig = plt.figure(fig_num, figsize=(6, 6))  # figure size in inches
    else:
        fig = plt.figure(fig_name, figsize=(6, 6))  # figure size in inches
    fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
    size = np.shape(predict)[0]
    if size > 56:
        size = 56
    # plot the digits: each image is 8x8 pixels
    for i in range(size):
        ax = fig.add_subplot(8, 8, i + 1, xticks=[], yticks=[])
        ax.imshow(images[i], cmap=plt.cm.binary)
        # label the image with the target value
        ax.text(0, 7, str(ground_truth[i]))
        if int(ground_truth[i]) == int(predict[i]):
            ax.text(6, 7, str(int(predict[i])), color='green', size=15)
        else:
            ax.text(6, 7, str(int(predict[i])), color='red', size=20)

    # plot confusion matrix
    cm = confusion_matrix(ground_truth, predict)
    plt.matshow(cm)
    plt.colorbar()
    plt.title(fig_name + ' ' + 'Confusion Matrix')
    plt.ylabel('Groundtruth')
    plt.xlabel('Predict')


def load_data(train_size=0.75):
    """
    加载数据同时分割出训练集和测试集
    :param train_size: 训练集的比例
    :return 分割好的数据集
    """
    # 加载数据
    # 这个函数返回的应该是一个类实例，里面有很多的变量，需要“单独的拿出来用”
    digits = load_digits()
    # 输出查看一下这个类的属性和方法
    # print(dir(digits))
    # 获得数据的大小
    data_size = np.shape(digits.data)[0]
    # 将数据打乱，这里需要把这个类的要用上的变量都对应上，有点麻烦（是否有更简便的方法？）
    shuffled_index = np.random.permutation(data_size)

    digits.data = digits.data[shuffled_index]
    digits.images = digits.images[shuffled_index]
    digits.target = digits.target[shuffled_index]

    # 分割数据集
    split_index = int(data_size * train_size)

    train_data = digits.data[0:split_index]
    train_target = digits.target[0:split_index]
    train_images = digits.images[0:split_index]

    test_data = digits.data[split_index:]
    test_target = digits.target[split_index:]
    test_images = digits.images[split_index:]

    return train_data, train_target, train_images, test_data, test_target, test_images


class Logistic_Regression:
    """
    逻辑回归模型，通过OVR(One-Vs-All)解决多分类问题
    """

    def __init__(self, data, label, max_iter=500, alpha=0.01, tol=0.000005):
        """
        初始化逻辑回归类
        :param data: 加载训练集
        :param label: 加载训练集的标签
        :param max_iter: 最大迭代次数
        :param alpha: 学习率（步长）
        :param tol: 停止求解的标准，当收敛速度过慢时停止求解
        """
        # 保存传入数据
        self.data = data
        self.label = label
        self.max_iter = max_iter
        self.alpha = alpha
        self.tol = tol

        # 进一步处理
        # 数据长度m与单个数据的长度n
        self.m, self.n = np.shape(data)
        # 数据权重
        self.weights = np.ones((10, self.n))
        # 常数项
        self.b = np.ones(10)

    def train(self, method="SGD"):
        """
        进行训练，这里采用的是OVR方法解决多分类问题
        :param method: 使用的求解方法
        """
        # 对于每一个数字
        for number in range(10):
            # 重新打标签
            label = np.copy(self.label)
            for i in range(self.m):
                if label[i] == number:
                    label[i] = 1
                else:
                    label[i] = 0
            if method == "SGD":
                # 采用随机梯度上升法进行迭代求解
                self.SGD(number, label)
            elif method == "MBGD":
                # 采用小批量梯度下降法
                self.MBGD(number, label)
            else:
                print("error method:", method)
                exit(-1)

    def predict(self, predict_data):
        """
        进行预测
        :param predict_data: 测试集
        """
        # 保存对测试集的预测结果
        result = np.zeros(np.shape(predict_data)[0])
        # 保存对单个数据，每个分类器给出的结果
        ans = np.zeros(10)
        # 开始对整个测试集进行预测
        for i in range(len(result)):
            # 分别用每个数字的分类器进行预测
            for k in range(10):
                ans[k] = sigmoid(sum(self.weights[k, :] * predict_data[i, :] + self.b[k]))
            ans = list(ans)
            result[i] = ans.index(max(ans))
        return result

    def SGD(self, number, label):
        """
        使用老师上课讲的随机梯度上升法求解
        :param number: 目前需要被分类的数字
        :param label: 根据这个数组制作的标签
        """
        for i in range(self.max_iter):
            # 上次的误差
            last_error = inf
            num_index = list(range(self.m))
            for j in range(self.m):
                # FIXME
                #  之前其实是随机打乱了的，所以这里是不是没有必要进行这样的操作？
                #  这里实际上还是用上了所有的样本，所以实际上这里随机取值对结果并没有影响
                rand_index = int(np.random.uniform(0, len(num_index)))
                error = label[rand_index] - sigmoid(
                    sum(self.weights[number] * train_data[rand_index]) + self.b[number])
                # 实际上下面这样做的效果不好，error可能为正也可能为负。。。
                # if abs(error) > abs(last_error):
                # if error > last_error:
                #     continue
                # 下面右边应该是 学习率*(1-g(z))*z，是求偏导的过程
                self.weights[number] += self.alpha * error * train_data[rand_index]
                self.b[number] += self.alpha * error
                del (num_index[rand_index])
                if abs(last_error - error) < self.tol:
                    break
                last_error = error

    def MBGD(self, number, label):
        """
        尝试使用小批量梯度下降法求解
        :param number: 目前需要被分类的数字
        :param label: 根据这个数组制作的标签
        """
        for i in range(self.max_iter):
            # 上次的误差
            last_error = inf
            # 小批量的数目
            if self.m < 200:
                m = random.randint(1, self.m)
            else:
                m = random.randint(10, 200)
            num_index = list(range(self.m))
            for j in range(m):
                rand_index = int(np.random.uniform(0, len(num_index)))
                error = label[rand_index] - sigmoid(
                    sum(self.weights[number] * train_data[rand_index]) + self.b[number])
                self.weights[number] += self.alpha * error * train_data[rand_index]
                self.b[number] += self.alpha * error
                del (num_index[rand_index])
                if abs(last_error - error) < self.tol:
                    break
                last_error = error


if __name__ == "__main__":
    # 加载并且分割各种数据
    train_data, train_target, train_images, test_data, test_target, test_images = load_data(train_size=0.75)

    # =====================使用自己的方法做预测========================
    # 生成一个逻辑回归类实例，并且把训练集导入
    lr = Logistic_Regression(train_data, train_target, 3000, 0.01, 0.0000005)
    # 开始训练并且计时
    start = time.clock()
    lr.train(method="SGD")
    end = time.clock()
    print("训练用时:\t%f s" % (end - start))
    # 对训练集做预测并且输出准确度与结果
    train_result = lr.predict(train_data)
    print("对训练集做预测:\t", acc_score(train_result, train_target))
    display(train_images, train_target, train_result, "My Train")
    # 对测试集做预测并且输出准确度与结果
    test_result = lr.predict(test_data)
    print("对测试集做预测:\t", acc_score(test_result, test_target))
    display(test_images, test_target, test_result, "My Test")

    # =====================使用sklearn做预测========================
    skl = LogisticRegression()

    start = time.clock()
    skl.fit(train_data, train_target)
    end = time.clock()
    print("训练用时:\t%f s" % (end - start))

    pred_train = skl.predict(train_data)
    print("对训练集做预测:\t", acc_score(pred_train, train_target))
    display(train_images, train_target, pred_train, "Sklearn Train")

    pred_test = skl.predict(test_data)
    print("对测试集做预测:\t", acc_score(pred_test, test_target))
    display(test_images, test_target, pred_test, "Sklearn Test")

    plt.show()

手写逻辑回归预测结果展示：