机器学习笔记（一）：K-Means聚类算法

K-Means 机器学习
机器学习
发布日期:   2022-01-07
文章字数:   2.3k
阅读时长:   9 分
阅读次数:  

机器学习笔记（一）：K-Means聚类算法

2021年下半年选修了两门机器学习相关的课程，感觉学到了非常多的知识，打算好好整理一下。

大部分内容是从课件里面搬运来的，但大部分代码是自己理解的基础上写出来的。

根据训练样本中是否包含标签信息，机器学习可以分为 监督学习 和 无监督学习。

聚类算法是典型的无监督学习，其训练的样本中值包含样本的特征，不包含样本的标签信息。在聚类算法中，利用样本的特征，将具有相似特征空间分布的样本划分到同一类别中。

1. 算法原理

由于具有出色的速度和良好的可扩展性，K-Means聚类算法是最经典的聚类方法。

k-Means算法是一个重复移动类中心点（重心，centroids）的过程:

  • 移动中心点到其包含成员的平均位置;
  • 然后重新划分其内部成员。

k是算法中的超参数，表示类的数量；k-Means可以自动分配样本到不同的类，但是不能决定究竟要分几个类。

k必须是一个比训练集样本数小的正整数。有时，类的数量是由问题内容指定的。例如，一个鞋厂有三种新款式，它想知道每种新款式都有哪些潜在客户，于是它调研客户，然后从数据里找出三类。也有一些问题没有指定聚类的数量，最优的聚类数量是不确定的。

k-Means的参数是类的重心位置和其内部观测值的位置。与广义线性模型和决策树类似，k-Means参数的最优解也是以代价函数最小化为目标。k-Means代价函数公式如下：
$$
J = \sum_{k=1}^{K} \sum_{i \in C_k} | x_i - u_k|^2
$$

$u_k$是第$k$个类的重心位置，定义为：
$$
u_k = \frac{1}{|C_k|} \sum_{i \in C_k} x_i
$$

成本函数是各个类畸变程度（distortions）之和。每个类的畸变程度等于该类重心与其内部成员位置距离的平方和。若类内部的成员彼此间越紧凑则类的畸变程度越小，反之，若类内部的成员彼此间越分散则类的畸变程度越大。

2. 算法流程

求解成本函数最小化的参数就是一个重复配置每个类包含的观测值，并不断移动类重心的过程。

输入：$T={ x_1, x_2, …, x_N}$，其中$x_i \in R_n$，i=1,2…N

输出：聚类集合$C_k$, 聚类中心$u_k$, 其中k=1,2,…K

  1. 初始化类的重心$u_k$，可以随机选择样本作为聚类中心
  2. 每次迭代的时候，把所有样本分配到离它们最近的类，即更新聚类集合$C_k$
  3. 然后把重心移动到该类全部成员位置的平均值那里，即更新$u_k$
  4. 若达到最大迭代步数，或两次迭代差小于设定的阈值则算法结束，否则重复步骤2

3. 算法实现

K-Means的简单实现如下所示，根据不同情景的需要设计不同的距离函数即可。

def compute_distances(A, B):
    # TODO 根据实际应用场景进行定义
    pass

def K_means(data, K, N):
    """
    KMeans聚类算法的具体实现
    :param data:
    :param K: 聚类的个数
    :param N: 算法的迭代次数
    :return: 类别标志labels与中心坐标centerPoints
    """
    # 获取数据行数
    n = np.shape(data)[0]
    # 从n条数据中随机选择K条，作为初始中心向量
    # centerId是初始中心向量的索引坐标
    centerId = random.sample(range(0, n), K)
    # 获得初始中心向量，共k个
    centerPoints = data[centerId]
    # 计算data到centerPoints的距离矩阵
    # dist[i][:],是i个点到各个中心点的距离
    dist = compute_distances(data, centerPoints)
    # 这里进行第一次判断，距离哪个中心点进就判断为哪一类
    # axis=1寻找每一行中最小值的索引
    labels = np.argmin(dist, axis=1).squeeze()
    # 迭代次数
    count = 0
    # 循环次数小于迭代次数，一直迭代
    while count < N:
        for i in range(K):
            # 重新计算每一个类别的中心点
            centerPoints[i] = np.mean(data[np.where(labels == i)], 0)
        # 重新计算距离矩阵
        dist = compute_distances(data, centerPoints)
        # 重新分类
        labels = np.argmin(dist, axis=1).squeeze()
        # 迭代次数加1
        count += 1
    # 返回类别标识，中心坐标
    return labels, centerPoints

4. 算法应用

比如我们要对下面的数据应用K-Means算法，以此来区分两个圆环：

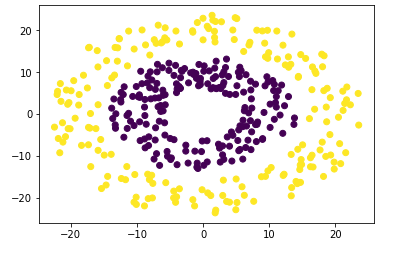
我们可以先进行特征变换，将数据从每一个点的坐标(x, y)变换为点到原点的距离disc，这样我们就可以更方便的区分这两个圆环：

# 进行特征变化，这里很容易想到将特征变化为点到原点的距离（这里用的平方）
trans_data = np.array([train_data[0] ** 2 + train_data[1] ** 2])

之后我们构造下面这样的距离函数：

def compute_distances(A, B):
    """
    计算两组向量之间的距离，两个向量要有一样的维度和长度
    """
    # 与sqrt(sum(power(vecA - vecB, 2)))相比，这个可以直接计算一整组的距离，更方便
    return cdist(A, B, metric="euclidean")

这样就可以应用上面实现的K-Means算法了。

注：

该部分的数据自己随机生成即可，如果不会生成，可以使用这个网址上的数据：https://github.com/Immortalqx/ML_Homework/blob/master/homework_03_kmeans/dataset_circles.csv

完整代码

import time
import numpy as np
import random
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist


def compute_distances(A, B):
    """
    计算两组向量之间的距离，两个向量要有一样的维度和长度
    """
    # 与sqrt(sum(power(vecA - vecB, 2)))相比，这个可以直接计算一整组的距离，更方便
    return cdist(A, B, metric="euclidean")


def K_means(data, K, N):
    """
    KMeans聚类算法的具体实现
    :param data:
    :param K: 聚类的个数
    :param N: 算法的迭代次数
    :return: 类别标志labels与中心坐标centerPoints
    """
    # 获取数据行数
    n = np.shape(data)[0]
    # 从n条数据中随机选择K条，作为初始中心向量
    # centerId是初始中心向量的索引坐标
    centerId = random.sample(range(0, n), K)
    # 获得初始中心向量，共k个
    centerPoints = data[centerId]
    # 计算data到centerPoints的距离矩阵
    # dist[i][:],是i个点到各个中心点的距离
    dist = compute_distances(data, centerPoints)
    # 这里进行第一次判断，距离哪个中心点进就判断为哪一类
    # axis=1寻找每一行中最小值的索引
    labels = np.argmin(dist, axis=1).squeeze()
    # 迭代次数
    count = 0
    # 循环次数小于迭代次数，一直迭代
    while count < N:
        for i in range(K):
            # 重新计算每一个类别的中心点
            centerPoints[i] = np.mean(data[np.where(labels == i)], 0)
        # 重新计算距离矩阵
        dist = compute_distances(data, centerPoints)
        # 重新分类
        labels = np.argmin(dist, axis=1).squeeze()
        # 迭代次数加1
        count += 1
    # 返回类别标识，中心坐标
    return labels, centerPoints


def evaluate(data, labels):
    """
    评估聚类的结果
    """
    num, div = np.shape(data)
    # 判断数据的维度是不是1
    if div != 1:
        print("sorry,the dimension of your dataset is not 1!")
        return 1

    count = 0
    for i in range(num):
        if data[i] == labels[i]:
            count += 1
        i += 1
    score = count * 1.0 / num
    # 因为分类是随机的，不一定对应的上（比如0和1对应，1和0对应，导致正确率为0），所以要调整一下
    if 1 - score > score:
        score = 1 - score
    print("score = %f" % (100.0 * score))


def getCenterPoint(data, K, labels):
    centerPoints = data[:K]
    for i in range(K):
        # 重新计算每一个类别的中心点
        centerPoints[i] = np.mean(data[np.where(labels == i)], 0)
    return centerPoints


def plotFeature(data, labels_, centerPoints):
    """
    二维空间显示聚类结果
    """
    # 获取簇集的个数
    clusterNum = len(set(labels_))
    # 内定的颜色种类
    scatterColors = ["orange", "purple", "cyan", "red", "green"]

    # 判断数据的维度是不是２
    if np.shape(data)[1] != 2:
        print("sorry,the dimension of your dataset is not 2!")
        return 1
    # 判断簇集类别是否大于５类
    if clusterNum > len(scatterColors):
        print("sorry,your k is too large,please add length of the scatterColors!")
        return 1

    # 散点图的绘制
    for i in range(clusterNum):
        colorSytle = scatterColors[i % len(scatterColors)]
        subCluster = data[np.where(labels_ == i)]
        plt.scatter(subCluster[:, 0], subCluster[:, 1], c=colorSytle, s=20)

    # 中心点的绘制
    mark = ["*", "^", "o", "X", "D"]  # 这个是设置绘制的形状
    label = ["0", "1", "2", "3", "4"]  # label的作用是设置图例
    c = ["blue", "red", "peru", "violet", "black"]
    for i in range(clusterNum):
        plt.plot(centerPoints[i, 0], centerPoints[i, 1],
                 mark[i], markersize=15, label=label[i], c=c[i])
        plt.legend(loc="upper left")  # 图例

    # 设置x、y轴和标题
    plt.xlabel("x-label")
    plt.ylabel("y-label")
    plt.title("k-means cluster result")

    plt.show()


if __name__ == "__main__":
    # 用户定义聚类数
    K = 2
    # 从文本中加载数据
    data = np.loadtxt("../dataset_circles.csv", delimiter=",")
    # 分割前两列作为训练集
    train_data = data.T[0:2]
    # 进行特征变化，这里很容易想到将特征变化为点到原点的距离（这里用的平方）
    trans_data = np.array([train_data[0] ** 2 + train_data[1] ** 2])
    # 分割第三列作为测试集
    test_data = data.T[2:3]
    # 开始计时
    start = time.clock()
    # 执行KMeans算法
    labels, _ = K_means(trans_data.T, K, 30)
    # 结束计时
    end = time.clock()
    # 由于这里进行特征变化了，返回的中心点是一维的，因此要根据聚类结果重新计算中心点
    centerPoints = getCenterPoint(train_data.T, K, labels)
    # 评估聚类算法的结果
    evaluate(test_data.T, labels)
    # 输出聚类算法所用时间
    print("time = %s" % str(end - start))
    # 绘图显示
    plotFeature(train_data.T, labels, centerPoints)
文章作者: Immortalqx
文章链接: http://Immortalqx.github.io/2022/01/07/machine-learning-1/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Immortalqx !
K-Means 机器学习
赏
评论
  目录