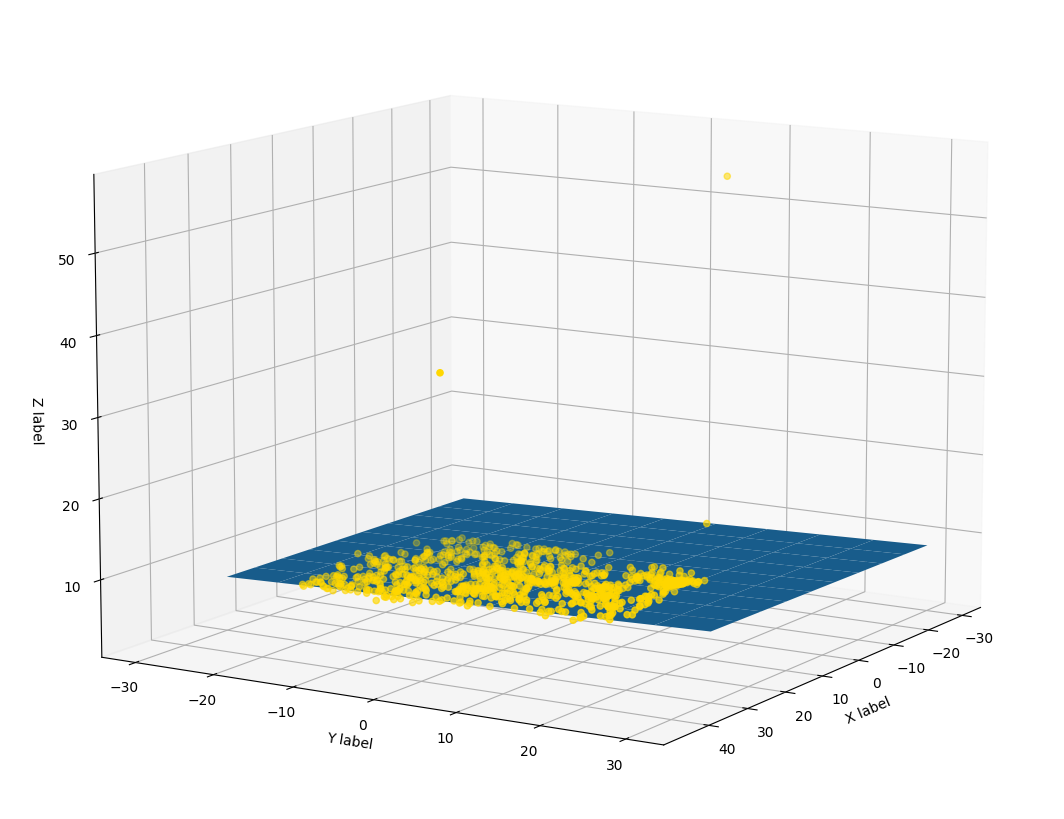
使用RANSAC算法拟合点云中的平面
最近在写pi-slam-fusion这个项目,需要根据pi-slam计算出来的点云拟合出大地平面的方程,从而让map2dfusion根据这个方程进行地图拼接。
这一步我使用了ransac算法,并且对ransac算法进行了一点总(ban)结(yun)。
RANSAC简介
RANSAC(RAndom SAmple Consensus,随机采样一致)算法是从一组含有“外点”(outliers)的数据中正确估计数学模型参数的迭代算法。
“外点”一般指的的数据中的噪声,比如说匹配中的误匹配和估计曲线中的离群点。所以,RANSAC也是一种“外点”检测算法。RANSAC算法是一种不确定算法,它只能在一种概率下产生结果,并且这个概率会随着迭代次数的增加而加大。RANSAC算最早是由Fischler和Bolles在SRI上提出用来解决LDP(Location Determination Proble)问题的。
RANSAC的基本假设
- “内群”(inlier, 似乎译为内点群更加妥当,即正常数据,正确数据)数据可以通过几组模型的参数来叙述其分布,而“离群”(outlier,似乎译为外点群更加妥当,异常数据)数据则是不适合模型化的数据。
- 数据会受噪声影响,噪声指的是离群,例如从极端的噪声或错误解释有关数据的测量或不正确的假设。
- RANSAC假定,给定一组(通常很小)的内点群,存在一个程序,这个程序可以估算最佳解释或最适用于这一数据模型的参数。
范例
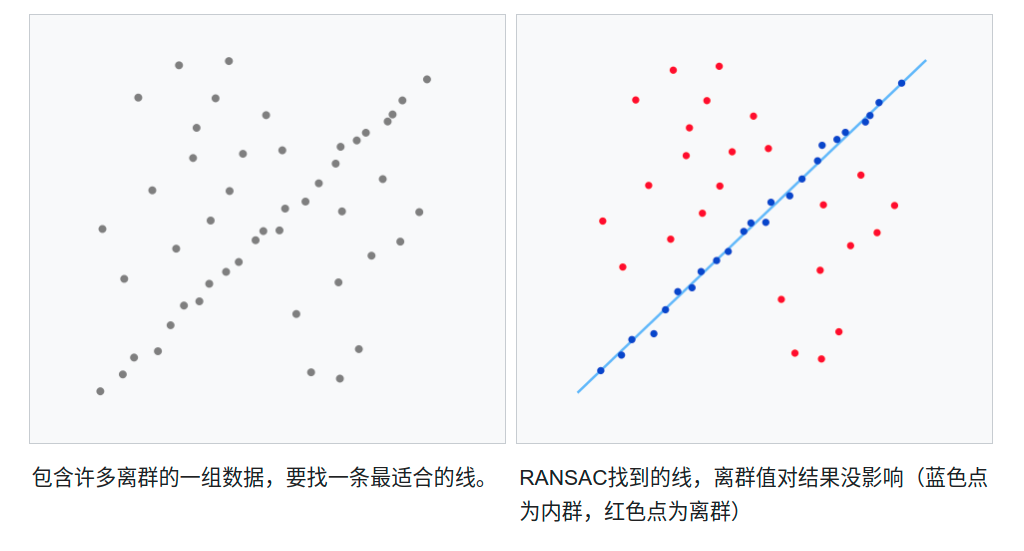
这里用一个简单的例子来说明,在一组数据点中找到一条最适合的线。假设,此有一组集合包含了内点群以及外点群,其中内点群包含可以被拟合到线段上的点,而外点群则是无法被拟合的点。如果我们用简单的最小二乘法来找此线,我们将无法得到一条适合于内点群的直线,因为最小二乘法会受外点群影响而影响其结果。而用RANSAC,可以只由内点群来计算出模型,而且概率还够高。然而,RANSAC无法保证结果一定最好,所以必须小心选择参数,使其能有足够的概率。
算法基本思想和流程
RANSAC是通过反复选择数据集去估计出模型,一直迭代到估计出认为比较好的模型。
具体的实现步骤可以分为以下几步:
- 选择出可以估计出模型的最小数据集;(对于直线拟合来说就是2个点,对于平面拟合就是3个点)
- 使用这个数据集来计算出数据模型;
- 将所有数据带入这个模型,计算出“内点”的数目;(累加在一定误差范围内的适合当前迭代推出模型的数据)
- 比较当前模型和之前推出的最好的模型的“内点“的数量,记录最大“内点”数的模型参数和“内点”数;
- 重复1-4步,直到迭代结束或者当前模型已经足够好了(“内点数目大于一定数量”)。
编程实现
以RANSAC算法拟合点云中的平面为例,介绍python实现的核心代码。
求解平面方程
这里是根据最小数据集(点A、点B、点C)来计算数据模型(平面方程)的过程,对应上面的1、2步
def solve_plane(A, B, C):
"""
求解平面方程
:param A: 点A
:param B: 点B
:param C: 点C
:return: Point(平面上一点),Quaternion(平面四元数),Nx(平面的法向量)
"""
# 两个常量
N = np.array([0, 0, 1])
Pi = 3.1415926535
# 计算平面的单位法向量,即BC 与 BA的叉积
Nx = np.cross(B - C, B - A)
Nx = Nx / np.linalg.norm(Nx)
# 计算单位旋转向量与旋转角(范围为0到Pi)
Nv = np.cross(Nx, N)
angle = acos(np.dot(Nx, N))
# 考虑到两个向量夹角不大于Pi/2,这里需要处理一下
if angle > Pi / 2.0:
angle = Pi - angle
Nv = -Nv
# FIXME: 此处如何确定平面上的一个点???
# Point = (A + B + C) / 3.0
Point = B
# 计算单位四元数
Quaternion = np.append(Nv * sin(angle / 2), cos(angle / 2))
# print("旋转向量:\t", Nv)
# print("旋转角度:\t", angle)
# print("对应四元数:\t", Quaternion)
return Point, Quaternion, Nx计算点到平面的距离
我们可以根据点到平面的距离来判断这个点是否为内点。
def solve_distance(M, P, N):
"""
求解点M到平面(P,Q)的距离
:param M: 点M
:param P: 平面上一点
:param N: 平面的法向量
:return: 点到平面的距离
"""
# 从四元数到法向量
# A = 2 * Q[0] * Q[2] + 2 * Q[1] * Q[3]
# B = 2 * Q[1] * Q[2] - 2 * Q[0] * Q[3]
# C = -Q[0] ** 2 - Q[1] ** 2 + Q[2] ** 2 + Q[3] ** 2
# D = -A * P[0] - B * P[1] - C * P[2]
# 为了计算简便,直接使用求解出的法向量
A = N[0]
B = N[1]
C = N[2]
D = -A * P[0] - B * P[1] - C * P[2]
return fabs(A * M[0] + B * M[1] + C * M[2] + D) / sqrt(A ** 2 + B ** 2 + C ** 2)
通过RANSAC算法进行拟合
这里是RANSAC算法的主要实现过程。
下面的函数计算出的P是平面上的一点,Q是平面的四元数,N是平面的法向量。
def RANSAC(data):
"""
使用RANSAC算法估算模型
"""
# 数据规模
SIZE = data.shape[0]
# 迭代最大次数,每次得到更好的估计会优化iters的数值,默认10000
iters = 10000
# 数据和模型之间可接受的差值,默认0.25
sigma = 0.15
# 内点数目
pretotal = 0
# 希望的得到正确模型的概率,默认0.99
Per = 0.999
# 初始化一下
P = np.array([])
Q = np.array([])
N = np.array([])
for i in range(iters):
# 随机在数据中选出三个点去求解模型
sample_index = random.sample(range(SIZE), 3)
P, Q, N = solve_plane(data[sample_index[0]], data[sample_index[1]], data[sample_index[2]])
# 算出内点数目
total_inlier = 0
for index in range(SIZE):
if solve_distance(data[index], P, N) < sigma:
total_inlier = total_inlier + 1
# 判断当前的模型是否比之前估算的模型好
if total_inlier > pretotal:
iters = log(1 - Per) / log(1 - pow(total_inlier / SIZE, 2))
pretotal = total_inlier
# 判断是否当前模型已经符合超过一半的点
if total_inlier > SIZE / 2:
break
return P, Q, N运行项目
具体的代码(包括C++实现和python实现)都放在https://github.com/Immortalqx/RANSAC.git
你可以通过下面的指令运行这篇博客介绍的RANSAC算法。
克隆本项目:
git clone https://github.com/Immortalqx/RANSAC.git运行C++部分的代码:
cd RANSAC
mkdir build
cd build
cmake ..
make
./RANSAC运行python部分的代码:
#在平面中用ransac算法拟合直线
python3 RANSAC_2D.py
#在点云中用ransac算法拟合平面
python3 RANSAC_3D.py运行结果:
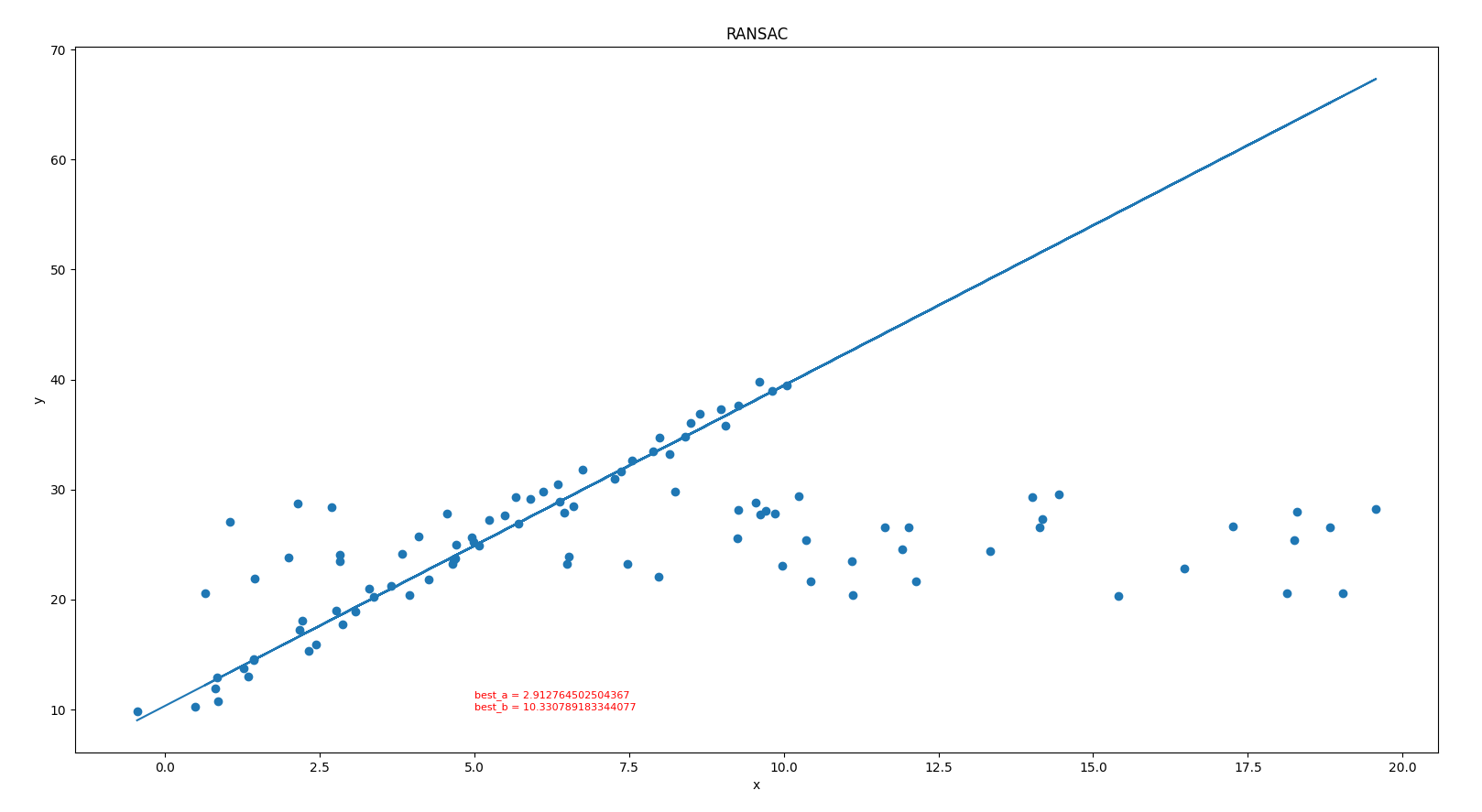
对2D平面中的直线进行拟合
对点云中的平面进行拟合