Harris角点检测原理
Harris角点最早在paper A Combined Corner and Edge Detector中被Chris Harris & Mike Stephens提出。
0、Harris角点检测的基本思想:
算法基本思想是使用一个固定窗口在图像上进行任意方向上的滑动,比较滑动前与滑动后两种情况,窗口中的像素灰度变化程度,如果存在任意方向上的滑动,都有着较大灰度变化,那么我们可以认为该窗口中存在角点。
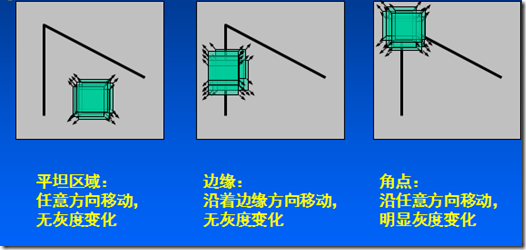
1、灰度变化描述
当窗口发生$ [u,v] $移动时,那么滑动前与滑动后对应的窗口中的像素点灰度变化描述如下:
$$
E(u,v)=\sum\limits_{(x,y)€W}w(x,y)[I(x+u,y+v)-I(x,y)]^2
$$
其中
- $[u,v]$是窗口$W$的偏移量;
- $(x,y)$是窗口$W$所对应的像素坐标位置,窗口有多大,就有多少个位置;
- $I(x,y)$是像素坐标位置$(x,y)$的图像灰度值;
- $I(x+u,y+v)$是像素坐标位置$(x+u,y+v)$的图像灰度值;
- $w(x,y)$是窗口函数,最简单情形就是窗口$W$内的所有像素所对应的$w$权重系数均为1.但有时候,我们会将$w(x,y)$函数设置为以窗口$W$中心为原点的二元正太分布。如果窗口$W$中心点是角点时,移动前与移动后,该点在灰度变化贡献最大;而离窗口$W$中心(角点)较远的点,这些点的灰度变化几近平缓,这些点的权重系数,可以设定小值,以示该点对灰度变化贡献较小,那么我们自然而然想到使用二元高斯函数来表示窗口函数;
根据上述表达式,当窗口在平坦区域上移动灰度不会发生什么变换。如果窗口处在纹理比较丰富的区域上滑动,那么灰度变化会很大。
算法最终思想就是计算灰度发生较大变化时所对应的位置,当然这个较大是指任意方向上的滑动,并非单指某个方向。
2、 $E(u,v)$化简
根据泰勒公式:
$$
f(x+u,y+v)≈f(x,y)+uf_x(x,y)+vf_y(x,y)
$$
我们可以将上面的公式化简为:
$$
\sum\limits_{(x,y)€W}w(x,y)[I(x+u,y+v)-I(x,y)]^2\\
≈\sum\limits_{(x,y)€W}w(x,y)[I(x,y)+uI_x+vI_y-I(x,y)]^2\\
=\sum\limits_{(x,y)€W}w(x,y)[u^2I_x^2+2uvI_xI_y+v^2I_y^2]\\
=\sum\limits_{(x,y)€W}w(x,y)\begin{bmatrix}u & v\end{bmatrix}\begin{bmatrix} I_x^2 & I_xIy \ I_xI_y & I_y^2\end{bmatrix}\begin{bmatrix}u \ v\end{bmatrix}\\
=\begin{bmatrix}u & v\end{bmatrix}(\sum\limits_{(x,y)€W}w(x,y)\begin{bmatrix} I_x^2 & I_xIy \ I_xI_y & I_y^2\end{bmatrix})\begin{bmatrix}u \ v\end{bmatrix}
$$
所以$E(u,v)$表达式可以更新为:
$$
E(u,v)=\begin{bmatrix}u & v\end{bmatrix}M\begin{bmatrix}u \ v\end{bmatrix}
$$
其中:$M=\sum\limits_{(x,y)€W}w(x,y)\begin{bmatrix} I_x^2 & I_xIy \ I_xI_y & I_y^2\end{bmatrix}$,
$I_x$,$I_y$分别为窗口内像素点$(x,y)$在$x$方向上和$y$方向上的梯度值。
3、矩阵$M$的关键性
Harris角点检测算法并不是直接根据$E(u,v)$来判断角点的,而是通过对窗口内的每个像素的$x$方向上的梯度与$y$方向上的梯度进行统计分析。假设我们这里以$I_x$和$I_y$为坐标轴,则每个像素的梯度坐标可以表示成$(I_x,I_y)$。
针对平坦区域,边缘区域以及角点区域三种情形进行分析:

下图是对这三种情况窗口中的对应像素的梯度分布进行绘制:
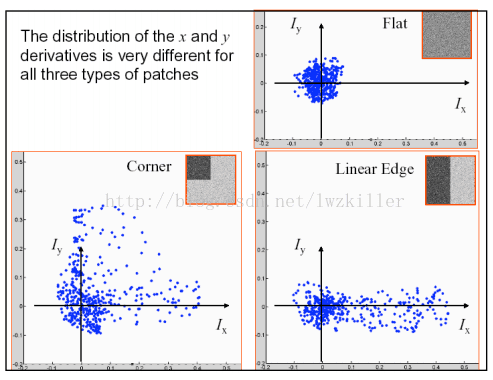
我们可以很明显的看出这三种区域的特点:
平坦区域上的每个像素点所对应的$(I_x,I_y)$坐标分布在原点附近。
其实也很好理解:针对平坦区域的像素点,他们的梯度方向虽然各异,但是其幅值都不是很大,所以均聚集在原点附近。
边缘区域有一坐标轴分布较散。
至于是哪一个坐标上的数据分布较散不能一概而论,这要视边缘在图像上的具体位置而定,如果边缘是水平或者垂直方向,那么$I_y$轴方向或者$I_x$方向上的数据分布就比较散;
角点区域的$I_x$、$I_y$方向上的梯度分布都比较散。
所以,我们可以尝试利用这些特征来判断哪些区域存在角点。
之前我们已经计算出了$M$矩阵:
$$
M=
\sum\limits_{(x,y)€W}w(x,y)\begin{bmatrix} I_x^2 & I_xIy \ I_xI_y & I_y^2\end{bmatrix}=
\begin{bmatrix} A & C \ C & B \end{bmatrix}
$$
我们可以把$E(u,v)$近似为二项函数:$E(u,v)=Au^2+2Cuv+Bv^2$
其中:
$$
A=\sum\limits_{(x,y)€W}w(x,y)*I_x^2\
B=\sum\limits_{(x,y)€W}w(x,y)*I_y^2\
C=\sum\limits_{(x,y)€W}w(x,y)*I_xI_y
$$
二次项函数本质上就是一个椭圆函数。椭圆的长和宽是由$M$的特征值$λ1,λ2$决定的(椭圆的长短轴正是矩阵$M$特征值平方根的倒数),椭圆的方向是由$M$的特征向量决定的,椭圆方程为:
$$
\begin{bmatrix} u & v \end{bmatrix}M\begin{bmatrix} u \ v \end{bmatrix}=1
$$
如果使用椭圆进行数据集表示,则绘制图示如下:
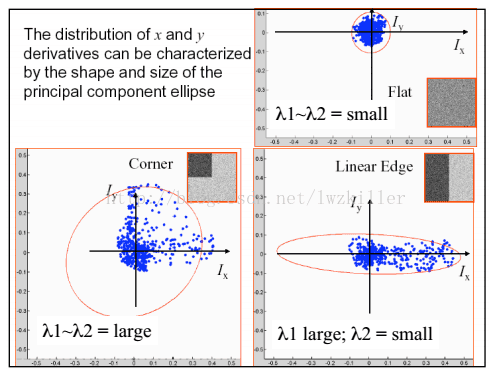
从上图中我们可以看出:
- 如果$λ1,λ2$都很大,并且很接近,就可以认为是一个角点
- 如果$λ1,λ2$中只有一个值大,那么这只是一个边缘,不是角点
- 如果$λ1,λ2$很接近但是数值比较小,那么这里就是一个平坦区域
4、角点响应的度量
通常用下面表达式进行度量,对每一个窗口计算得到一个分数$R$,根据$R$的大小来判定窗口内是否存在harris特征角点。分数$R$根据下面公式计算得到:
$$
R=det(M)-k(trace(M))^2\
det(M)=λ_1λ_2\
trace(M)=λ_1+λ_2
$$
这里$λ1,λ2$是矩阵$M$的2个特征值,$k$是一个指定值,这是一个经验参数,需要实验确定它的合适大小,通常它的值在0.04和0.06之间,它的存在只是调节函数的形状而已。
$R$取决于$M$的特征值,对于角点$|R|$很大,平坦的区域$|R|$很小,边缘的$R$为负值;
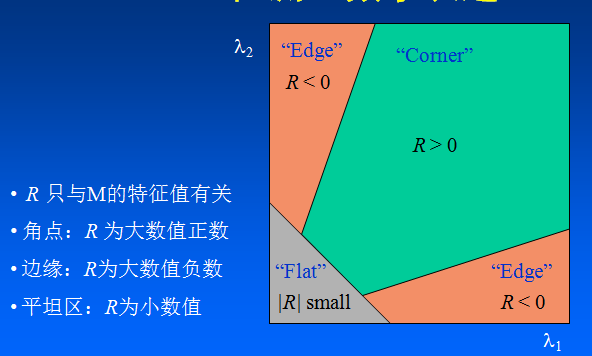
最后设定R的阈值,进行角点判断即可。



