2D碰撞检测

2D游戏中，通常使用矩形、圆形等来代替复杂图形的相交检测，因为这两种形状的碰撞检测速度是最快的。

其中矩形包围盒又可以分为轴对齐包围盒（AABB, Axis Aligned Bounding Box）与转向包围盒（OBB, Oriented Bounding Box）。AABB与OBB的区别在于，AABB中的矩形的其中一条边和坐标轴平行，OBB的计算复杂度要高于AABB。根据不同的使用场景，可以用不同的方案。

圆形之间的碰撞检测

圆形之间的碰撞检测比较简单，只需判断两圆心之间的距离是否小于两圆的半径之和即可，如下图所示。

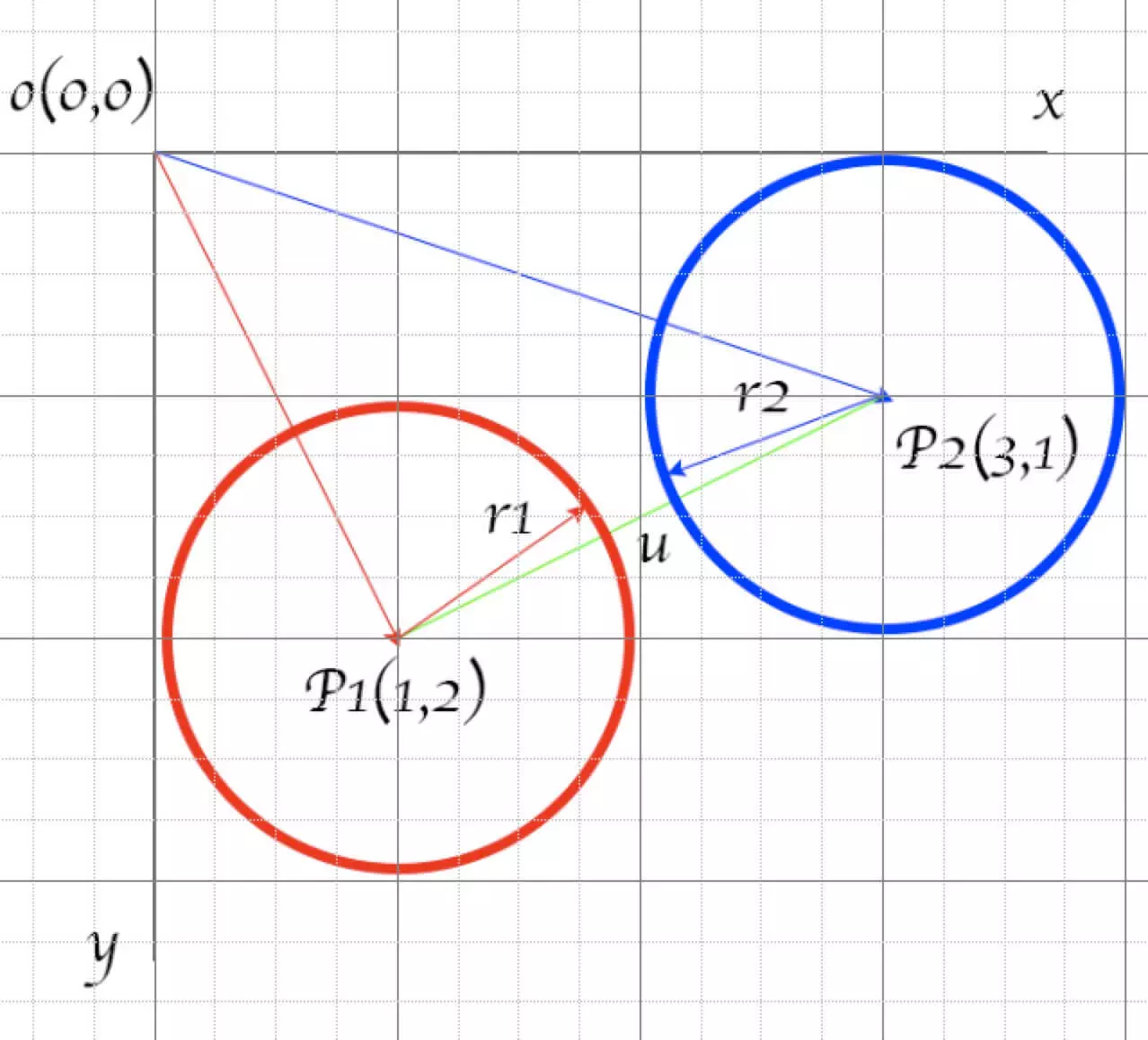
圆形与矩形的碰撞检测

涉及到矩形的碰撞检测问题都先要判断是否轴对称。

矩形轴对称

如下图所示，设$c$为矩形中心，$h$为矩形半长，$p$为圆心，$r$为半径。

检测碰撞的方法是计算圆心与矩形的最短距离$ u$，若$ u $的长度小于$ r $则两者相碰撞。

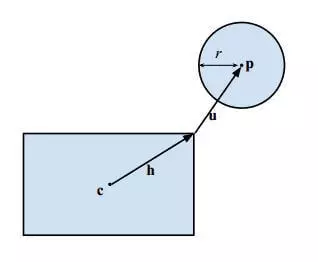
为了计算$u$，我们首先利用$p – c$ 将圆心平移到矩形坐标系的第一象限，这不影响碰撞检测的结果：

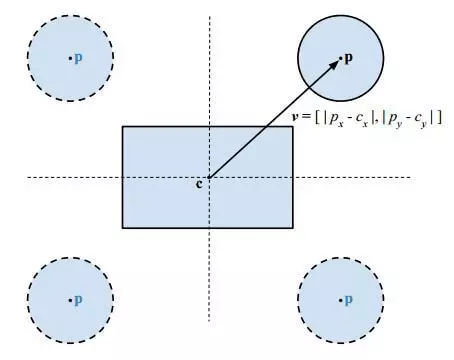
然后，计算向量 $v-h$，如果$v-h$的分量为负数则设置为0，最后得到圆心与矩形最短距离的矢量 $u$。

下图展示了4种情况，红色的$u$是结果。

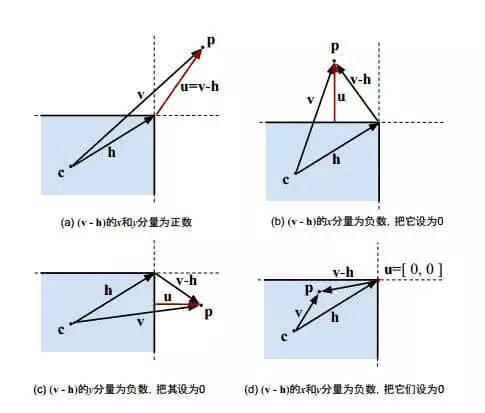
最后比较 $u$ 和 $r$ 模长的大小，如果$u$的模长小则两者相交。

矩形非轴对称

将矩形的中心视为旋转中心，将矩形和圆形一起反向旋转将矩形转为轴对称，然后就可以套用上面的解法。

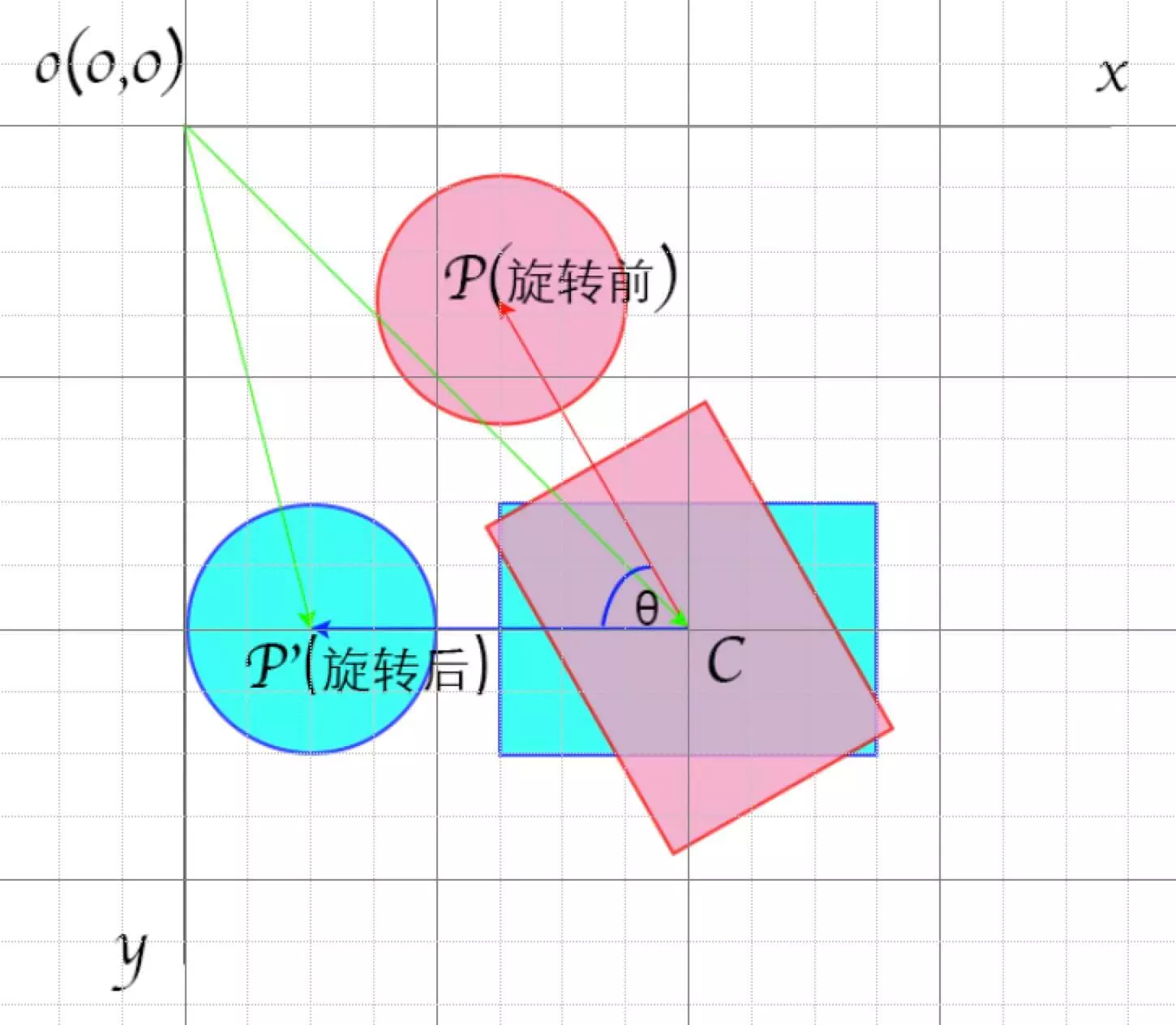
两矩形都轴对称AABB

想象一下两个矩形A和B，B紧贴着A的边走了一圈，B的矩形中心的轨迹是一个新的矩形，这样就简化成新矩形与B中心点这一点的相交问题，又因为点可以看成是半径为0的圆，所以问题又转换为圆形和矩形相交。

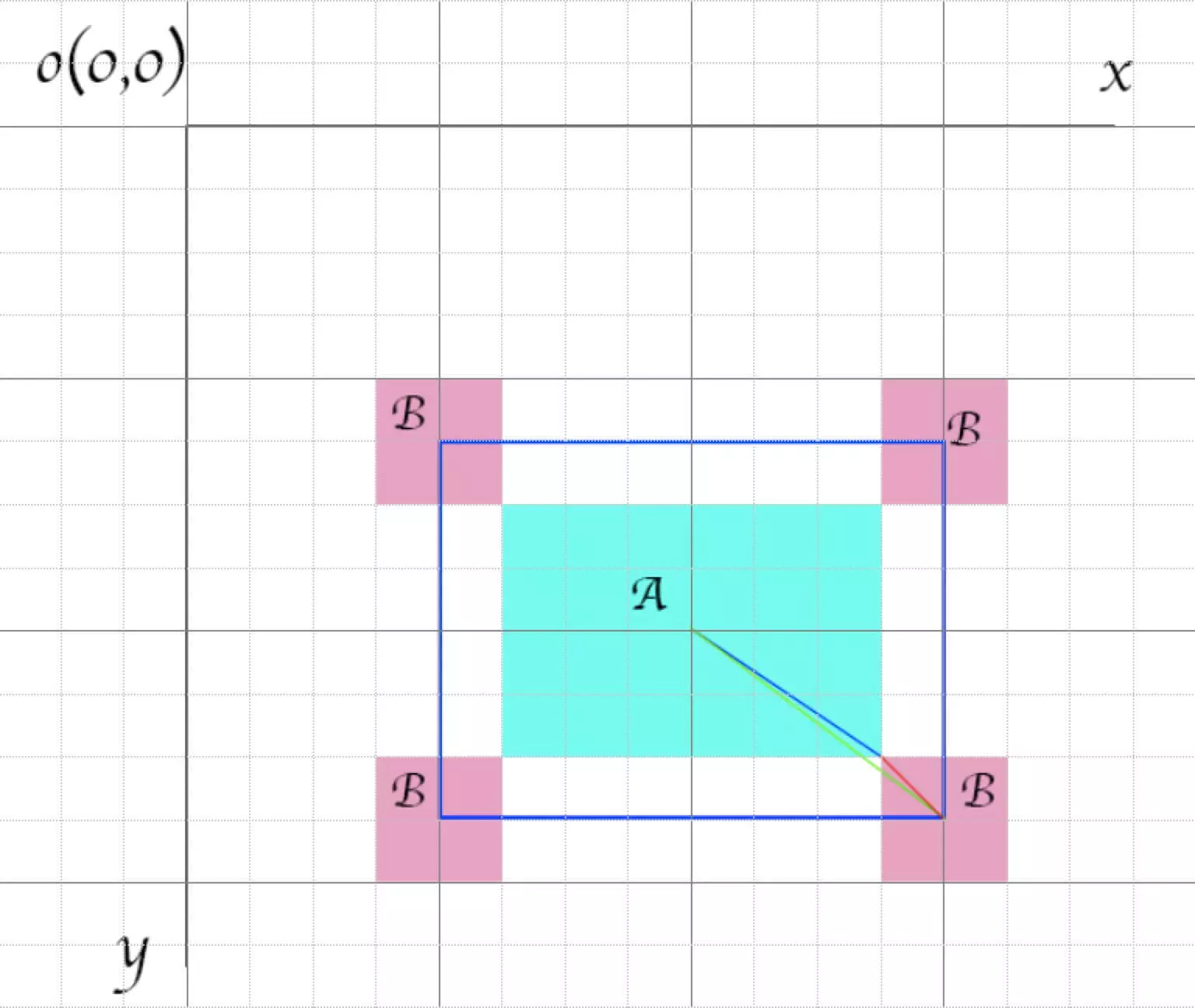
两矩形相交非轴对称OBB

两个矩形的OBB检测使用分离轴定理（Separating Axis Theorem）

分离轴定理：通过判断任意两个矩形在任意角度下的投影是否均存在重叠，来判断是否发生碰撞。若在某一角度光源下，两物体的投影存在间隙，则为不碰撞，否则为发生碰撞。

因为矩形的对边平行，所以只要判断四条对称轴上两个矩阵的投影即可。如果四条对称轴上的投影均有重合部分，则矩阵发生碰撞，否则矩阵之间不发生碰撞。