SLAM问题的数学表述

本文是作者对于SLAM问题数学表述的一些理解，如有错误，非常非常非常欢迎指正！

经典SLAM模型

经典SLAM模型由一个运动方程和一个观测方程构成，如下所示：
$$
\begin{cases}
x_k &= \ f(x_{k-1},u_k,w_k) \\
z_{k,j} &= \ h(y_j,x_k,v_{k,j})
\end{cases}
$$
有时候也会写成下面这样的形式：
$$
\begin{cases}
x_k &= \ f(x_{k-1},u_k) +w_k \\
z_{k,j} &= \ h(y_j,x_k)+v_{k,j}
\end{cases}
$$
这两种形式本质上都是一样的。其中，$ x_k $表示第k次的位置或者位姿，$ u_k $表示第k次传感器的读数或者输入，$ w_k $表示第k次运动过程中的噪声；而$ y_j $为观测到的路标点j，$ z_{k,j} $则表示第k次观测中对于路标点j所得到的观测结果，$ v_{k,j} $为本次观测过程中的噪声。而上面的函数 $ f $ 和 $ h $ ，需要根据具体的情况来确定。

之后，我们将以视觉SLAM为例来更深入的理解SLAM的数学表述。

针孔相机模型

考虑到视觉SLAM的传感器是相机，并且通常符合针孔相机模型。所以在继续探讨之前，我们将对针孔相机模型做一个简单的介绍。

从相机坐标系到图像坐标系

如下图，相机坐标系下的一点$ P(X, Y, Z) $，通过小孔成像在相机的物理成像平面上，记为$ P’(X’, Y’) $。

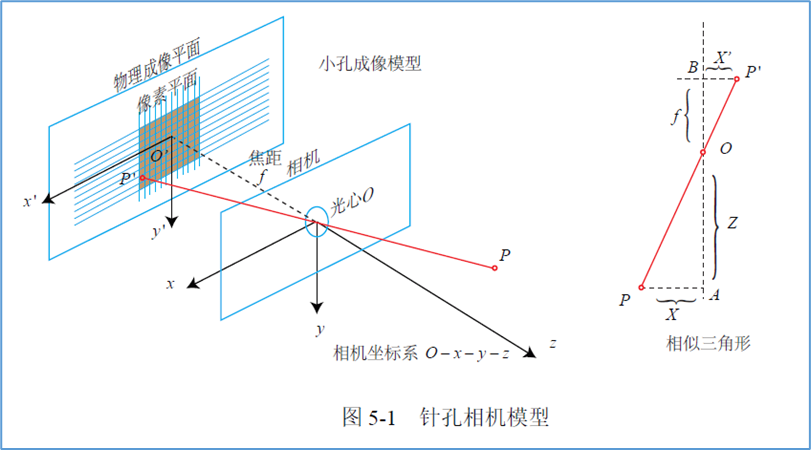
我们能够很容易的得出以下结论：
$$
\frac Zf=- \frac X{X’}=- \frac Y{Y’}
$$
由于我们通常看到的像都是正的，并且为了公式的简洁，我们对上式加以整理，得到：
$$
X’=f \frac XZ \\
Y’=f \frac YZ
$$

从图像坐标系到像素坐标系

事实上，计算机看到的图像都是由像素构成的，从图像坐标系到像素坐标系还需要经过一次转化。这里我们记像素坐标为$ P’’(u,v) $。
$$
\begin{cases}
u=\alpha X’+c_x \\
v=\beta Y’+c_y
\end{cases}
$$
其中$ \alpha $和$ \beta $分别表示x轴和y轴的缩放系数，而$ c_x $和$ c_y $则表示平移量。

我们将之前得到的结论代入上式，可以得到：
$$
\begin{cases}
u=f_x\frac XZ+c_x \\
v=f_y\frac YZ+c_y
\end{cases}
$$
其矩阵形式可以表示为：
$$
\begin{pmatrix} u\\v\\1 \end{pmatrix}=\frac1Z\begin{pmatrix}f_x & 0 & c_x \\ 0 & f_y & c_y\\0 & 0 & 1 \end{pmatrix}
\begin{pmatrix}X\\Y\\Z\end{pmatrix}
\overset{\text{def}}{=}\frac 1ZKP
$$
但我们通常使用下面的公式来表示，它看上去更简洁：
$$
Z\begin{pmatrix} u\\v\\1 \end{pmatrix}=\begin{pmatrix}f_x & 0 & c_x \\ 0 & f_y & c_y\\0 & 0 & 1 \end{pmatrix}
\begin{pmatrix}X\\Y\\Z\end{pmatrix}
\overset{\text{def}}{=}KP
$$
左边的是齐次坐标，而右边的是非齐次坐标。我们把中间的矩阵称为内参数，记为K，内参通常在相机生产之后就已经固定，我们可以通过查询或者标定获得相机的内参。

从世界坐标系到相机坐标系

上面我们仅仅描述了物体从相机坐标系到像素坐标系的转化。而在SLAM中，我们通常需要设置一个世界坐标系以描述相机或机器人的位置信息。因此从物体被观测，再到获得观测结果，即物体的像素坐标，中间还有一个转化过程。我们使用如下的一个式子进行描述：
$$
ZP_{uv}=Z\begin{pmatrix} u\\v\\1 \end{pmatrix}=KP=K(RP_w+t)=KTP_w
$$
这里，$ R $是旋转矩阵，$ t $是平移矩阵，$ T= \begin{pmatrix} R & t \\ 0 & 1 \end{pmatrix} $。可以理解为使用世界坐标系描述的点$ P_w $经过旋转变化和平移变化，得到了使用相机坐标系描述的点$ P $。

其中R，t 或T被称为外参，而外参正是SLAM估计的目标。

更具体的数学表述

再回到最开始提到的运动方程和观测方程：
$$
\begin{cases}
x_k &= \ f(x_{k-1},u_k) +w_k \\
z_{k,j} &= \ h(y_j,x_k)+v_{k,j}
\end{cases}
$$

我们知道机器人有六个自由度，因此我们可以把$ x_k $理解为第k次观测时机器人的位姿，它是六维的，我们可以用向量表示，也可以使用变换矩阵表示，即上面的$ T $（可以认为当前机器人的位姿是由机器人在原点经过$ R $旋转和$ t $平移得到的）。此时运动方程描述的是机器人在第k-1次观测后，对其传感器输入$ u_k $，使机器人的位姿从$ x_{k-1} $变换到了$ x_k $，而$ w_k $则是此次运动中的噪声。

而我们上面讲的针孔相机模型，实际上就是视觉SLAM中的观测模型。公式中$ y_j $就是针孔相机模型中我们观测的点$ P_w $，表示世界坐标系下路标点j的坐标，而$ z_{k,j} $就是观测的最终结果——像素坐标$ P_{uv} $。$ x_k $既是机器人的位姿，实际上也是模型中的外参$ T $。$ v_{k,j} $则是此次观测中的噪声。

至此，我们可以用一种更具体的形式重写上面的运动方程和观测方程：
$$
\begin{cases}
T_k &= \ f(T_{k-1},u_k) +w_k \\
s_j P_{uv(k,j)} &= \ K(R_kP_{w(j)}+t_k)+v_{k,j}=KT_kP_{w(j)}+v_{k,j}
\end{cases}
$$
其中$ s_j $是路标点j到相机光心的距离。